基于新近似算法的WSN生命周期优化

通过基于一种新近似算法的数据传播模型延长传感器网络的生命周期

Ramin Yarinezhad， Seyed Naser Hashemi ∗
数学与计算机科学系，德黑兰，伊朗，阿米尔卡比尔科技大学

摘要

将传感器节点分组为簇可以提高无线传感器网络（WSN）的整体可扩展性和网络生命周期。在聚类无线传感器网络中，簇头（CHs）承受的流量负载比普通传感器节点更大，因为它们不仅要收集其簇内所有传感器节点的数据，还要对数据进行聚合并发送到称为汇聚节点的基站。由于这种额外的流量负载，簇头比普通传感器节点更早耗尽能量而失效，因此最小化簇头的负载是一个重要的问题，被称为负载均衡聚类问题（LBCP）。本文提出了一种基于簇的无线传感器网络路由协议。该协议采用具有1.1近似因子的fpt‐近似算法来解决LBCP问题，这意味着其精度显著高于此前报道的该问题的近似因子。提出的协议使用一种能量感知路由算法，以找到将簇头连接到汇聚节点的最优路由树。该路由算法规定了将数据传输到汇聚节点的特定路径，并在特定时间改变这些路径，以平衡节点的能量消耗并延长网络生命周期。仿真结果表明，与多种其他类似协议相比，提出的协议具有更好的性能。
© 2020年 Elsevier B.V.保留所有权利。

1. 引言

微电子机械系统（MEMS）和无线通信技术的最新发展推动了低成本低功耗传感设备的显著进步，并促进了无线传感器网络（WSNs）[1]的发展。无线传感器网络由大量被称为传感器节点的小型设备组成，这些设备被随机部署在特定区域。传感器节点包含传感、计算和通信组件，其主要任务是观测该区域内的事件，并将感知数据传输到基站（或汇聚节点）[2]。无线传感器网络具有广泛的应用，包括灾害管理、安全监控、工业监测、医疗健康监测以及军事应用[2–5]。传感器节点在能量、通信范围、存储和计算资源方面存在限制[6]。此外，传感器节点可能被部署在恶劣且难以到达的环境中，导致无法为其充电或更换电池。在设计这些网络的路由算法时，必须考虑传感器节点的能量限制、短通信范围以及其他限制因素[7]。

∗通讯作者。电子邮件地址： yarinezhad@aut.ac.ir （R. 亚里内扎德），nhashemi@aut.ac.ir （S.N. 哈希米）。

许多研究针对无线传感器网络（WSNs）中的路由问题展开，并提出了多种类型的路由算法，如平面型、聚类、分层和基于位置的算法。这些研究表明，与其它方法相比，基于簇的路由协议在提高无线传感器网络的可扩展性和生命周期方面更为成功[8–12]。在聚类协议中，传感器节点被划分为多个簇，每个簇包含一个簇头（CH）。基于簇的路由协议中的网络操作按轮次进行。每一轮中，首先选择簇头（CH），然后簇头从其簇成员收集数据并发送至汇聚节点。图1展示了一个聚类无线传感器网络。在聚类协议中，每一轮可分为三个阶段：簇头选择、簇形成和数据传输。

在簇头选择阶段，从节点中选出一个最优子集作为簇头。如果簇头是从普通传感器节点中选取的，由于需要接收其簇成员感知的数据、对这些数据进行聚合并发送到汇聚节点，额外的负载将导致它们更快地耗尽能量而死亡。在某些无线传感器网络中，使用另一种称为网关的传感器节点作为网络中的簇头[13–15]。网关的能量由内部电池提供，其功率高于普通传感器节点的电池，但仍然是有限的。在采用网关作为簇头的无线传感器网络中进行聚类时，无需簇头选择阶段，因为网关是预先确定的簇头。

在聚类形成阶段，普通传感器节点被分配给网关。将一个传感器节点分配给网关会使该网关承担一定的负载。由于传感器节点的随机部署，一些网关因其附近传感器节点的密度较高而通常承受更大的负载。这种额外的负载会导致这些网关更早失效，从而缩短网络寿命并导致网络分割。因此，需要一种算法来解决将传感器节点分配给网关以形成簇的问题，使得网络中网关的最大负载最小化。该问题称为负载均衡聚类问题（LBCP），是一个NP‐hard问题[13]。在LBCP中，目标是将每个传感器节点恰好分配给一个网关。

聚类中每轮的最后阶段是数据传输。在此阶段，传感器节点将其感知数据发送给相应的簇头，然后簇头将其收集的数据发送到汇聚节点。

对于簇内连接性（即簇成员与其各自簇头之间的连接），通常采用单跳通信方法，因为传感器节点与其相应簇头之间的距离相对较短。然而，簇头与汇聚节点之间的距离相对较远。因此，对于簇间连接性（即簇头与汇聚节点之间的连接），多跳传输方法比单跳更节能，因为它消耗的功率更少。此外，在大多数无线传感器网络中，簇头不具备直接长距离与汇聚节点通信的能力。但在多跳无线传感器网络中，需要一种能量高效的路由算法来确定每个簇头的中继节点。

本文提出了一种面向无线传感器网络的能量均衡且高效的基于簇的路由协议。所考虑的无线传感器网络包含充当簇头的网关；因此，在提出的协议中，无需选择簇头。然而，为了在簇头之间平衡传感器节点的负载，并在网络中实现最优聚类，通过适当的近似算法求解LBCP。目前已知LBCP的最佳近似因子为1.5，并已证明不存在具有更优近似因子的多项式时间近似算法[13]。本文利用参数化复杂性理论设计一种近似算法，以获得更优近似因子来求解LBCP。设d_max为传感器节点的最大负载，n为输入实例的规模。我们提出了一种以参数化d_max为参数的固定参数可追踪近似（fpt‐approximation）算法，并具有1.1的近似因子。该fpt‐算法的时间复杂度为2^O(d_max log(d_max)) + O(n)，其指数级增长依赖于d_max而非输入规模。这使得该算法在大规模无线传感器网络中具有实用性，如第6节中的仿真所示。此外，提出了一种节能且能量均衡的路由算法，用于寻找连接网关到汇聚节点的最优路由树。本文的一些关键特点和贡献如下所述：

• 提出了一种针对LBCP的参数化max的1.1近似算法。
• 表明所提出的基于新近似 fpt算法的算法对于大规模无线传感器网络具有实用性。
• 提出一种路由算法，用于寻找簇头的数据消息传输到汇聚节点的路径。这些路径相对较短，并且网络内的所有节点均可访问。这些路径会在特定时间进行更换，从而使路由开销在所有节点之间分摊，进而实现节点间均衡的能量消耗。
• 通常，聚类与路由算法被结合到无线传感器网络的基于簇的路由协议中。该协议为LBCP提供了一个具有更好近似的解，并引入了一种针对无线传感器网络的更节能且能量均衡的路由算法。仿真结果表明，与一些以往类似的协议相比，所提出的协议提升了网络性能。

本文的其余部分组织如下。第2节回顾了关于无线传感器网络中聚类和路由协议的相关工作。第3节简要介绍了参数化复杂性的概念。第4节提出了系统模型和问题建模。第5节详细描述了新提出的聚类和路由算法。第6节对提出的协议与其他工作进行了详细的比较评估。最后，第7节总结了本研究并指出了若干未来的研究方向。

2. 相关工作

大量基于簇的路由协议已被提出用于无线传感器网络。其中一些协议考虑了LBCP，这意味着它们试图最小化簇头的最大负载。我们将它们分为两类。第一类包含考虑LBCP的协议，而第二类则包含不考虑LBCP的协议。

2.1. 考虑LBCP的协议

一种著名的LBCP近似算法已在[13]中提出，该算法的近似因子为1.5，时间复杂度为O(NN+ M+ q)，其中q是算法生成的二分图的边数。本文针对一种特殊情形的LBCP提出了一种精确算法，即所有传感器节点的流量负载相同的情况。该算法的时间复杂度为O(MN²)，其中M为网关数量，N为网络中的传感器节点数量。库伊拉和贾纳[16]将文献[13]中提出的近似算法的运行时间优化至O(NlogN)。这两种算法均在簇头之间平衡了传感器节点的负载。然而，在这些研究中，簇头直接将数据发送至汇聚节点。这种直接传输比使用中间节点的情况消耗更多能量。

LBCP已分别通过遗传算法（GA）和GA的改进版本在[17]和[18]中得到解决。在[17]中，遗传算法（GA）被用于求解LBCP以及无线传感器网络中的路由问题。在[18]中，传统遗传算法（GA）通过在初始种群生成和变异点选择阶段考虑传感器节点之间的连通性得到了改进。然而，[18]的一个缺点是其在簇头向汇聚节点传输数据时采用了直接传输方法，这会增加网络中的能量消耗。在[19]中，使用了差分进化（DE）的改进版本来求解LBCP。在此改进版差分进化中，相较于传统差分进化增加了一个额外的步骤，即局部优化阶段。然而，在该研究中，簇头采用直接传输方式将数据消息发送至汇聚节点，因此节点的能量消耗较高。

粒子群优化（PSO）是另一种用于解决LBCP[20, 15]的方法。在这些研究中，无线传感器网络中的聚类与路由问题通过PSO得以解决。在[20]中采用了适当的粒子编码方案，并在聚类和路由问题的适应度函数中考虑了重要参数。该算法节能，并相较于之前的研究提高了网络生命周期。然而，它并不具备能量均衡性。因此，在[15]中，作者在适应度函数中使用了其他参数，以提供一种节能且能量均衡的路由算法来解决聚类与路由问题。

2.2. 不考虑LBCP的协议

在[21, 22]中，无线传感器网络中的聚类与路由问题被表述为一个单一的多目标问题，即帕累托优化问题。这两种算法的主要区别在于，[21]采用多目标粒子群优化（MOPSO）方法来求解其帕累托优化问题，而[22]则使用超体积和Epsilon指标算法，这两种均为多目标进化算法。然而，两者均未在簇头之间平衡传感器节点的负载。

在[23]中，提出了一种用于无线传感器网络的平衡能量感知聚类与路由协议（BPA‐CRP）。BPA‐CRP将传感器区域划分为多个层，每层又进一步划分为若干个簇。每一层至少包含一个节点，称为转发器。簇头将其从簇成员接收到的数据发送给最近的转发器，而转发器负责将这些数据发送至汇聚节点。该协议的一个缺点是该网络在考虑LBCP时并未被划分为簇；实际上，是网络的初始划分导致了簇的形成。因此，传感器节点的负载在簇头之间并未得到均衡。此外，在该协议中，假设转发器可以在整个网络中广播消息，这在实际的无线传感器网络中是无法实现的。

在[24]中，聚类问题通过改进的布谷鸟搜索（CS）算法得到解决，而路由问题则通过改进的和声搜索算法解决。改进的布谷鸟搜索算法在普通传感器节点中找到最优的簇头集合。然后，改进的和声搜索算法找到一棵最优树以将簇头连接到汇聚节点。然而，该协议并未在簇头之间平衡传感器节点的负载。一种基于二型模糊逻辑（T2FL）的无线传感器网络的基于簇的路由协议已在[25]中提出。T2FL比一型模糊逻辑能更准确地处理不确定环境，因为T2FL的隶属度本身就是模糊集。该协议将节点划分为不同层次，并根据各层距离汇聚节点的距离为每层选择一个数值。然后，利用二型模糊逻辑进行聚类。之后，每个簇头根据其相邻簇头的层次数值向汇聚节点发送数据消息。然而，在该协议中，簇头的最大负载未被最小化，因此网络生命周期也未达到最大化。

聚类问题已在[26]中通过人工蜂群（ABC）解决。在该协议中，使用基于传感器节点能量水平和邻居信息的适应度函数来形成簇。本研究还提出了一种分布式路由算法，该算法在能量效率与路径跳数之间进行权衡。然而，该协议未考虑簇头的负载均衡。在[27]中，为无线传感器网络提出了一种基于簇的路由协议。在该协议中，所提出的聚类与路由算法在传感器部署后仅执行一次。聚类算法在汇聚节点上进行，且簇内通信为多跳方式。选择簇头的重要参数是节点的剩余能量，而路由算法中的重要参数是延迟以及节点与汇聚节点之间的距离。然而，该协议未考虑LBCP，因此传感器节点的负载在簇头之间未得到均衡。

在[40]，无线传感器网络（WSNs）中，聚类与路由问题已通过生物地理优化（BBO）方法得到解决。在该工作中，首先根据节点的剩余能量、簇头与其各自成员之间的平均距离以及簇头与汇聚节点之间距离的适应度函数，利用BBO选择簇头（CHs）。然后，通过另一个基于簇头剩余能量、每个簇头与汇聚节点之间的距离以及簇头节点度的适应度函数的BBO算法，计算每个簇头到汇聚节点的路由。然而，该方法并未最小化每个簇头的最大负载。

在[41]中，无线传感器网络中的聚类与路由问题通过粒子群优化（PSO）得以解决。该研究利用PSO来选择簇头（CHs），然后所提出的路由算法使用PSO寻找连接簇头到汇聚节点的最优路由树。该算法未考虑LBCP，且簇头之间的负载未实现均衡。在[42]中，无线传感器网络的聚类问题通过遗传算法（GA）得到解决。该研究采用一种改进版本的GA来选择簇头。所提出的启发式算法对传统遗传算法的交叉操作进行了修改，从而能够找到具有最优数量且分布合理的簇头的最佳配置。然而，该算法并未均衡簇头之间的负载，而是将每个传感器节点分配给其最近的簇头。该算法的另一个缺点是簇头与汇聚节点之间采用单跳通信方式。此外，另一种改进版本的遗传算法在[43]中被提出，该算法使用加权和法（WSA）将传感器节点分配给簇头。在[44]中，使用了一种元启发式算法——萤火虫算法来解决无线传感器网络（WSNs）中的聚类问题。该方法将节点与汇聚节点之间的距离视为一个重要参数，以降低网络中的延迟。

表1给出了所讨论协议的总结与比较。在该表对应“簇形成”的列中，“最近的簇头”表示为了形成簇，每个非簇头节点被分配给其最近的簇头。根据先前的研究，LBCP、聚类和路由问题均为NP难问题[13, 22]，已通过不同的近似方法加以解决。当我们在网络中考虑网关时，只需求解LBCP即可获得网络中的聚类结果。在求解LBCP时，诸如PSO之类的元启发式方法比诸如[13]之类的近似算法更为成功，因为LBCP的多项式难度为1.5。此外，元启发式方法无法对其输出提供近似因子。因此，设计一种具有近似因子的近似算法以对于此问题，期望获得优于1.5的近似因子。此外，还需要一种采用簇头与汇聚节点之间多跳通信方法的能量高效且能量均衡的路由算法。因此，本文提出了一种关于参数d_max的fpt‐近似算法，以1.1的近似因子求解LBCP，该近似因子优于此前为此问题提出的算法的近似因子。此外，我们引入了一种节能且能量均衡的路由算法，用于寻找连接网关到汇聚节点的最优路径。所提出的聚类与路由算法被结合成一种面向无线传感器网络的基于簇的路由协议。

3. 参数化复杂性

参数化复杂性是应对NP难问题这一核心问题的一种新方法。该领域由唐尼和费洛斯在[28, 29]中提出。参数化复杂性的核心概念是固定参数可追踪的（fpt）算法。考虑一个问题，设k是该问题实例的某个方面或部分，n是输入实例的大小。若关于参数k的算法的时间复杂度为f(k)×nc，其中f是仅依赖于k的任意函数，c为常数，则称该算法为fpt-算法。一个例子是顶点覆盖问题，这是一个NP完全问题。已经证明，对于规模为n的冲突图，顶点覆盖问题可以在少于1.29k+ kn步内求解。

[30]。该算法可实现于k ≤ 200，并且在计算生物学中有多种应用。

我们遵循[31]中的参数化复杂性的标准定义。设∑为一个有限字母表。一个判定问题由∑上的字符串集合Q⊆∑ 表示。一个问题的参数化是一个多项式时间可计算函数κ：∑ → N。参数化判定问题是(Q, κ)，其中Q⊆∑ 是任意一个判定问题，κ是一个参数化。换句话说，我们可以将一个参数化问题视为一个判定问题，其中每个输入实例x∈∑ 都关联一个正整数κ(x)。一个经典的判定问题可以根据其指定的参数产生无限多个不同的参数化判定问题。关于κ，若存在一个可计算函数f：N→N和一个多项式p，使得对于所有输入实例，该算法称为固定参数可追踪算法（fpt‐算法）。

every x ∈ ∑*, 该算法在输入x上的运行时间至多为f(κ(x))·p(|x|)。一个参数化问题(Q, κ)是固定参数可追踪的，如果存在一个关于κ的fpt‐算法来判定Q，则该问题是易处理的。有关参数化复杂性的更多细节，请参见[31, 32]。

参数化复杂性研究的是精确算法。然而，在本文中，我们利用参数化复杂性的概念来设计一种在fpt时间内运行的近似算法。实际上，这是一种能够生成具有近似因子的近最优解的fpt‐算法。这类算法被称为fpt‐近似算法。一个典型的例子是[33]中为带截止时间的度量TSP问题提出的算法，该问题不存在多项式时间的常数因子近似算法，除非P = NP。此外，它关于截止时间参数也不存在fpt‐算法。因此，单独使用近似算法或参数化复杂性均无法解决此问题。但在[33]中，已为此问题提出了一种时间复杂度为O(|n|³ + k!k)且具有2.5的近似因子的算法，其中n是输入实例的规模，k是截止时间顶点的数量。因此，将参数化复杂性与近似算法相结合，可以在参数值较小时得到高效的近似算法。

4. 系统模型与问题表述

4.1. 系统模型

考虑一个包含N个传感器节点、M个网关和一个汇聚节点的无线传感器网络。传感器节点和网关均匀且随机地分布在X×X的正方形区域内。所有节点和汇聚节点在部署后是静止的，并通过GPS获知自身位置。汇聚节点位于区域中心，具有无限资源。每个节点都知道汇聚节点的位置以及感知区域的大小（该信息可在节点部署前保存在其内存中）。只有当两个节点彼此处于对方的通信范围内时，才能建立通信。传感器节点只能被分配到其通信范围内的网关。数据收集操作被划分为若干轮次。在每一轮中，每个传感器节点感知本地数据并将其发送到各自的网关。然后，网关对数据进行聚合，并通过其他充当下一跳中继节点的节点将数据发送至汇聚节点。该能量模型与[8]中的模型相同。在此能量模型中，自由空间和多径衰落信道均取决于发射器与接收器节点之间的距离。无线电模块将k比特消息传输距离d所需的能量由公式计算。

(1).
E_Tx(k,d) = {
k·E_elec + k·ε_fs·d² if d < d₀
k·E_elec + k·ε_mp·d⁴ if d ≥ d₀
}

其中E_elec为电子电路所需能量，ε_fs和ε_mp为放大器所需能量，阈值d₀通过d₀ = √(ε_fs / ε_mp)计算得到。在此能量模型中，无线电模块接收k比特消息所需的能量由公式(2)计算。

E_Rx(k) = k·E_elec (2)

4.2. 问题表述

LBCP的正式定义如下。设S = {s₁, s₂, …, s_N}为传感器节点的集合，G = {g₁, g₂, …, g_M}为网关的集合，其中N和M ∈ N。在几乎所有的无线传感器网络应用中，我们有N > M。设d_i为传感器s_i的流量负载，其中s_i ∈ S，d_i ∈ N，且i ∈ {1, …, N}。设A_i为s_i可被分配到的网关集合，其中A_i ⊆ G。基于这些符号，该问题定义如下：

定义 1. LBCP
输入实例包含M, N, d₁, d₂, …, d_N ∈ N 和A₁, A₂, …, A_N，其中A_i ⊆ G且i ∈ {1, …, N}。该问题的一个解是集合S的一个划分S₁, …, S_M，其中S_i是分配给网关g_i的传感器集合，每个传感器s_j ∈ S被分配到A_j中的一个网关（j ∈ {1, …, N}）。目标是最小化max_{1≤i≤M} ∑_{j∈S_i} d_j。

本文为LBCP开发了一种fpt‐近似算法。为此，我们需要定义LBCP的决策版本，因为参数化复杂性涉及的是决策问题。设k为LBCP中需要优化的值的上界。LBCP的决策版本可定义如下。

定义 2. LBCP的决策版本
输入实例包含k, M, N, d₁, d₂, …, d_N ∈ N 和A₁, A₂, …, A_N，其中A_i ⊆ G且i ∈ {1, …, N}。目标是回答以下问题：是否存在一个成本至多为k的LBCP的解？

设d_max为传感器节点负载中的最大值（d_max = max_{1≤i≤N} d_i）。我们将d_max作为参数。此外，为了简化问题，我们将传感器节点的负载映射到区间[0, 1]内的有理数。为此，我们将d_i除以k，并将k映射为1。定义3给出了参数化d_max的LBCP的参数化版本，称为para‐LBCP。

定义 3. LBCP的参数化版本及参数d_max（para‐LBCP）
实例: M, N ∈ N, d₁, d₂, …, d_N ∈ Q 和A₁, A₂, …, A_N，其中A_i ⊆ G和i ∈ {1, …, N}
参数: d_max
目标: 是否存在成本至多为1的LBCP解？

5. 所提协议

本节描述了提出的节能且能量均衡的基于聚类的路由协议（EB‐CRP）。EB‐CRP将网络操作分为两个阶段：设置和稳态。这些阶段按顺序执行，直到网络生命周期结束。设置阶段本身包含三个子阶段：引导、聚类和路由。图2显示了提出的协议的各个阶段。

节点部署完成后，每个节点开始启动阶段。该阶段包括两个步骤。第一步是邻居发现，其中每个节点广播一条包含其标识和位置的信标消息。完成邻居发现后，每个节点将获知其邻接节点。在下一步中，每个节点的本地网络信息通过Hello消息传送到汇聚节点。EB‐CRP使用地理路由算法[1, 4]将这些Hello消息传送到汇聚节点。在地理路由中，每个节点的下一跳是距离目的地最近的邻接节点。每个接收到Hello消息的节点都以相同的方式进行转发。相比消耗大量节点能量的泛洪机制，地理路由算法要高效得多。

现在，汇聚节点运行聚类与路由算法，并利用其接收到的网络信息。其中聚类算法是一种用于求解LBCP的fpt‐近似算法，而路由算法则确定每个节点通往汇聚节点的下一跳中继节点。在聚类与路由算法完成后，汇聚节点通过受控泛洪机制广播其结果，该机制确保每个节点在已转发消息后不再重复转发。随后，每个网关创建一条时分多址（TDMA）消息并发送给其簇成员，通知它们可以传输数据消息的时间间隔。

TDMA可确保传感器节点通信时不会发生冲突。TDMA是一种广泛应用于无线传感器网络的多址接入方案。在TDMA中，每个簇头的可用信道带宽由所有簇成员共享，但簇成员按时间顺序轮流使用信道。换句话说，每个簇头的信道以循环方式通过无重叠的时隙依次分配给簇成员（即一个接一个）。簇成员仅可在其分配的时隙内传输消息，因此任何簇成员的传输都是非连续的。这种非连续传输还带来了较低的电池消耗，因为发射器在不使用时可以关闭，而这占据了大部分时间[37, 48]。因此，为了避免冲突，簇头需要向其簇成员发送TDMA消息。使用TDMA会导致延迟增加，因为传感器节点必须等待轮到自己才能向簇头发送消息。然而，使用TDMA提高了网络可靠性并减少了丢包。事实上，由于硬件限制，我们必须接受网络中的这种延迟[37, 45, 46]。

设置阶段结束后，所有节点进入稳态阶段，该阶段由75轮次[31]组成。在每一轮中，网关收集并聚合其簇成员发送的数据，并将这些数据传输至汇聚节点。接下来，我们将在以下两个小节中描述所提出的聚类与路由算法。

5.1. 基于fpt-近似算法的聚类算法

引导阶段结束后，聚类算法在汇聚节点内部执行。在此阶段，采用一种fpt‐近似算法将传感器节点分配给网关，以最小化网关的最大负载。

首先，我们描述一种用于求解para‐LBCP的fpt‐近似算法。然后，我们将该算法进行扩展，为LBCP提供一种fpt‐近似算法。设I是para‐LBCP的一个实例，opt(I)表示实例I的最优解中网关的最大负载。实例I存在解意味着可以将传感器节点分配给网关，使得每个网关的负载至多为1。因此，如果实例I存在解，我们称opt(I) = 1。以下定理为para‐LBCP提供了一种fpt‐近似算法。

定理1。 存在一个针对para‐LBCP的算法，该算法对每个长度为n的实例I，在2^O(d_max log(d_max)) + O(n)时间内计算出传感器节点到网关的分配，使得给定网络中每个网关的负载至多为1.1。

我们通过提出一个针对para‐LBCP的算法来证明定理1。该算法以para‐LBCP的一个实例I作为输入，并生成传感器节点到网关的分配方案，使得每个网关的负载至多为1.1，如果opt(I)= 1。根据传感器节点的负载，将它们划分为两个集合。设x为一个常数（稍后确定）。我们定义这些集合如下：

S_large = { d_i | 1 ≤ i ≤ N and d_i > M / (d_max + x) }
S_small = { d_i | 1 ≤ i ≤ N and d_i ≤ M / (d_max + x) }

该算法减少了S_large中不同负载的数量，并为其提供了上界。然后，通过动态规划将S_large中的传感器节点分配给网关。之后，采用贪心算法将S_small中的传感器节点分配给网关。fpt‐近似算法的伪代码在算法1中给出。接下来的两个小节描述了动态规划和贪心算法。

算法1 提出的用于求解fpt‐近似算法以解决para‐LBCP。
输入：M, N, d₁, d₂, …, d_N 和A₁, A₂, …, A_N
输出：传感器节点到网关的分配

1. S_large = { d_i | 1 ≤ i ≤ N and d_i > M / (d_max + x) }
   S_small = { d_i | 1 ≤ i ≤ N and d_i ≤ M / (d_max + x) }
2. 在S_large中找到不同负载数量的上界。
3. 通过动态规划将S_large中的传感器节点分配给网关。
4. 通过贪心算法将S_small中的传感器节点分配给网关。
   End

在算法1中，根据负载将传感器节点划分为两个集合：S_large和S_small。然后，通过动态规划将S_large中的传感器节点分配给网关。最后，贪心算法将S_small中的传感器节点分配给网关。

5.1.1. 动态规划

At first, by the linear and geometric grouping techniques [34, 35], 可得到S_large中不同负载数量的上界。然后，动态规划在考虑该上界的条件下将S_large中的传感器节点分配给网关。在描述这些分组技术如何用于求解para‐LBCP之前，先简要介绍这些方法。

设I为para‐LBCP的一个实例，Σ(I)表示传感器节点的负载总和，m(I)表示不同负载的数量，a(I)表示实例I中的最小负载。若对于每个传感器x ∈ I，均存在一个从I到J的一一映射函数f(x)，使得d_x ≤ d_f(x)，则在实例I和J上定义了一个偏序≤，记作I ≤ J。显然，如果I ≤ J，则opt(I) ≤ opt(J)且Σ(I) ≤ Σ(J)。

线性分组将传感器节点划分为组G₁、G₂、…、G_q。设k为一个正整数。在线性分组技术中，传感器节点根据其负载按降序排列。前k个传感器节点（负载最大的k个传感器节点）被放入G₁，接下来的k个传感器节点（接下来负载次大的k个传感器节点）被放入G₂，依此类推。因此，我们有G₁ ≥ G₂ ≥ … ≥ G_q且除最后一组外的所有组满足|G_i| = k。

现在，每个组G_i中每个传感器节点的负载增加到其组的最大负载。这个新组表示为G’ i。现在我们有G’₁ ≥ G₁ ≥ G’₂ ≥ G₂ ≥ … ≥ G’_q ≥ G_q和∪ {i=2}^q G’ i ≤ I ≤ ∪ {i=1}^q G’_i。G’_i中的负载称为四舍五入的负载。

设J = ∪_{i=2}^q G’_i 且 J’ = G’_1。现在，我们有以下引理。

引理 1.([34]) ：在使用参数k进行线性分组后，我们有
- opt(J) ≤ opt(I) ≤ opt(J) + k
- Σ(J) ≤ Σ(I) ≤ Σ(J) + k

几何分组是线性分组的细化。设I为para‐LBCP的一个实例。对于r = 0, 1, …, log₂(1/a(I))，令I_r表示负载位于区间(2⁻⁽ʳ⁺¹⁾, 2⁻ʳ)内的传感器节点构成的实例。将参数k’ = k应用于I_r进行线性分组，得到实例J_r和J’_r。令J = ∪_r J_r 且 J’ = ∪_r J’_r。现在，我们有以下引理。

引理 2.([34]) ：在使用参数k进行几何分组后，我们有
- opt(J) ≤ opt(I) ≤ opt(J) + k·log₂(1/a(I))
- Σ(J) ≤ Σ(I) ≤ Σ(J) + k·log₂(1/a(I))
- m(J) ≤ 2k·Σ(I) + log₂(1/a(I))

引理1和引理2的证明见[34]。我们对S_large应用几何分组。设α = log₂(d_max + x/M)。对于r = 0, 1, …, α，令I_r表示负载位于(2⁻⁽ʳ⁺¹⁾, 2⁻ʳ]内的那些传感器节点构成的实例。由于区间(2⁻⁽ʳ⁺¹⁾, 2⁻ʳ]覆盖了每个传感器节点d在(M/(d_max + x), 1]中的所有负载，因此存在一个r，其中r ∈ {0, 1, …, α}且d ∈ I_r。于是，S_large中的传感器节点被划分为实例I₀, I₁, I₂, …, I_{α−1}和I_α。接下来，在每个I_r上应用线性分组。设M·log₂(d_max)·d_max / 2^r为在实例I_r上应用线性分组的参数。对每个实例I_r，通过应用线性分组得到集合G_{r,i}。然后，通过增加G_{r,i}中每个传感器节点的负载，得到集合G’ {r,i}。现在，令J_r = ∪ {i≥2} G’ {r,i} 且 J’_r = G’ {r,1}。为I_r生成的每个组（可能最小的组除外）的基数等于M·log₂(d_max)·d_max / 2^r。令J = ∪ {r=0}^α J_r 且 J’ = ∪ {r=0}^α J’_r。图3显示了在应用几何分组之前和之后的S_large。

引理 3. 在J ∪ J’中不同负载的数量等于O(d_max / log₂(d_max))。

证明。设n(I_r)为I_r中传感器节点的数量。我们有
Σ(I_r) ≥ (1/2^{r+1})·n(I_r) ≥ (1/M·log₂(d_max))·(d_max / 2^r)。

在I_r中的最小分组可能少于M·log₂(d_max)·(d_max / 2^r)个传感器节点。这意味着
m(J_r) − 1 ≤ (2·Σ(I_r)) / (M·log₂(d_max)·d_max)。

我们知道当x ≥ x时，对所有x ≥ 0成立，因此我们有
m(J_r) ≤ (2·Σ(I_r) × d_max) / (M·log₂(d_max)) + 1。

传感器节点在J中的总负载数量按如下方式计算：
∑ {r=0}^{log₂(d_max+x/M)} m(J_r) ≤ ∑ {r=0}^{log₂(d_max+x/M)} [(2·Σ(I_r) × d_max)/(M·log₂(d_max)) + 1]
≤ (2·d_max)/(M·log₂(d_max)) · ∑_{r=0}^{log₂(d_max+x/M)} Σ(I_r) + log₂(d_max+x/M) + 1。

由于所有传感器节点均被分配到M个网关，因此
Σ(S_large) = ∑_{r=0}^{log₂(d_max+x/M)} Σ(I_r) ≤ M。

因此，我们有
∑_{r=0}
S_large中的负载。(b)将S_large划分为实例Io、I1, I2,…、Iα−1和Iα。(c)为示例Ir创建组。(d)对实例Ir中的负载进行取整。)

log₂(d_max+x/M) m(J_r) ≤ (2·d_max)/(M·log₂(d_max)) × M + log₂(d_max+x/M) + 1
= (2·d_max)/log₂(d_max) + log₂(d_max+x/M) + 1。

根据引理4，我们有d_max + x ≥ M。因此，我们有
∑_{r=0}^{log₂(d_max+x/M)} m(J_r) ≤ (2·d_max)/log₂(d_max) + log₂(d_max+x/M) + 1
= O(d_max / log₂(d_max))

因此，J中不同负载的数量等于O(d_max / log₂(d_max))。另一方面，J’中有log₂(d_max + x/M) + 1个组，每组有一个不同的负载。因此，J’中不同负载的数量等于O(log(d_max))。因此，在J ∪ J’, 中位于(M/(d_max + x), 1]内的不同四舍五入的负载数量为B = O(d_max / log₂(d_max)) ∪ O(log(d_max)) = O(d_max / log₂(d_max))。

设x₁, x₂, …, x_B为不同的四舍五入的负载。动态规划将向量(q₁, q₂, .... q_B)定义为网关g的一种模式，其中q_i (1 ≤ i ≤ B)表示被分配给网关g且四舍五入的负载等于x_i的传感器节点数量。对于每个x_i，有q_i·x_i ≤ M。已知x_i > M/(d_max + x)，因此可得q_i ≤ M/x_i ≤ M·(d_max + x)/M ≤ d_max + x。当且仅当∑_i q_i·x_i ≤ 1，并且对于每个x_i ∈ {x₁, …, x_B}，存在至少q_i个具有等于x_i的四舍五入负载的传感器节点时，模式p = (q₁, q₂, .... q_B)对网关是可行的到该网关通信范围内的x_i。对于每个网关，最多有(d_max + x + 1)^O(d_max / log₂(d_max)) = 2^O(d_max log(d_max))种可行模式。

动态规划的第一轮迭代针对网关g₁，下一轮针对g₂，接着是g₃，依此类推，直到最后一轮针对g_M。对于网关g_i（其中i = 1, 2, …, M），它计算一个由向量（a₁,…, a_B）组成的集合V_i，每个向量中的a_j表示分配给网关g₁,…, g_i的负载为x_j的传感器节点数量。每个集合V_i的基数最多为(d_max + x + 1)^O(d_max / log₂(d_max)) = 2^O(d_max log(d_max))。为了计算下一个集合V_{i+1}（从一个网关转移到另一个网关），每个网关g_{i+1}的可行模式将被添加到集合V_i的每个元素中。该动态规划包含M次迭代，每次迭代可在2^O(d_max log(d_max)) × 2^O(d_max log(d_max))时间内实现；因此，动态规划的时间复杂度为2^O(d_max log(d_max)) × 2^O(d_max log(d_max)) × M，等于2^O(d_max log(d_max))。

如果opt(I) = 1，则集合V_M至少包含一个向量(b₁, b₂, …, b_B) ∈ V_M，其中b_i是J ∪ J’中具有四舍五入负载x_i的传感器节点数量，且b₁ + b₂ + … + b_B是最优解中使用的J ∪ J’, 中的传感器节点数量。

现在我们描述如何计算将传感器节点集J ∪ 和J’中的节点分配给网关的方法。我们运行动态规划算法以计算所有集合V_c，其中c = 1, …, M。然后，我们定义一个M‐一致M‐部超图（简称为M‐图）G = (V₁, V₂, …, V_M, E)，其中
E = {(z₁, z₂, …, z_M) | z_i ∈ V_i 且 z_i中的传感器节点+ 1 − z_i可分配给网关g_{i+1}}。

两个向量z_i = (a₁, …, a_B) ∈ V_c 和 z_{i+1} = (a’₁, …, a’ B) ∈ V {i+1} 在M‐图中相连，当且仅当z_{i+1} − z_i中的传感器节点可以被分配给网关g_{i+1}。这意味着z_{i+1} − z_i是网关g_{i+1}的一个可行模式。因此，如果输入实例I存在一个解，我们就可以确定存在一个至少有一条边的端点为(b₁, b₂, …, b_B) ∈ V_M。以(b₁, b₂, …, b_B) ∈ V_M为端点的边表示将J ∪ J’中的传感器节点分配给网关的一个可行分配。上述M‐图可在2^O(d_max log(d_max))时间内计算得出。图4展示了问题实例I的一个M‐图示例。在此示例中，我们假设opt(I) = 1。

在将传感器节点分配给网关后，四舍五入的负载被替换为其原始值。然后，下一节中给出的贪心算法将S_small中的传感器节点分配给网关。过程1中的第1到17行展示了将J ∪ J’中的传感器节点分配给网关的步骤。

5.1.2. 贪心算法

在本节中，我们描述了贪心算法，该算法将S_small中的传感器节点分配给网关。当算法执行到此步骤时，我们知道S_large中的传感器节点已经被分配给了g₁、g₂、…、g_M。贪心算法认为，除一个网关最多可承担1.1的负载外，其余每个网关最多可承担1的负载。贪心算法的正确性由引理4提供证明。

贪心算法按顺序将传感器节点分配给网关。对于每个传感器节点，算法首先检查其是否可以分配给网关g₁。要将一个传感器节点分配给某个网关，必须满足两个条件：第一，它们之间必须在彼此的通信范围内；第二，分配后该网关的流量负载不得超过1。如果该传感器节点无法分配给g₁，算法将尝试将其分配给g₂。此过程持续进行，直到该传感器节点被分配到一个网关为止。如果该节点仍无法被分配到任何网关，则算法会再尝试一次分配，但在这一轮中，每个网关的容量将增加至1.1。过程1中的第18到33行展示了贪心算法的具体步骤。该贪心算法的时间复杂度等于O(NM)。

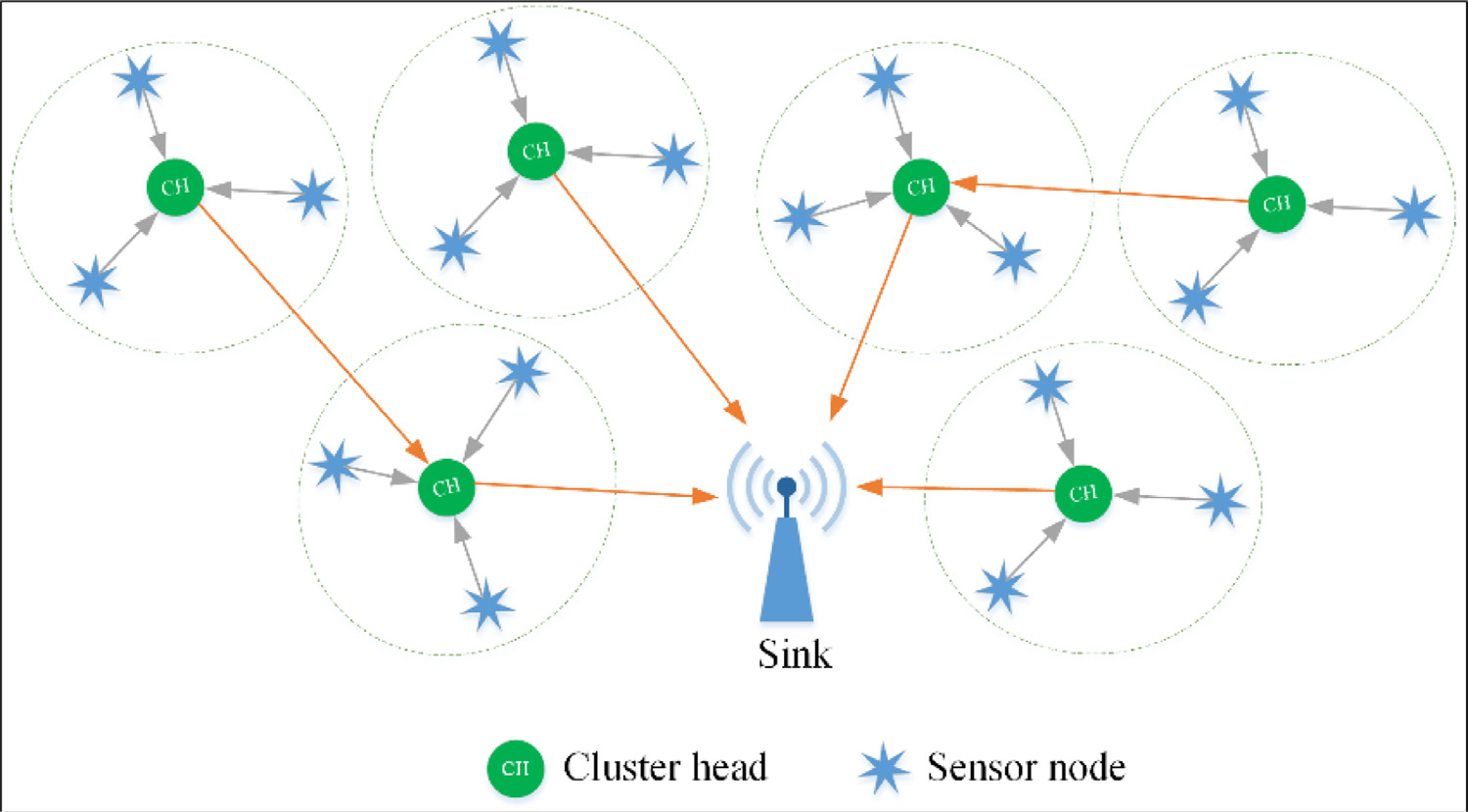
Procedure 1 动态规划与贪心算法。

1. / 将S_large和S_small中的传感器节点分配给网关 /
2. 对于每个g_i
3. 对于g的每个可行模式p_i
4. 对于V的每个成员v_{i−1}
5. V_i = V_i ∪ (p + v);
6. 结束循环
7. 结束循环
8. 结束循环
9. 对于c = 1到M−1
10. 对于每个z ∈ V_c 且 z′ ∈ V_{c+1}
11. 如果((z′ − z)可以被分配给g_{c+1})那么
12. 在图中连接z和z′；
13. 结束如果
14. 结束循环
15. 结束循环
16. Output1 = 图中边对应的分配；
17. 将Output1中的四舍五入的负载替换为其原始值；
18. 对于S_small中的每个传感器节点s_i
19. 标志 = false;
20. 对每个网关g
21. 如果（Output1.负载[g] + d_i) ≤ 1 且 g ∈ A_i），则
22. 将s_i分配给g；
23. 标志 = true;
24. 结束如果
25. 结束循环
26. 如果（标志 == false），则
27. 对于每个网关g
28. 如果（（Output1.负载[g] + d_i) ≤ 1.1 且 g ∈ A_i）那么
29. 将s_i分配给g；
30. 结束如果
31. 结束循环
32. 结束如果
33. 结束循环
    End

引理4。 如果opt(I) = 1 且x = 10 × (100,000)² + 1000 + 1，则该算法在将一个网关的容量视为1.1而其余网关的容量视为1的情况下，将所有传感器节点分配给网关。

证明。本引理通过反证法进行证明。假设S_small中的传感器节点需要的容量高于M + 0.1，因此分配给网关的传感器节点的总负载高于(M + 0.1)(1 − M·d_max + x) ≥ M + 0.1 − M²·d_max + x。如果x > M·d_max，则M·d_max + x > M·d_max。因此，传感器节点的总负载高于M，导致opt(I) > 1，这产生了矛盾。为了使算法正确运行，x必须是一个大于M的常数。因此，不失一般性，我们对M定义一个上界，然后基于该上界确定x。我们考虑M ≤ 10,000；即，该算法对于少于10,000个网关的网络能够正确运行。已知d_max。如果x ≥ 10 × (100,000)² + 1000 + 1，则引理得证，且fpt‐近似算法成立。该算法能够正常工作于无线传感器网络，其网关数量最多为10,000。在具有N个传感器节点的无线传感器网络中，文献[8]表明，簇头的最佳数量为0.05 × N。因此，上述关于M的上界几乎等同于无穷大。然而，如果无线传感器网络中的网关数量超过10,000，则只需将M的上界增加到算法正常工作所需的值即可。

算法1可按如下方式开发以解决LBCP问题。通过二分查找确定问题判定版本中定义的k的最小值。然后，将传感器节点的负载和k都除以k。最后，算法1将传感器节点分配给网关。因此，我们得到以下定理。

定理2。 存在一种用于LBCP的算法，该算法将传感器节点分配给网关，对于长度为n的实例I，其时间复杂度为2^O(d_max log(d_max)) + O(n)，使得给定网络中每个网关的负载至多为1.1 × opt(I)。

如第6节所示，该算法适用于大规模无线传感器网络。当传感器节点被分配给网关后，下一节中给出的路由算法将运行，以连接簇头与汇聚节点。

5.2. 簇间多跳路由算法

聚类算法完成其操作后，路由算法将在汇聚节点内部执行，该算法为每个节点确定通往汇聚节点的下一跳中继节点。在采用多跳通信方法的无线传感器网络中，靠近汇聚节点的节点除了发送自身的数据消息外，还必须转发从距离汇聚节点较远的节点接收到的数据消息。因此，靠近汇聚节点的节点电池会迅速耗尽，这一问题被称为热点问题。热点的出现会导致网络分割。此外，即使少数靠近汇聚节点的节点死亡，来自更远节点的数据消息也必须经过更长的路径才能到达汇聚节点，从而降低了网络的能量效率。因此，路由算法除了需要节能外，还必须平衡靠近汇聚节点的节点的能量消耗，以延长网络生命周期。

为了实现节能且能量均衡的路由算法，我们选择若干条称为主路径的路径，数据消息将通过这些主路径发送到汇聚节点。这些路径在算法每次运行时都会以适当的方式进行更换。换句话说，该算法在每次运行时确定不同的节点子集来构成主路径。汇聚节点通过考虑一个与传感器区域具有相同中心的虚拟方形结构来确定主路径。位于这些虚拟方格上的节点

虚拟方格的对角线上的节点，或至少是离这些对角线最近的节点，构成主路径。共有四条主路径，每条为主对角线的一半。图5展示了虚拟方形结构，该结构将区域划分为两个不同的部分：一部分在正方形外部，另一部分在正方形内部。

该正方形的目标是控制数据发送到汇聚节点的路径，使得靠近汇聚节点的节点能量消耗保持均衡。设R为网关的通信范围。如果正方形的边长为网关通信范围的四倍（4R），则汇聚节点的邻接节点（在其一跳或两跳通信距离内）将落入该正方形中。这些节点更可能提前死亡，从而导致热点问题。因此，我们选择正方形的边长等于4R。汇聚节点知晓区域的长度、节点的位置以及网关的通信范围。因此，它可以计算每条对角线的两个端点，并确定每个节点相对于虚拟基础设施的位置。汇聚节点持有一个内部变量α，如图5所示。该变量的初始值为45，表示水平轴与主路径3之间的夹角。α的应用将在下文描述。

虚拟方格外的节点使用地理路由算法将其数据消息发送到汇聚节点。它们将消息向汇聚节点转发，直到被位于方格内部或方格边上的某个节点接收为止。位于方格内部或方格边上的节点不仅转发自身的消息，还转发从外部节点接收到的消息，将其传向主路径上的节点。主路径由最靠近方格对角线的节点组成。总而言之，内部节点将所有数据消息转发至主路径，而主路径上的节点则将消息转发至汇聚节点。图6展示了网络中数据消息的流向。

5.2.1. 正方形内路由

在本节中，我们讨论方格内节点的路由方式。汇聚节点根据主路径为方格内的每个节点选择下一跳中继节点。首先，我们描述路径的构建过程。起初，汇聚节点计算虚拟方格四个角的坐标。对于坐标为(x, y)的角点，汇聚节点计算位于(x, y)半径R范围内的每个节点的一个称为优值的值，如公式(3)所示。

merit = a × (E/E₀) + b × (1/dist) (3)

其中a和b是两个常数，E表示节点的剩余能量，E₀表示每个网关的初始能量。在选择路径的第一个节点时，dist表示该节点与坐标(x, y)之间的距离。如果在(x, y)的半径R范围内没有节点，则汇聚节点将计算在(x, y)的半径2R范围内的每个节点的优值。这一过程将持续进行（所考虑的区域范围会逐步扩大），直到至少找到一个节点为止。汇聚节点选择具有最大优值的节点作为该路径的第一个节点。设s₁为选中的节点。从这一步开始，在路径构建过程中，dist表示节点与汇聚节点之间的距离。此时，汇聚节点计算s₁的所有邻接节点的优值，然后选择优值最大的节点作为该路径的第二个节点。此过程持续进行，直到某个汇聚节点的邻接节点被选中为止。

公式(2)中的参数a和b分别等于0.2和0.8。这些值是通过仿真确定的，意味着提出的协议在这些a和b取值下具有更好的网络性能。其原因是，节点到对角线的距离在路径形成中必须比其他参数更具影响力。这样，路径将更靠近对角线生成，而对角线正是路径最初预期所在的位置（参见图5）。

现在，路径已经形成，汇聚节点确定正方形内每个节点的下一跳中继节点。设s_r为一个节点

算法2 方格内部路由。
输入：节点信息
输出：方格内的节点的主路径和下一跳

/ 主路径的构建 /
1. 将正方形内每个节点的下一跳设置为未定义。
for each 主路径
3. 找到路径的起点（坐标（x，y））。
4. 考虑一个以（x，y）为中心、半径为R的圆。
5. 如果圆内没有节点，将半径增加到2R, 3R,…直到在圆内至少找到一个节点。
6. 选择圆内优值最大的节点作为路径的第一个节点。
7. while（所选节点不是汇聚节点的邻居）
8. 将前一个节点中具有最大优值的邻居节点选为路径的下一个节点。
9. 结束当
10. 结束 for
11. / 正方形内每个节点的下一跳 /
12. for each 正方形内下一跳未定义的节点
13. 找到到该节点的最近路径。
14. 计算该节点每个邻居的优值。
15. 选择优值最大的节点作为该节点的下一跳。
16. 结束 for
End

其下一跳尚未确定。汇聚节点找到距离s_r最近的主路径，然后计算s_r每个邻接节点的优值，其中dist是该节点到s_r最近路径的距离。随后，汇聚节点选择优值最大的节点作为s_r的下一跳。算法2展示了方格内部路由的不同步骤。

为了平衡汇聚节点附近节点的能量消耗，路由算法通过旋转虚拟正方形来改变主要路径。该过程将在下一节中详细说明。

5.2.2. 主路径的变更

The routing algorithm is 每75轮 执行一次。在算法的每次执行中，虚拟方格将沿逆时针方向旋转，以改变主路径的位置。为此，在每次执行路由算法后，汇聚节点将α 增加30°，当汇聚节点计算虚拟方格角点的位置时，会考虑角度α。30是α的一个合适的增量值，该值通过仿真确定。图7显示了算法四次运行中方格的旋转情况。

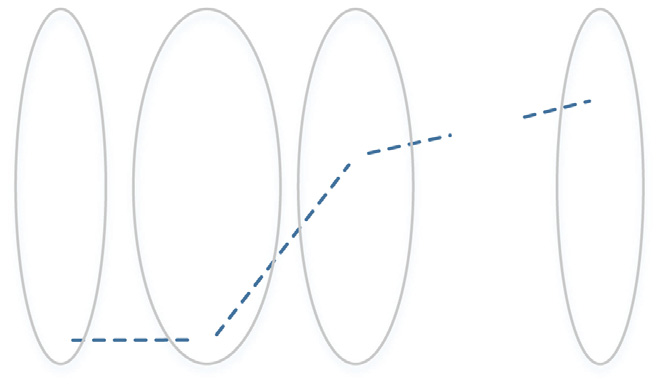、(b)、(c)和(d)分别显示了算法的前四次执行结果。)

6. 性能评估

我们通过仿真评估了提出协议的性能和实用性。EB‐CRP及其他所有提及的协议均在OMNeT++中实现，OMNeT++是一个模块化、基于组件的C++仿真库和框架，主要用于构建网络仿真器。MiXiM框架是一个OMNeT++建模框架，可用于仿真无线传感器网络。我们使用该框架对无线传感器网络进行更真实的仿真。数论库（NTL）[36]是一个用于处理向量和矩阵的高性能C++库。因此，我们使用NTL实现提出的fpt‐近似算法。仿真在搭载2.4 GHz CPU和8 GB内存的Intel Core i7处理器上运行，操作系统为Microsoft Windows 10平台。

为了进行仿真，我们考虑了两种不同的网络场景（NET1和NET2）。在这两种场景中，传感器节点的总数在300到900之间变化，网关数量在40到80之间变化。NET1和NET2中的传感器区域大小分别为350 m × 350 m和750 m × 750 m。每个传感器节点的初始能量为2.0焦耳，每个网关为10.0焦耳。本文仿真的结果是基于35次平均得出的运行。仿真参数及其取值假设与[8]相似，并在表2中给出。

表2 仿真参数。
| 参数 | 值 |
| :— | :— |
| 传感器节点数量 | 300–900 |
| 网关数量 | 40–80 |
| NET1中的区域 | 350 × 350m |
| NET2中的区域 | 750 × 750m |
| 仿真迭代次数 | 35 |
| 每个传感器节点的流量负载 | 10 B/ms–64 B/ms |
| 数据包大小 | 40 字节 |
| 控制包大小 | 200 位 |
| 传感器节点的通信范围 | 70 m |
| 网关的通信范围 | 120 米 |
| 传感器节点的初始能量 | 2.0 焦耳 |
| 网关的初始能量 | 10.0 焦耳 |
| E_elec | 50 nJ / 比特 |
| ε_fs | 10 皮焦 / 比特² |
| ε_mp | 0.0013 pJ / (bit m⁴) |

传感器节点有多种不同的射频收发器模块[37]。例如，Chipcon CC2420是一种射频收发器，其最大数据速率为32 B/ms（字节/毫秒），其完整数据表可在[38]中找到。新型号射频收发器的最大数据速率等于64 B/ms[39]。为了更接近实际情况，我们从10–64 B/ms范围内随机选择每个传感器节点产生的流量负载。

为了评估EB‐CRP协议的性能，将其仿真结果与提出的协议[22]（称为Pareto）、基于PSO的协议[15]、BPA‐CRP[23]以及1.5‐近似算法[13]（称为1.5‐app）进行了比较。通过将EB‐CRP协议与Pareto和基于PSO的协议进行比较，展示了在解决无线传感器网络中的聚类与路由问题时，使用所提出的fpt‐近似算法和路由算法与使用粒子群优化等元启发式方法和多目标方法之间的差异。将EB‐CRP协议与BPA‐CRP进行比较，展示了使用所提出协议与基于虚拟层基础设施的协议之间的差异。通过将EB‐CRP与1.5‐app进行比较，展示了使用所提出的fpt‐近似算法与1.5‐近似算法之间的差异，以及使用多跳通信方法与单跳通信方法之间的差异。针对所有算法进行的仿真实验具有

图8. NET1中网络生命周期的比较：(a) 40个网关和(b) 80个网关。

图9. 比较 在NET2中关于网络生命周期的（a）40个网关 (b) 80个网关

same<参数>值，如表 2中所给。现在，我们评估各协议的网络性能。

6.1. 网络性能评估

在本节中，从网络生命周期、汇聚点吞吐量、能量消耗、死亡节点数量和延迟等方面对EB‐CRP的网络性能进行了评估。首先，我们比较了各协议的网络生命周期，网络生命周期定义为直到75%的节点死亡时所经历的轮数。这一定义是合理的，因为只要仍有足够数量的节点存活，网络就能继续运行。我们在NET1和NET2上分别将传感器节点数量从300到900变化，并设置40和80个网关的情况下运行了这些算法。结果如图8（NET1）和图9（NET2）所示。

通常，增大区域大小会缩短网络生命周期，因为消息源与目的地之间的距离增加了。在无线传感器网络中，网络生命周期有多种定义。在[7]中给出了这些定义的一些示例。本研究基于所使用的网络生命周期的定义

本文中，随着网络中节点数量的增加，网络生命周期将减少。这是因为更多的节点通常会产生更多的数据包。更多的数据包会导致节点负载增加，尤其是靠近汇聚节点的节点。尽管增加节点数量会提高网络中的总能量，但也会导致节点（特别是靠近汇聚节点的节点）转发更多数据包，从而使其能量消耗更快，即它们会更早死亡。由于本文所定义的网络生命周期与网络中存活节点的数量直接相关，因此增加节点数量将降低网络生命周期。此外，在使用单跳通信方式的算法（如1.5‐app算法）中增加节点数量也会降低网络生命周期。其原因是距离较远的节点数量会增加，而根据本文的能量模型，发送数据包的能量消耗与其源和目的地之间的距离成正比，因此这些远距离节点的能量消耗更高。当网络中传感器节点数量增加时，距离汇聚节点较远的节点数量也随之增加。这些远距离节点

图10. 700个传感器节点在（a）NET1和（b）NET2中汇聚点吞吐量的比较。

其他节点消耗更多能量，因此会更早死亡。较远节点的提前死亡导致网络生命周期缩短。与其它协议相比，EB‐CRP具有更长的网络生命周期。这是因为：第一，它采用更精确的算法求解LBCP，从而更好地在簇头之间均衡传感器节点的负载；第二，在每次路由算法运行时，它生成不同的路径将数据消息从簇头发送到汇聚节点，从而更好地在网络节点间分摊路由开销。帕累托协议的网络生命周期比PSO、BPA‐CRP和1.5‐app更长，因为在定义的帕累托优化问题中使用了更合适的参数，并且通过超体积指标和_epsilon指标算法进行求解，能够在网络中实现更优的聚类与路由。BPA‐CRP协议未能在簇头之间均衡传感器节点的负载。此外，转发节点采用单跳通信方式将数据消息发送至汇聚节点，这种方式能耗极高。因此，BPA‐CRP具有比EB‐CRP、Pareto和PSO的网络生命周期更短。1.5‐app算法网络生命周期在这些协议中是最短的，因为它在簇头和汇聚节点之间采用单跳通信方式。

接下来，我们从汇聚点吞吐量的角度对算法进行比较。我们将吞吐量定义为在仿真时间内汇聚节点成功接收到的数据包数量。图10显示了在NET1和NET2上，网关数量从40变化到80、传感器节点数量为700个时，各算法在汇聚点吞吐量方面的比较结果。在BPA‐CRP中，汇聚点的吞吐量高于其他协议，因为它具有更长的网络生命周期。

现在，我们从总能耗的角度比较这些算法，总能耗定义为网络中节点通信（包括发送和接收消息）所消耗的总能量。第r轮消耗的总能量

图11. 在（a）NET1和（b）NET2中，针对800个传感器节点和50个网关的能量消耗比较。

是根据公式(4)计算的。
Eng_Consumed(r) = Eng_Initial − Eng_Remain(r) (4)

其中，初始能量是节点的总初始能量，根据公式(5)计算得出；剩余能量 (第r轮)是第r轮时节点的总剩余能量，根据公式(6)计算得出。
Eng_Initial = ∑ {i=1}^N Esn₀(i) + ∑ {i=1}^M Eg₀(i) (5)
Eng_Remain(r) = ∑ {i=1}^N Esnᵣ(i) + ∑ {i=1}^M Egᵣ(i) (6)

其中，N和M分别为传感器节点和网关的数量，Esn₀(i)表示传感器节点s_i的初始能量，Eg₀(i)表示网关g_i的初始能量，Esnᵣ(i)表示第r轮传感器节点s_i的剩余能量，Egᵣ(i)表示第r轮网关g_i的剩余能量。我们在NET1和NET2中对800个传感器节点和50个网关运行了算法，以测量总能耗。结果如图11所示。

图11显示，与其他协议相比，EB‐CRP的每轮能耗更低。然而，EB‐CRP在降低每轮能耗的同时延长了网络生命周期，这意味着它通过在每一轮中消耗更少的能量来实现更长时间的运行。其原因是构成路径的节点不断变化，每组节点仅在网络生命周期的短时间期间内形成这些路径。此外，这些路径的变化方式使得大多数节点在网络生命周期的某个时刻都会参与其中。因此，该算法实现了能量消耗的均衡。此外，该算法是节能的，因为它为发送数据消息选择短路径。BPA‐CRP和1.5‐app在网络中采用单跳通信方式，因此在所提及的协议中具有最高的能量消耗。Pareto的能量消耗略低于PSO，因为Pareto在其帕累托优化问题中使用了更合适的参数，并通过最优求解该优化问题实现了更好的网络路由。

接下来，我们从死亡节点数量随轮数的变化角度对算法进行比较。我们在700个传感器节点和60个网关的条件下运行各算法，以测量NET1和NET2中的死亡节点数量。因此，网络中共有760个节点。结果如图12所示。可以看出，我们所提算法优于其他所有提及的算法。这是因为我们更好地在簇头之间均衡了传感器节点的负载，使得簇头更晚死亡，同时所提出的路由算法具有能量高效和能量均衡的特性，能够更好地在网络节点之间分配路由开销，从而避免热点产生和节点过早死亡。

最后，我们在NET1和NET2中将传感器节点数量从300到900变化，并设置70个网关，运行算法以比较平均延迟。结果如图13所示。延迟定义为源节点发送数据包时刻与汇聚节点接收到该数据包时刻之间的平均时间。该指标根据公式(7)计算得出。
Delay = (∑_{i=1}^{n_packets} (Tr_i − Ts_i)) / n_packets (7)

其中，n_packets是所有源‐汇聚节点对的数据包数量，Tr_i表示汇聚节点接收第i个数据包的时刻，而Ts_i表示源发送第i个数据包的时刻。

根据公式(7)中给出的延迟定义，本指标未考虑所提出的fpt‐近似算法的运行时间。该fpt‐近似算法的运行时间将在下一节中进行计算。延迟表示数据包的新鲜度。为了在本实验中对算法进行公平比较，我们未考虑算法1.5‐app和BPA‐CRP，因为1.5‐app采用簇头与汇聚节点之间的单跳通信，而BPA‐CRP采用转发节点与汇聚节点之间的单跳通信。单跳通信在现实中无法实现。

通常，随着传感器节点数量的增加，流量也会增加，因此网络中的延迟也将增加。此外，当传感器区域的尺寸变大时，节点到汇聚节点的距离增加的概率也更高。因此，在较大的区域内，节点必须通过更多的跳数将其消息发送到汇聚节点。更多的跳数会增加网络中的延迟。因此，较大的传感器区域在网络中具有更高的延迟。图13显示，PSO和帕累托算法的延迟高于EB‐CRP。这是因为在PSO和帕累托算法中，靠近汇聚节点的节点更早死亡，因此远离汇聚节点的节点必须通过更长的路径以更多跳数将消息发送到汇聚节点。然而，EB‐CRP避免了靠近汇聚节点的节点过早死亡以及热点问题。因此，节点可以在更长时间内以最少的跳数通过最短路径传输其消息。

下一节评估了fpt‐近似算法的运行时间，并讨论了其在大规模无线传感器网络中的实用性。

6.2. 运行时间评估

在本节中，我们证明了所提出的fpt近似算法对于大规模无线传感器网络是实用的。尽管该算法的时间复杂度是指数级的，但它仅在d_max上呈指数级增长，这使得其运行速度明显快于在N或M上呈指数级的情况，例如针对LBCP的穷举搜索，该方法需要检查所有可能的分配方案，数量等于M^N = O(2^N log M)，以找到一个解。在本实验中，我们考虑d_max的两个取值：32和64，因为在实际无线传感器网络中d_max的最大值为64 B/ms，如前一节所述。表3展示了所提出算法与LBCP穷举搜索之间的比较。本文认为，若某算法求解问题实例的运行时间超过三小时，则该算法不具实用性。对于N = 20且M = 10或更大的问题实例，穷举搜索是不实用的。然而，fpt‐近似算法对于包含超过6000个传感器节点和100个网关的问题实例仍然是实用的，因为fpt‐近似算法中选择的参数与网络规模无关；这意味着随着网络规模的增大，参数的大小不会增加。

图13. 在(a) NET1和(b) NET2中，针对70个网关的平均延迟比较。

表3 运行时间评估（分钟）。
| N | M | d_max | fpt-近似算法 | 穷举搜索 |
| :— | :— | :— | :— | :— |
| 20 | 10 | 32 | 0.2 | >180 |
| 20 | 10 | 64 | 0.3 | >180 |
| 50 | 20 | 32 | 0.5 | >180 |
| 50 | 20 | 64 | 0.7 | >180 |
| 100 | 30 | 32 | 1.1 | >180 |
| 100 | 30 | 64 | 1.5 | >180 |
| 200 | 50 | 32 | 2.8 | >180 |
| 200 | 50 | 64 | 3.9 | >180 |
| 500 | 80 | 32 | 8.2 | >180 |
| 500 | 80 | 64 | 11.5 | >180 |
| 1000 | 100 | 32 | 19.8 | >180 |
| 1000 | 100 | 64 | 27.6 | >180 |
| 2000 | 100 | 32 | 48.3 | >180 |
| 2000 | 100 | 64 | 67.5 | >180 |
| 4000 | 100 | 32 | 118.7 | >180 |
| 4000 | 100 | 64 | 166.2 | >180 |
| 6000 | 100 | 32 | 175.4 | >180 |
| 6000 | 100 | 64 | 245.6 | >180 |

7. 结论和未来工作

本文中，我们提出了一种基于簇的无线传感器网络路由协议。该提出的协议通过具有1.1的近似因子和运行时间为2^O(d_max log(d_max)) + O(n)的fpt‐近似算法来解决LBCP问题。该运行时间仅在d_max上呈指数级增长，因此适用于大规模无线传感器网络。此外，还提出了一种能量感知路由算法，用于将簇头连接到汇聚节点。通过以更精确的近似因子求解LBCP，并在每个簇头与汇聚节点之间提供更高效的路由，从而实现了更好的网络性能。与许多其他类似协议进行了比较。作为该研究方向的未来工作，我们提出两个问题：第一个是改进所提出的fpt‐近似算法的运行时间；第二个问题是针对本文提到的参数，设计一个求