第5章 优化无线传感器网络中的簇头选择以延长其存在时间
5.1 引言
目前,无线传感器网络(WSNs)被广泛应用于许多环境中,例如智慧城市应用,用于监控与跟踪。通常,所有传感器都由一次性电池供电,这使得节能成为一个迫切需求 [1–8]。因此,传感器管理是延长无线传感器网络可用性的重要因素 [9]。需要一个优化过程 [10, 11, 13, 14]来优化传感器性能,同时不影响效率。
有各种类型的传感器,它们在所提供的功能上略有不同[15]。传感器节点可以采用机械、生物、化学或磁传感器,以满足工业、军事应用、精准农业应用和医疗监控应用的需求,同时具有较低的实施和维护成本。传感器节点具备双重能力:首先,它们能够感知多种环境条件,如压力、声级、温度、湿度变化、振动等;其次,它们还具备计算能力。为了实现节点间通信,采用多跳通信方式。这有助于将感知数据从源节点快速传输到相应目的地或特定主节点。网络拓扑和节点分布取决于应用性质[16–21]。维持其运行较为困难
由于传感器依靠电池供电,传感器节点长时间运行时操作受限。此外,为传感器节点充电或更换电池也非常困难。当传感器节点在恶劣环境中使用时,存在许多限制,如电池电量有限且难以充电、存储能力有限、互操作性问题等。传感器节点的低功耗和低处理能力要求通过制定合理的调度方法避免不必要的感知活动,以实现能量守恒。无线传感器网络面临的另一个最大挑战是路由协议的优化设计,原因在于存在多种网络约束,如节点随机部署、能量消耗、数据传输模型、节点能力、网络动态以及数据聚合等。
为了提高网络可用性和可扩展性,已设计出多种网络拓扑结构。其中一种是聚类模型,即将传感器分组成簇。该模型能够改善网络在其寿命方面的性能[22]。在聚类无线传感器网络中,每个簇通常至少包含一个代理节点,通常称为簇头(CH)。簇头可由网络设计者动态确定或预先指定。簇与基站之间的通信由该簇头来实现。正确选择簇头将直接影响网络寿命。在无线传感器网络中,网络寿命通常是最重要的问题。除了通过改进传感技术来降低数据采集的能量消耗外,更理想的情况是无线传感器网络中的传感器节点具有相等的寿命,从而使整个网络达到最大的可用性。为了平衡单个节点和整个网络的可用性,选择合适的簇头成为关键步骤。已有许多方法被提出以满足这一需求[23–28]。
近年来,关于无线传感器网络(WSN)能效的研究在文献中大量出现 [24, 26, 29],,并提出了多种协议和算法,以实现在基于簇的无线传感器网络中最佳的功率节约[23, 27]。但大多数研究未能在动态环境中提供较长的系统寿命,其中传感器处于无人看管状态,且其电池很难充电。低能耗自适应聚类分层(Low‐Energy Adaptive Clustering Hierarchy, LEACH)是最具前景的基于簇的路由协议之一[30]。LEACH 是一种分布式单跳聚类算法。假设所有节点都能够执行长距离传输至基站(BS)。因此,簇头(CH)的选择取决于所有簇所使用的能量。HEED 是另一种基于节点剩余能量和邻居节点的基于簇的算法[31]。
之前大多数方法的问题在于假设在所有轮次中簇的数量保持固定。这一假设无法保证获得能够最大化网络寿命的合适簇头数量。此外,在许多应用中,我们无法提前确定簇的数量。而且,在动态无线传感器网络环境中,传感器节点可能会不时改变其位置,此时固定的网络结构假设是低效的。因此,我们提出一种新方案,用于在动态环境中构建网络结构,并利用遗传算法 [32–36] 选择簇头。在我们提出的方法中,网络结构可能在每轮之后根据不同情况而有所不同。
节点的特性。这些特性将决定网络中的簇头以及簇的数量。这些特性包括:
- F1:平均距离。
- F2:脆弱性指数。
- F3:剩余电池电量。
- F4:邻居数量。
- F5:预期消耗能量。
此外,我们的模型还使用了一组假设,例如:所有节点都受到能量限制。所有簇都是同构的,但它们的大小可能不同。同构簇意味着所有节点具有相同的特性。只有一个基站。
第5.2节描述了所提出的模型,以展示其如何形成网络簇。此外,第5.3节描述了所提出的算法及其参数。最后,在第5.4节中,我们讨论了结果及相应的验证。
5.2 无线传感器网络构建
5.2.1 相关工作
给定感知区域中的传感器节点根据与其他节点的最近距离被划分为不同的簇。此处采用基于簇的方法进行路由,并将当前能量最大的节点选为簇头,其余节点作为簇成员。因此,在每个簇中,剩余能量最大的节点被选举为簇头(CH)。
存在许多旨在最大化网络寿命 [37] 的算法。这里我们假设网络是安全的,且无需额外的安全措施 [38–42]。MODLEACHST [43] 是一种基于 LEACH 的新方法,可提供最长的网络寿命。但其结果受限于有限数量的传输。M‐GEAR [44] 根据传感器节点在感知区域中的位置将其划分为四个逻辑区域。M‐GEAR 在每个独立区域内选择簇头(CHs)。然而,在该方法中,簇头是通过概率方式选择的。此外,稳定选举协议(SEP)是一种为每个可能成为簇头的节点赋予加权概率的协议 [45]。在 DEEC [46], 中,每个节点的现有能量遵循一定的准则来决定其是否成为簇头。阈值敏感稳定选举协议(TSEP) [47] 是另一种方法,但它是为异构网络设计的。改进的分布式能量高效聚类(DDEEC) [48] 能够根据节点的残余能量,在所有网络节点中均衡地进行簇头选择。
智能算法在无线传感器网络等复杂动态环境中提供了表现出智能行为的自适应机制[49]。各种研究[49–53]讨论了基于簇的无线传感器网络中依赖于智能算法的路由协议。在GA‐WCA中,负载均衡因子被视为权重之一,同时考虑所有邻居节点到簇头的距离之和。LA2D‐GA仅将距离作为计算适应度函数的参数;然而,染色体的表示形式是一个二维网格,这反映了无线传感器网络的有效统计信息[54]。
在大多数使用遗传算法(GA)管理无线传感器网络(WSN)的研究中,主要目标是在预先确定簇数量的前提下选择簇头(CH)。此外,簇头选择过程仅依赖于每个节点的四个因素,如参考文献[50, 51, 53, 55]所述。这些因素包括节点到簇中心的距离、剩余电池电量、移动程度和脆弱性指数。而在其他一些近期研究中,例如[52],,仅考虑了两个参数用于簇头选择(邻居数量和残余能量)。但我们认为,仅依靠这些因素不足以利用遗传算法有效完成簇头选择过程。在本研究中,我们通过引入两个额外的参数来延长网络生命周期。这两个新增参数为:(i) 节点的消耗能量;(ii) 邻居节点的数量。
第一个参数可反映该节点未来能够传输和接收的数据量,而第二个参数被引入的原因在于数据的接收与发送所消耗的能量与数据量大小相关。此外,簇头需负责基站(BS)与其所属簇内所有节点之间的全部数据转发。引入这两个因素的目的在于延长网络寿命,因为选择最合适的簇头将直接影响网络的整体性能。同时,我们将采用遗传算法(GA)来获取网络的最佳结构。这种方法在动态环境中尤为有效,特别是在簇的数量不固定的情况下。
遗传算法(GA)是一种模拟某些自然过程的自适应搜索方法:选择、信息、遗传、随机突变和种群动态[56]。GA从一组字符串组成的种群开始,然后生成后续的字符串种群。一个简单的GA包含三个算子[50]:交叉、复制和变异。GA的染色体以适合遗传算子和适应度函数的形式,包含了给定问题解决方案的所有基本构件。
在我们的问题中,每个提议的网络结构都被表示为一条染色体。该结构根据传感器节点的特征提出。我们的工作基于以下假设:选择节点作为簇头的主要因素包括该节点与其所有邻居之间的平均距离、节点的脆弱性指数、移动程度、剩余电池电量、邻居数量以及消耗的能量。此外,每个因素的优先级程度不同。因此,我们根据网络设计所对应的应用场景为每个因素分配特定的权重。最后,利用遗传算法结合这些因素构建网络结构,将产生最佳的簇头数量,并提高网络寿命。
5.2.2 路由协议和簇头选择
自组织路由协议可分为两大类:基于拓扑和基于位置。基于拓扑的路由协议利用网络中存在的链路信息进行分组转发。基于位置的路由协议则利用节点的地理位置来做出路由决策,从而可能提高效率和性能。基于拓扑的路由可进一步分为两种方法:主动式和反应式方法。在自组织网络中,主动式路由协议会周期性地广播控制消息,以使每个节点始终知道到达所有目的地的当前路由。但即使这些路径当前未被使用,它也会维护有关可用路径的路由信息。一些主动式路由协议包括目的序列距离向量(DSDV)、源树自适应路由(STAR)和无线路由协议(WRP)。而反应式路由协议仅维护当前正在使用的路由,从而减轻网络负担,适用于无线环境,因为它们在需要路由数据包时才启动路由发现过程。这类协议包括动态源路由(DSR)协议、按需距离向量路由(AODV)协议、Ad−hoc Ondemand Multi−path 距离向量(AOMDV)协议以及时序有序路由算法(TORA)协议。
从相关研究工作来看,一个必须考虑的重要方面是实现诸如数据准确性、最小化延迟和最小化能耗等QoS参数,以提高传感器节点寿命。优化[57–59]是在给定约束条件下,根据选定的优化目标函数,获得决策变量最佳取值的过程。为了拓宽优化方法在不同问题领域的适用性,通常利用物理和自然原理来开发鲁棒的优化算法。模拟退火(SA)、进化算法(EA)、粒子群优化(PSO)和蚁群优化(ACO)就是这类算法的几个例子。多路径路由的效率取决于路径的构建及其物理分布。路径选择决定了多路径路由的性能。如果所选路径彼此独立或具有协作性,则多路径路由可提升性能。因此,提出了节点不相交路径路由协议以避免路径间的干扰。多路径路由协议可通过将冗余信息经由备用路径传送到目的地来提供容错性。使用节点不相交路径,可以同时实现容错性和负载均衡。在自组织网络中寻找节点不相交路径是一项具有挑战性的任务,这是因为自组织网络环境中的协议应具备局部化和分布式特性。如果已知网络拓扑结构,则存在标准方法可用于发现给定节点对之间的节点不相交路径。协议可能识别也可能无法识别给定节点对之间的所有节点不相交路径。
给定传感器节点的坐标,两个节点之间的距离可以用欧氏距离(ED)来近似。也就是说,距离因子可以通过计算节点与其所有邻居之间的距离之和,以及该节点与基站之间的距离来得到。例如,具有邻居数量为 K 的节点 v 的距离因子 D 可表示如下
$$
D_v = \sum_{j=1}^{k} ED_{v,j} + ED_{v,BS} \quad (5.1)
$$
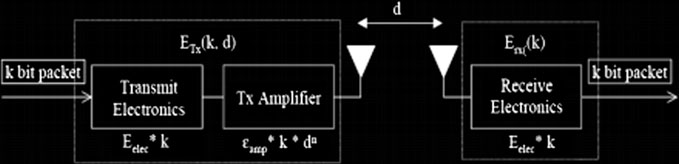
消耗的能量E表示将聚合消息从簇传输到基站所需的能量。根据图5.1所示的一阶无线电模型,发送一个长度为k比特、距离为d的消息所消耗的能量可通过以下公式计算。
对于包含k个成员节点的簇,簇传输能量定义为[60, 61]。
$$
E = \sum_{j=1}^{k} ET_{jh} + kER + ET_{hs} \quad (5.2)
$$
公式5.2的第一部分表示从k个成员节点向簇头发送消息所消耗的能量。第二部分表示簇头从成员节点接收k条消息所消耗的能量。最后,第三部分表示簇头向基站传输消息所需的能量。从节点i向节点j传输长度为l比特的消息所消耗的能量($ET_{ij}$),以及接收该l比特消息所消耗的能量(ER)分别由以下公式给出:
$$
ET_{ij} = lE_e + l\varepsilon_l d^4_{ij}, \quad (5.3)
$$
$$
ET_{ij} = lE_e + l\varepsilon_s d^2_{ij}, \quad (5.4)
$$
and
$$
ER = lE_e + lEBF, \quad (5.5)
$$
其中$d_{ij}$表示节点之间的距离。然而,对于长距离传输(例如从簇头到基站的传输),所消耗的能量与$d^4$成正比。EBF 表示采用波束成形方法降低能量消耗的能耗成本。此外,节点 v 的剩余电池电量(用RP(v) 表示)可通过以下表达式计算
$$
ERP(v) = E_s - \sum_{t=0}^{c} (ET_v(t) + ER_v(t)), \quad (5.6)
$$
其中$E_s$为节点的初始能量,c为当前时间。节点v的邻居数量(记为N(v))是指距离d小于或等于 β的节点总数(β根据无线传感器网络的覆盖范围因应用而异)
$$
N(v) = |n_i| \Leftrightarrow dvni \leq \beta : (v \neq n_i \& \beta > 0) \quad (5.7)
$$
最后,基于 [62],一个具有高脆弱性指数的节点意味着该节点的失效可能导致整个网络断开。因此,应避免该节点成为簇头。节点 v的脆弱性指数 VI可根据公式5.8计算。
$$
VI_v = \frac{N_v^{before}}{N_v^{after}} \times \frac{L_v^{before} + 1}{L_v^{after} + 1}, \quad (5.8)
$$
其中,$N_v^{before}$表示移除v节点前的节点数量,$N_v^{after}$表示移除v节点后的节点数量,$L_v^{before}$表示移除v节点前的层级数,$L_v^{after}$表示移除v节点后的层级数。
5.3 提出的遗传算法聚类方法
每个网络结构由一组比特表示。结构中的比特数等于网络节点的数量。每个节点根据其在网络结构中的角色用0或1表示。值为1的比特代表簇头,值为0的比特代表普通传感器节点。因此,1的个数即为簇的数量。图5.2展示了具有15个节点和5个簇的网络染色体示例。
生成一组随机网络结构后,遗传算法将使用公式f chromosome计算每种5.9的适应度。请记住,此处的目标是最大化f chromosome
$$
f_{chromosome} = \left[\sum_{i=1}^{|CH|} f_{ch_i}\right] + \frac{1}{|CH| + |N_{CH}|}, \quad (5.9)
$$
其中N为节点数量, $|CH|$ 为所提出网络结构中的簇的数量,NCH为具有以下两个特性的节点:首先,它被选为簇头(在簇内没有其他节点与其相连);其次,它与最近的簇头之间的距离小于或等于 β。
每个簇的$f_{ch}$函数值都会被计算。该值取决于我们提出的用于选择簇头的五个特征。假设每个特征i具有特定的权重$w_i$,该权重根据应用需求表示其优先级。$f_{ch}$可如公式5.10所示表达
$$
f_{ch} = \frac{1 + \sum_{i=3,4} W_i F_i}{1 + \sum_{i=1,2,5} W_i F_i}. \quad (5.10)
$$
除了适应度函数外,我们还应根据公式 5.11计算每个染色体的选中概率 $p(s_i)$。该值 $p(s_i)$ 将决定染色体$i$ 在交叉或变异过程中被选中的机会。其正式表达式如下所示
$$
p(s_i) = \frac{f(i)}{\sum_{x=1}^{n} f(x)}, \quad (5.11)
$$
其中n是种群中染色体的数量。遗传算法开始于复制阶段,我们使用加权轮盘赌选择下一代的交配池。
该算法通过根据网络信息(如节点数量、特征权重和遗传算法参数)生成大小为N的初始染色体种群来工作。每条染色体包含随机数量的簇头。对于每条染色体,我们通过计算所有节点的特征并将每个节点分配到一个簇中来计算其适应度。然后,算法计算每条染色体的适应度函数,并使用轮盘赌法计算实际选择该染色体的次数。接着,根据各自的比率执行变异、交叉和复制过程。这些过程将重复进行,直到满足终止条件。之后,将根据适应度值选择最佳的网络结构。
5.4 簇头用于多跳聚类模型
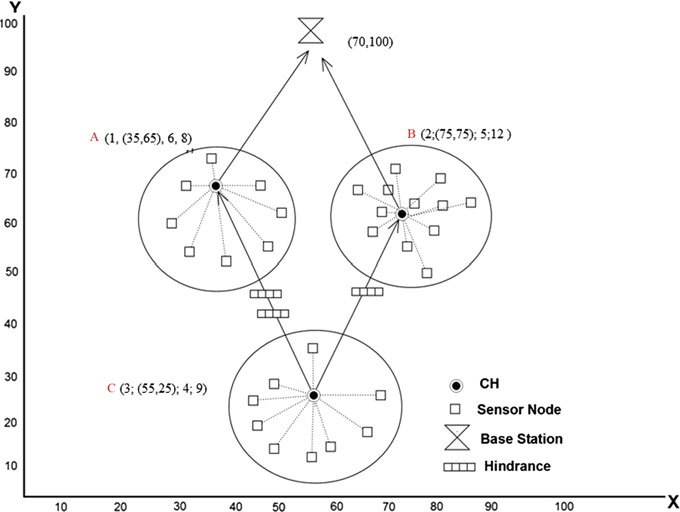
多跳聚类模型是一种聚类模型的特殊情况,其中由于某些原因(例如距离过长),簇头无法直接将数据传输到基站。在这种情况下,簇头会尝试寻找另一个更靠近基站的簇头,作为它们之间的网关。现在假设我们有一个无线传感器网络,该网络包含一组由上述簇头选择模型形成的簇。每个簇在固定轮次的数据传输中具有特定的簇头。每轮结束后,基站根据所有节点的可用信息(如剩余能量、位置和邻居)为每个簇选择一个新的簇头。同时假设,如果某些簇头与基站之间的距离超过 α,则它们无法直接向基站传输数据。这些簇头必须将其数据传送到其与基站之间的中间簇头。因此,我们在创建簇并确定每个簇的簇头后,提出了一种简单的算法来构建多跳模型。所提出的算法基于A‐Star(A∗)算法[]。该算法的目标是通过选择能量消耗最小的路径来延长网络寿命。我们假设该算法将在每轮所有簇头向基站发送数据后,在基站上运行,以重构网络层次结构。基站将对距离其超过阈值 α的簇头运行该算法。该算法通过结合g(n)(到达簇头的成本)和h(n)(从簇头到达基站的成本)来评估簇头n。算法选择f(n)最小的簇头。设我们需要确定从其到基站最佳路径的初始簇头为i,簇头n的剩余能量为En,i与n之间障碍物的数量为 |Hi, n|,则成本函数可按公式(5.12)、(5.13)和(5.14)计算。
$$
f(n) = g(n) + h(n) \quad (5.12)
$$
$$
g(n) = ED_{i,n} + E_n + |H_{i,n}| \quad (5.13)
$$
$$
h(n) = ED_{n,BS} + |SN_n| \quad (5.14)
$$
其中 |SN_n| 表示簇中 n上的节点数量。将簇的节点数量纳入计算以表示簇头的流量负载。ED是能量感知距离,表示两个节点之间的期望距离。ED可根据图5.3计算。经过多次迭代后,该算法从簇头x到基站选择路径 [x, BS],该路径为最小能耗路径。该协议假设每个簇头均可到达其环境中的任何其他簇头,如算法3所示,其中N为簇头的数量。

算法3: 多跳聚类算法
[1t]: 初始化 α;
2: 对于 x = 0, 1, ..., CHs do
3: 如果 ED_{x,基站} ≤ α then
4: [x,基站] = Φ,其中 Φ 表示 x 与基站之间的直接链路
5: else
6: 对于 i = 0, 2, ..., N do
7: h(i) = ED_{i,基站} + \|传感器节点_i\|
8: g(i) = ED_{i,x} + E_i + \|H_{i,x}\|
9: f(i) = g(i) + h(i)
10: 结束循环
11: [x,基站] = Min(f.items),即簇头与所有其他簇头之间的最小距离
12: 结束如果
13: 结束循环
14: 返回多跳结构;
从表格5.1可知,节点C将选择簇头B作为其父节点,因为该簇头具有最小的成本值。
给定传感器节点的坐标,可以通过考虑它们的剩余能量来近似计算两者之间的能量感知距离ED。ED的值通过结合节点间的欧氏距离和环境障碍进行计算。节点与其簇内所有其他节点之间的障碍物(如树木或建筑物)也被纳入考虑。为了计算节点V与节点B之间的ED,假设B与V之间的欧氏距离为DVB。同时假设使用欧氏距离来计算V与其簇头之间的距离DVC。V与簇内任何其他节点之间的每个障碍物为H,簇内障碍物总数为nh。簇中的节点数量为n。每个障碍物具有一个权重W,表示其消耗节点能量的能力。设W= {w1; w2; w3; …wnh},其中每个H的ID由wi的索引i表示。因此,ED可表示为公式(5.15)
$$
ED_V = D_{VC} + \sum_{i=1}^{n} \sum_{j=1, i \neq j}^{n} \sum_{ik=0}^{nh} [H_{ij} * w_i] + D_{VB} \quad (5.15)
$$
在计算簇头 i 与基站之间的距离时,ED 可通过简单的欧几里得距离($ED_{i,BS} = D_{i,BS}$)进行计算。算法4展示了所提出的 ED 算法的主要步骤。
算法4:能量感知距离算法
1: 获取以下项的位置坐标:B , V, C,
2:设置 e = 0;
3: 计算 D_{VB} = √((x_B − x_V)^2 + (y_B − y_V)^2)
4: 计算 D_{VC} = √((x_C − x_V)^2 + (y_C − y_V)^2)
5: for i = 1, 2, ..., N do
6: 对于 j = 1, 2, ..., 节点数量执行
7: 对于 k = 1, 2, ..., nh do
8: e = e + W[k] * H_{ij}
9: 结束循环
10: 结束循环
11: 结束循环
12: ED = (e + ED_{V,基站} + ED_{V,C})
13: 返回 ED
5.5 实验结果与讨论
所提出的算法已使用MS Visual C# 2010开发环境进行编程和测试。首先,执行了两次仿真配置,每种配置运行8次,以测试我们方法的网络寿命和吞吐量,并与一些传统方法和最新方法进行比较。每种配置代表了如前所述的不同环境特征。最后,进行了第三次仿真,将我们方法与无线传感器网络中的一些基于遗传算法的算法进行了对比。结果表明,与现有协议相比,网络寿命和吞吐量得到了最大化。第一次仿真的网络参数如表5.1所示,输出结果见表5.2和图 5.4。
表5.2 第一次仿真的网络参数
| 网络参数 | 值 |
|---|---|
| 传感器数量 | 100 |
| 基站位置 | (50, 50) |
| 网络区域 | 100 m² |
| 每个传感器的初始能量 | 1.0 焦耳 |
| 空闲状态能耗 | 50 纳焦耳/比特 |
| 数据聚合能耗 | 5 纳焦耳/比特/报告 |
| 放大能量 (d ≥ d₀) | 10 pJ/比特/米² |
| 放大能量 (d < d₀) | 0.0013 pJ/比特/米² (E_fs/10 = E_fs₁) |
| 放大能量 (d ≥ d₁) | — |
| 放大能量 (d < d₁) | Emp/10 = Emp₁ |
| 数据包大小 | 400 比特 |
第二次仿真的网络参数如表格5.3所示,其性能结果如表格5.4和图 5.5 所示。第三次仿真的网络参数与第一次仿真相同。我们在第三次仿真中使用了以下遗传算法参数:种群大小= 20,代数 = 30,交叉率= 0.8,变异率 = 0.006,以及轮数 = 1000。第三次仿真的结果如表格5.5所示。
使用首次仿真参数,结果表明网络吞吐量有显著提升,如表格5.6和图 5.6(表 5.7)所示。
表5.3 第一次仿真的结果
| 算法 | 首次死亡 | 50% | 最后死亡 |
|---|---|---|---|
| LEACH | 523 | 1084 | 1402 |
| HEED | 603 | 1100 | 1510 |
| SEP | 674 | 940 | 2003 |
| PEGASIS | 1251 | 1693 | 2611 |
| M‐GEAR | 512 | 932 | 1989 |
| MODLEACH | 668 | 1101 | 2517 |
| TSEP | 711 | 1004 | 2271 |
| DDEEC | 1495 | 1801 | 3169 |
| 我们的方法 | 1591 | 2037 | 3424 |
表5.4 第二次仿真的网络参数
| 网络参数 | 值 |
|---|---|
| 传感器数量 | 400 |
| 基站位置 | (450, 450) |
| 网络区域 | 400 m² |
| 每个传感器的初始能量 | 1.0 焦耳 |
| 空闲状态能耗 | 50 纳焦耳/比特 |
| 数据聚合能耗 | 5 纳焦耳/比特/报告 |
| 放大能量 (d ≥ d₀) | 10 pJ/比特/米² |
| 放大能量 (d < d₀) | 0.0013 pJ/比特/米² (E_fs/10 = E_fs₁) |
| 放大能量 (d ≥ d₁) | — |
| 放大能量 (d < d₁) | Emp/10 = Emp₁ |
| 数据包大小 | 400 比特 |
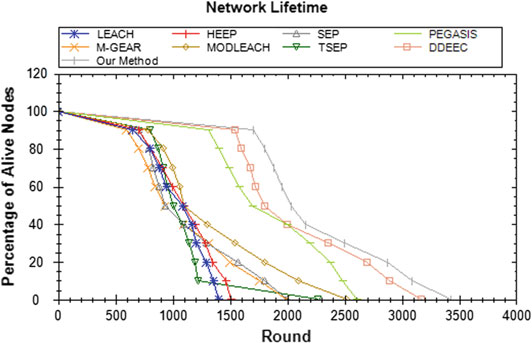
表5.5 第二次仿真的结果
| 算法 | 首次死亡 | 50% | 最后死亡 |
|---|---|---|---|
| LEACH | 1232 | 1570 | 2300 |
| HEED | 1345 | 1804 | 2643 |
| SEP | 1571 | 2189 | 3210 |
| PEGASIS | 2065 | 3100 | 4356 |
| M‐GEAR | 1090 | 1700 | 2900 |
| MODLEACH | 1800 | 3290 | 3913 |
| TSEP | 2100 | 3120 | 3800 |
| DDEEC | 2460 | 3273 | 4120 |
| 我们的方法 | 2601 | 3586 | 4712 |
表5.6 第三次仿真的结果,显示第一次节点死亡(FND)的轮次以及每轮时间(秒)
| 算法 | FND | 50% | 每轮时间 | 总时间(分:秒) |
|---|---|---|---|---|
| HCR | 933 | 1104 | 2 | 29:51 |
| 我们的方法 | 1591 | 2037 | 1.5 | 24:32 |
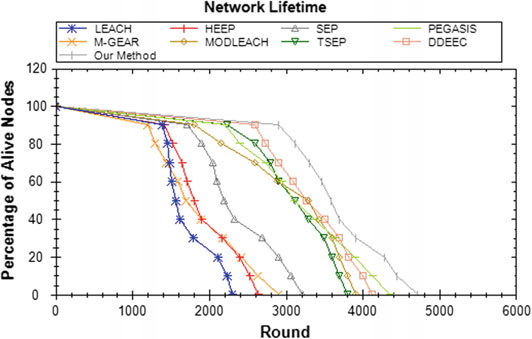
Table 5.7 网络吞吐量结果
| 算法 | 轮次 (500) | 轮次 (1500) | 轮次 (2000) |
|---|---|---|---|
| LEACH | 2.9×10⁴ | 3.2×10⁴ | 3.2×10⁴ |
| TSEP | 2.1×10⁴ | 2.8×10⁴ | 3×10⁴ |
| MODLEACH | 4×10⁴ | 5.5×10⁴ | 5.6×10⁴ |
| DDEEC | 5×10⁴ | 5.8×10⁴ | 6.1×10⁴ |
| 我们的方法 | 5.5×10⁴ | 6.1×10⁴ | 7.6×10⁴ |
5.6 结论
提出了一种构建无线传感器网络结构以优化其吞吐量的新方法。为了减少能量消耗,所提出的算法将在每轮结束后根据网络中各节点的当前状态在基站处运行。该算法已通过不同环境特征与其他现有算法进行了测试。结果表明,与其它现有方法相比,本文提出的方法能够延长网络寿命并提高吞吐量。




















 56
56

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








