基于狼群算法的WSN覆盖优化

一种面向覆盖的无线传感器网络拓扑结构优化新策略

王树欣1,游海荣2,岳 Yinggao1,3和曹丽 1

摘要

针对复杂工业应用环境中无线传感器网络的关键优化问题，如最佳覆盖和网络可靠性，提出了一种基于狼群算法的面向覆盖的无线传感器网络拓扑优化策略。结合无线传感器网络拓扑结构的特点以及狼群算法的优化思想，重新定义了狼群的游走和突袭行为。提出一种新的头狼变异策略，扩大了最优解的邻域搜索范围，增强了狼群分布的均匀性和狼群搜索的遍历能力，显著提高了狼群算法的计算速度和精度。周期性地以相同概率随机选择簇头，将无线传感器网络的总体能耗均匀分配到各传感器节点，实现簇内成员节点数据的均衡分布，完成无线传感器网络拓扑优化的设计。通过算法仿真与结果分析表明，与粒子群优化算法和人工鱼群算法相比，狼群算法在传感器节点的残余能量、平均传输延迟、平均分组投递率以及网络覆盖等方面均表现出优势。其中，与粒子群优化算法和人工鱼群算法相比，节点的剩余能量分别提高了9.5%和15.5%，网络的平均覆盖率分别提高了10.5%和5.6%。

关键词 物联网，无线传感器网络，拓扑结构，狼群算法，覆盖优化

收稿日期：2020年10月29日；接受日期：2021年1月15日
责任编辑：陈燕娇

引言

在自然科学与技术快速发展的背景下，物联网技术和无线传感器网络（WSNs）被广泛应用于军事、智能制造、工业监控、智慧农业、环境监测、智能物流和交通等领域。无线传感器网络是融合了无线通信技术、计算机处理技术和传感器技术等多种现代技术的网络系统。无线传感器网络主要由微型传感器节点组成，传感器节点之间组网的方式为自组织组织结构。拓扑控制和覆盖优化已成为无线传感器网络研究的核心问题，它决定了传感器的规模网络的感知与监测能力，直接反映了无线传感器的服务质量。为了在尽可能减少无线传感器网络覆盖盲区的同时，提升传感器节点获取信息的能力，必须对传感器节点进行合理有效的部署。近年来，无线传感器网络的研究发展迅速，其研究热点是通过拓扑控制和覆盖优化策略实现资源的优化配置。即使在计算能力、节点能量和通信带宽不满足条件的情况下，也能达到提升监测与通信等服务质量的目的，从而延长网络寿命。

覆盖增强和拓扑控制是基于无线传感器网络的目标监测应用中的关键问题。该问题以覆盖性能或网络寿命作为评价网络服务质量的主要标准，通过优化网络的部署和拓扑结构来提升无线传感器网络的整体监测能力。这一问题直接关系到无线传感器网络为特定监测任务所提供的有效监测质量和持续时间。目前，已有研究成果存在未考虑网络异质性、算法收敛至局部极值以及应用场景单一等问题。因此，有必要根据无线传感器网络的特点及具体应用场景，设计合理且高效的覆盖增强算法和拓扑控制方案。

相关工作

近年来，国内外许多学者对无线传感器网络的覆盖优化进行了研究。拓扑控制和最优覆盖的主要目的是提高网络效率、均衡能量消耗以及增加网络覆盖范围。常用的方法包括功率控制和分层拓扑设计，以优化通信链路，降低能量消耗并提升无线传感器网络的性能。近年来，众多专家和学者围绕优化网络覆盖开展了大量研究，旨在延长网络寿命、提高覆盖范围、增强鲁棒性、降低能量消耗以及减少链路故障。Za´ rraga‐Rodrı´guez 等人提出了一种新策略，通过将具有基本拓扑结构的小型网络相结合，实现大量无线传感器之间的分布式一致性连接，并实现低功耗。克萨基斯等人采用非均衡能量分配算法，通过节点布置提供尽力覆盖拓扑控制原理，构建了一个优化问题，并定义了一个结合网络覆盖率和生命周期的目标函数。赫德尔等人提出了一种用于无线传感器网络的覆盖感知高效平面面拓扑结构（CAFT），该设计有效降低了能量消耗，从而延长了无线传感器网络的生命周期。为应对传感器连通性和覆盖中的不确定性，塞努西和梅卢克设计了一种基于概率的通信成本模型，并利用信度函数理论定义了一种通用的证据融合方案，以捕捉现实应用中的多种特性。他们考虑了推导无线传感器网络中连通性与覆盖最优条件的问题。大多数此类问题属于非确定性多项式（NP）完全问题，阿尔‐卡拉基 和加万梅针对聚类结构在广义无线传感器网络中对连通性与覆盖的影响及其路由作用进行了动态规划研究。拉马扎尼等人提出了一种新颖的集中式方法，用于在无坐标网络中检测并相对定位无线传感器网络的覆盖空洞，构建了等效空洞平面图，该图与原始传感器网络图具有相同数量和位置的空洞，同时保持了嵌入特性。贾米伊等人提出了一种基于非支配排序遗传算法和学习自动机（LA）的自适应多目标优化框架，用于异构无线传感器网络中的覆盖和拓扑控制。李等人提出了一种小概率变异替换策略，用于在搜索过程中替换不满足覆盖要求的个体，并改进了适应度函数，使得可通过调整改进后适应度函数中的参数来调节网络密度。为了以最小的能量消耗实现更高的面积覆盖率并加快收敛速度，提出了基于边的质心（EBC）算法，以在分布式网络中提高面积覆盖率并实现更快的收敛速度。

智能算法是一种无需集中控制的优化算法。该算法结构简单，易于理解和实现。群体智能优化算法在信息监控与控制优化中起着非常重要的作用。在提高生产效率的同时，也最大程度地节约了网络资源。为了设计一种轻量级且高效的传感器布置算法，Senouci等人提出了结合二进制粒子群优化（PSO）特性和无线传感器网络部署要求的方法。所提方法的有效性和效率通过大量仿真进行评估。为了在保证服务质量的基础上最大化网络覆盖率并最小化能耗，提出了一种无线传感器网络覆盖优化方法基于改进的人工鱼群算法（AFSA）提出了一种方法。为了监测目标区域并获取有效数据，本文提出了一种基于改进的鲸鱼算法的无线传感器网络覆盖优化模型，该提出的算法能够有效提高无线传感器网络中节点的覆盖，并优化网络性能。

由于实际工程中遇到的问题复杂多变，且存在多种约束条件，因此建立相应的模型非常困难，寻找符合工程实践的智能优化方法显得尤为重要。这也是许多学者采用智能优化算法解决实际问题的原因之一，同时也是研究热点。因此，本文提出了一种基于狼群优化算法的无线传感器网络拓扑控制与最优覆盖方法，该方法能够提高网络的覆盖和工作效率，并延长网络寿命。

阐述了拓扑优化与覆盖的相关问题，以及狼群优化算法在无线传感器网络拓扑结构中的应用。具体包括无线传感器网络最优覆盖的拓扑建模，以及基于狼群优化算法的无线传感器网络拓扑结构与最优覆盖的优化设计。并通过实验仿真将狼群优化算法与粒子群算法和人工鱼群算法进行对比，验证了狼群优化算法在无线传感器网络覆盖优化问题上，对于提高网络覆盖、降低能量消耗以及改善网络寿命方面均有显著提升。

本文其余部分组织如下。第“最优覆盖问题的拓扑优化”部分是对拓扑优化中最优覆盖问题的数学建模。第“WPA”部分是狼群算法（WPA）的数学建模及详细实现过程。第“WPA在无线传感器网络拓扑结构优化中的应用”部分介绍了WPA在无线传感器网络拓扑结构优化中的应用。仿真分析与讨论在“算法仿真比较与结果分析”一节中给出。第“结论”部分给出了结论。

拓扑优化的最优覆盖问题

作为研究的基本模型，二维感知模型在无线传感器网络中被广泛使用。它具有结构简单、问题求解难度低的特点。在一个感知半径为r的节点中，半径的大小完全取决于感知源的固有物理特性。目标节点能被检测节点感知的条件是，该目标节点位于以检测节点为中心、半径为r的感知圆内。图1展示了基本的布尔感知模型。在传感器节点感知半径内的目标节点被感知概率为100%，而在外部的感知概率为0%。

为了更直观地表达狼群优化算法的优越性和有效性，实验基于二元感知模型设置了一个覆盖平面。该平面上有M个传感器节点，传感器节点的通信半径和感知半径分别为r和R。每个传感器节点的坐标设为(xl, yl)，所有二维覆盖平面上的传感器节点集合表示为O={O1, O2, O3,…, OM}。设平面上任意一点Rt的坐标为(xt, yt)，则传感器节点到任意点的距离表示为

$$
d(O_l, R_t) = \sqrt{(x_l - x_t)^2 + (y_l - y_t)^2}
\quad (1)
$$

传感器节点Ol对目标节点的测量率为

$$
C_p(O_l, R_t) =
\begin{cases}
1, & d(O_l, R_t) \leq r_o - r_e \
e^{-\partial d(O_l,R_t)}, & r_o - r_e < d(O_l, R_t) < r_o + r_e \
0, & d(O_l, R_t) \geq r_o + r_e
\end{cases}
\quad (2)
$$

在二维检测平面上，目标节点位于Ol 覆盖的坐标为(x, y)的节点，且覆盖率表示为

$$
C(x, y, o_l) = 1 - \prod_{t \in l}(1 - c(x, y, o_t))
\quad (3)
$$

假设覆盖区域为I，其面积表示为a × b，网络的覆盖由网格中心的覆盖表示。参数f1(xl, yl) 是传感器的面积覆盖率网络（覆盖区域(I)）和网络的有效覆盖。参数 f2(xl, yl) 是节点利用率 (SenRat(I)) 和反应工作节点数量。

为了确保网络覆盖率最大化且节点利用率最小化，通过设置适应度函数对子目标函数 f1(x) 和 f2(x) 进行加权转换，得到总体目标函数。目标函数如下

$$
f_1(x_l,y_l) = \frac{\int_0^a \int_0^b C(x,y, o_l)dxdy}{a \times b}
\quad (4)
$$

$$
f_2(x_l,y_l) = \frac{\sum_{l=1}^m C(x_l, y_l)}{a \times b}
\quad (5)
$$

$$
f(x) = v_1 f_1(x_l,y_l) + v_2 f_2(x_l,y_l)
\quad (6)
$$

在公式(4)中，参数$\int_0^a \int_0^b C(x,y, o_l)dxdy$表示传感器工作节点的有效覆盖面积，参数$\sum_{l=1}^m C(x_l, y_l)$表示传感器区域内的工作节点数量。参数v1和v2分别是f1(x)和f2(x)的权重，且v1+ v2= 1，(v1, v2 ∈ [0,1])。优化目标函数f(x)的值越大，说明节点部署方案越优。

WPA

WPA 是由吴HS、张FM等学者于2013年提出的一种仿生优化算法，用于模拟狼的捕猎行为。该算法借鉴了自然界中狼群的捕猎与食物分配机制，以人工狼为主体，采用基于责任分工的协同路径搜索结构，将工程优化求解过程抽象为狼捕猎的五个阶段：侦察狼、狼嚎、狼攻击、群体围攻和淘汰更新。

与其他群体智能算法相比，WPA具有更好的局部搜索和全局优化能力，更强的优化稳定性，以及更具竞争力。

狼的分工

根据不同的适应度值，人工狼可分为三类：头狼、猛狼和侦察狼。其中，头狼具有最敏锐的嗅觉和最佳的适应性，代表最优解的位置。侦察狼通常有多个，嗅觉较好，适应度仅次于头狼。它们经常在最优位置周围的多个方向进行探索，并随机改变根据适应度的变化调整它们的身份，从而增加了优化算法的随机性和精度。猛狼嗅觉较差且数量众多，代表攻击主力，促使算法收敛到全局最优。捕获猎物后，狼群不会平均分配食物，而是按照“按劳分配，论功行赏”的原则进行分配：首先将食物分配给贡献最大的狼，然后分配给侦察狼，其余部分由狼群共同分配。这种残酷的优胜劣汰规则保障了狼的生存与繁殖。在 WPA中，每轮狩猎结束后，若干适应度值较差的狼会被淘汰，同时随机生成相同数量的人工狼，以确保算法收敛的精度。

算法描述

使用WPA解决优化问题可以通过狼群狩猎过程进行形象描述。首先，释放狼群进行全局搜索，并选择嗅觉到食物气味最浓的狼作为头狼（适应度最佳，其值为Xb）。选取适应度值仅次于头狼的Q只狼作为侦察狼（适应度值Xi，Xi < Xb），其余均为猛狼（适应度值 Xm，Xm < Xi）。每只侦察狼可在P个方向上进行局部搜索。在游走过程中，若其适应度值大于头狼，即Xi > Xb，则该狼被视为新头狼（Xb=Xi）；否则返回原始位置并继续搜索。其次，狼发送信号。当猛狼发起奔跑时，它会向适应度最佳的位置靠近，并冲向距离头狼dm的位置（dm < dmin）。在袭击过程中，若猛狼嗅到的食物气味浓度超过头狼（Xm > Xb），则猛狼转变为头狼并发送信号。随后，猛狼与侦察狼对猎物发起围攻，并根据狩猎结束后个体所感知的新猎物食物气味浓度的变化，决定是否更新位置。最后，将人工狼按适应度值降序排列，淘汰若干适应度较差的狼，保留剩余的R只狼进入下一代，开启新一轮的狩猎操作。

群体行为和规则描述

狼群的捕猎过程分为五个阶段，每个阶段的行为都符合自然的生存法则，体现了群体智慧分工与合作，且均具有固定的更新规则：

1. 头狼更新规则 ：在初始计算中，选择适应度最佳的狼作为头狼。在WPA的每次迭代后，将当前具有最佳适应度的狼的适应度值与前一头狼的适应度值进行比较。如果当前狼的适应度更优，则更新头狼的身份和位置；否则，头狼的位置保持不变。如果有多个狼同时具有最佳适应度，则随机选择其中一匹作为头狼。头狼仅发出围攻信号，不参与具体的优化过程，直到下一次迭代被替换为止。

2. 侦察狼的游走行为 ：假设整个狼群中有N只狼，其中Q只侦察狼，参数Q随机选择为[N/(a+ 1)和 N/a],之间的整数，参数a为狼检测尺度因子。侦察狼转变为头狼的机制如上所述。如果侦察狼不需要更新为头狼，则其将独立决策，分别向P个方向各前进一步（该步长称为行走步长stept），记录前进后的适应度值并返回原始位置。在向第h个方向（h = 1, 2, 3,…, P）前进后，狼i在第d维的位置为

$$
x_{id}^h = x_{id} + \sin\left(\frac{2\pi h}{P}\right) \cdot \text{step}_d^t \cdot a
\quad (7)
$$

主动狼所在原始位置的适应度值为xi0。侦察狼从记录的P个适应度值中选择最优适应度值xi(xi > xi0)进行前进移动，并更新侦察狼的位置状态xi。该过程持续至侦察狼被更新为头狼或游走次数T达到最大值T max。由于个体差异，猎狼的搜索方向p各不相同。过大的p选择会提高搜索精度，但搜索速度较慢，因此通常在[pmin、pmax]之间随机选择。侦察狼的游走行为体现了狼群的智能分工与协作机制。

3. 猛狼奔跑行为 ：当Z只猛狼接收到头狼的围攻信号（Z = N − Q − 1）时，它们将迅速向头狼所在区域靠近，并保持较大的步骤大小步骤m。然后，第k次迭代后猛狼i在d维空间中的位置

$$
x_{id}^{k+1} = x_{id}^k + \text{step} d^m \cdot \frac{j_d^k - x {id}^k}{|j_d^k - x_{id}^k|}
\quad (8)
$$

在公式中，参数jkd表示狼群在第k次迭代时于d维空间中的位置。公式(8)可分为两部分：前一部分是狼 i在迭代前的位置基础，后一部分反映了头狼指令以及狼群趋向靠近头狼位置的趋向。在袭击过程中，猛狼转变为头狼。如果在袭击过程中无需转变为头狼，则猛狼i将冲向距离该狼dm的位置，并加入攻击队列 （其中dmin为限定距离，dm < dmin），参与群体围攻。假设待优化的第r个变量的取值范围为[minr, maxr]，则极限距离的估计值为

$$
d_{\text{min}} = \frac{1}{R} \cdot b \cdot \sum_{r=1}^{R} | \text{max}_r - \text{min}_r |
\quad (9)
$$

公式(9)中的参数R表示工程问题中所有待优化变量的个数，参数b表示距离确定因子。增大b的取值可以加快算法收敛，但过大会影响围攻行为，降低算法的精度。猛狼的攻击行为反映了狼群中高度发达的信息共享机制以及头狼的绝对领导和指挥作用。

4. 群体围攻行为 ：当猛狼冲入攻击范围时，联合检测狼会立即对猎物发起群体围攻。对于第k代狼群，头狼位置jkd 在d维空间中被近似视为猎物位置，狼的围攻行为可用公式(10)表示

$$
x_{id}^{k+1} = x_{id}^k + l \cdot \text{step} d^g \cdot (j_d^k - x {id}^k)
\quad (10)
$$

公式(10)中的参数l是一个在[−1,1],和g之间均匀分布的随机数，表示狼群发起围攻时的攻击步长。假设第 r个待优化变量的取值范围为[minr, max r] ，则侦察狼的游走步长stept、猛狼冲刺的步长stepm以及同一维度上狼攻击的步长stepg具有如下关系

$$
\text{step}_t = \frac{\text{step}_m}{2} = 2 \cdot \text{step}_g = \frac{|\text{max}_r - \text{min}_r|}{e}
\quad (11)
$$

公式（11）中的参数e表示步长因子，代表个体人工狼在搜索范围内优化的精细程度。

5. 淘汰与更新阶段 ：完成围攻行为后，人工狼根据适应度是否优化来决定是否更新当前位置。在算法中，依据自然界“优胜劣汰”规则，淘汰适应度较差的y只狼，并随机生成y只人工狼。y的取值也影响算法的优化性能。随着y值增大，狼群的个体多样性增加；但y值过大，会使搜索更加随机；y值过小，则会降低狼群开发最优空间的能力。在实际操作中，y通常在[N/2 ⋅ u, N/u],之间随机选择一个整数，参数u为种群更新因子。

基于WPA求解优化问题的算法步骤如下：

1. 种群初始化 ：初始设置总共N只人工狼，并将其随机分配到解空间中。设定相关参数：最大迭代次数为kmax，最大游走次数为Tmax，侦察狼比例因子为a，距离判定因子为b，种群更新因子为u，步长因子为e。初始化完成后，进入步骤2。

2. 选择头狼，侦察狼游走 ：选取当前适应度最优的人工狼作为头狼（其适应度值为Xb），并让Q只狼进行游走。在游走过程中，若侦察狼i的适应性优于头狼，即Xi > Xb，则立即更替为头狼；否则保持游走状态，直至达到最大徘徊次数Tmax，然后进入步骤3。

3. 狼群发出捕猎呼唤并集体冲锋 ：当侦察狼完成游走后，狼群发出捕猎呼唤，猛狼根据公式(9)进行冲锋。在奔跑过程中，若猛狼m的适应度优于头狼的适应度，即Xm > Xb，则猛狼m转变为头狼；否则，它将奔跑到距离头狼dm的一个位置，然后进入步骤4。

4. 群体围攻 ：猛狼和侦察狼按照公式(10)所述方式对猎物发起围攻。围攻完成后，转至步骤5。

5. 淘汰更新 ：人工狼根据当前位置的适应度值判断是否更新位置。淘汰y只适应度较差的人工狼，随机生成y只人工狼，完成种群替换，然后进入步骤6。

6. 终止判断 ：判断所请求的优化解是否满足精度要求或达到最大迭代次数kmax。如果满足，则算法终止；否则，返回步骤2。WPA的流程图如图2所示。

WPA在无线传感器网络拓扑结构优化中的应用

在实际应用环境中，为了确保传感器节点能够覆盖整个区域，研究人员通常需要布撒大量传感器节点，并通过高密度节点布撒来保持网络的高覆盖率。但从经济性和能效的角度来看，传感器节点存在高成本和能量有限的缺点。因此，关于网络最优覆盖的研究是无线传感器网络领域的一个研究热点。由于无线传感器网络具有动态拓扑变化、能量约束和传输距离有限等特点，合理的网络覆盖能够有效分配网络空间资源，更好地完成环境感知和信息获取等任务，而当前无线传感器网络的覆盖方法尚不能完全覆盖传感器网络。

基于无线传感器网络拓扑结构的基本特征，本文构建了人工定义，并在特征条件的约束下对其进行优化。同时，采用分层拓扑结构作为无线传感器网络拓扑的基本结构。在对该结构进行详细分析的基础上，提出了一种高效节能的自动拓扑控制算法。簇头在固定周期内以相同概率随机选择，从而使传感器节点均衡分担无线传感器网络的整体能耗，确保簇内成员的节点数据实现均衡分布，并完成无线传感器网络拓扑结构的优化设计。该算法能够满足数据延迟的要求，提高网络的覆盖，保障数据传输的安全稳定。

无线传感器网络的拓扑优化设计和覆盖优化步骤如下：

1. 设置算法参数。设置无线传感器网络传感器节点的覆盖模型参数，生成传感器节点的初始位置，并根据目标函数计算网络的覆盖。狼群规模为N，最大迭代次数为Maxgen，最大徘徊次数为Tmax，侦察狼检测尺度因子为a，距离判定因子为b，种群更新因子为u，步长因子为e。

2. 在初始种群中，选择猎物气味浓度最大的头狼作为侦察狼，以及排除最佳的狼第一只狼被用作侦察狼。根据公式(7)，它将持续游走，直到侦察狼的气味浓度大于头狼的气味浓度，或达到最大徘徊次数Tmax。

3. 进入召唤行为。猛狼冲刺并靠近头狼，使用公式 (8)计算冲刺后的状态。如果在袭击过程中猛狼嗅到的猎物气味集中在该狼身上，则该狼替换为头狼并执行召唤行为。否则，猛狼持续向头狼方向冲刺距离dm。

4. 进行围攻行为。人工狼参与围攻行为使用公式(10)在围攻后更新其位置。

5. 对狼群中的个体进行排序，选择最佳个体作为头狼，然后更新头狼的位置。种群按照狼的再生模式进行更新。

6. 确定终止条件算法的条件得到满足。如果满足，则输出最优解，算法结束；否则，转到步骤2。

最后，基于狼群优化算法实现了无线传感器网络的拓扑优化，提高了网络的覆盖和网络的工作效率。

算法仿真比较与结果分析

本文的仿真环境基于MATLAB 2017a，对WPA、PSO和AFSA的性能进行了比较。仿真结果表明，在拓扑结构的优化设计中，WPA在节点的平均剩余能量、平均传输延迟、平均分组投递率、网络覆盖以及存活节点数量等指标上均明显优于PSO算法和人工鱼群算法。在本文设定的仿真环境中，传感器节点感知数据的能量消耗、接收数据的能量消耗、发送数据的能量消耗、平均传输延迟和平均分组投递率的计算公式如下

$$
E_S = l \cdot e_s
\quad (12)
$$

$$
E_{N-R} = l \cdot e_r
\quad (13)
$$

$$
E_{N-T} =
\begin{cases}
l \cdot E_{\text{elect}} + l \cdot j_{fs} \cdot d^2, & d < d_0 \
l \cdot E_{\text{elect}} + l \cdot j_{mp} \cdot d^4, & d \geq d_0
\end{cases}
\quad (14)
$$

$$
F_a = \frac{P_{Fr} + F_p - F_n}{N}
\quad (15)
$$

$$
R_{\text{gad}} = \frac{T_{\text{rdp}}}{T_{\text{sdp}}}
\quad (16)
$$

在公式（12）中，参数es为 $60 \times 10^{-9}$ 焦耳/比特，在公式（13）中，参数er为 $135 \times 10^{-9}$ 焦耳/比特，在公式（14）中，参数jmp为 $0.0013 \times 10^{-12}$ 焦耳/比特/米，4为多径传输参数，参数jf s为 $10 \times 10^{-12}$ 焦耳/比特/米，2为普通空间传输参数。控制包长度为200比特，参数E elect 为 $45 \times 10^{-9}$ 焦耳/比特，参数l表示发送数据包的数据长度，且参数l为4000比特。阈值d0 为 87米，初始能量E0 为1焦耳。表2显示了仿真环境参数。

为了算法仿真结果的可靠性，本文的仿真结果是在多次实验后获得的算法平均运行100次。在公式（15）中，参数Fa是平均传输延迟，参数Fr是前一个数据包的传输时间，参数Fp的数据处理时间，以及参数Fn到达下一跳的到达时间。在公式（16）中，参数Rgad是平均分组投递率，参数Trdp是接收数据包总数，参数Tsdp是发送数据包总数。

算法覆盖效果比较

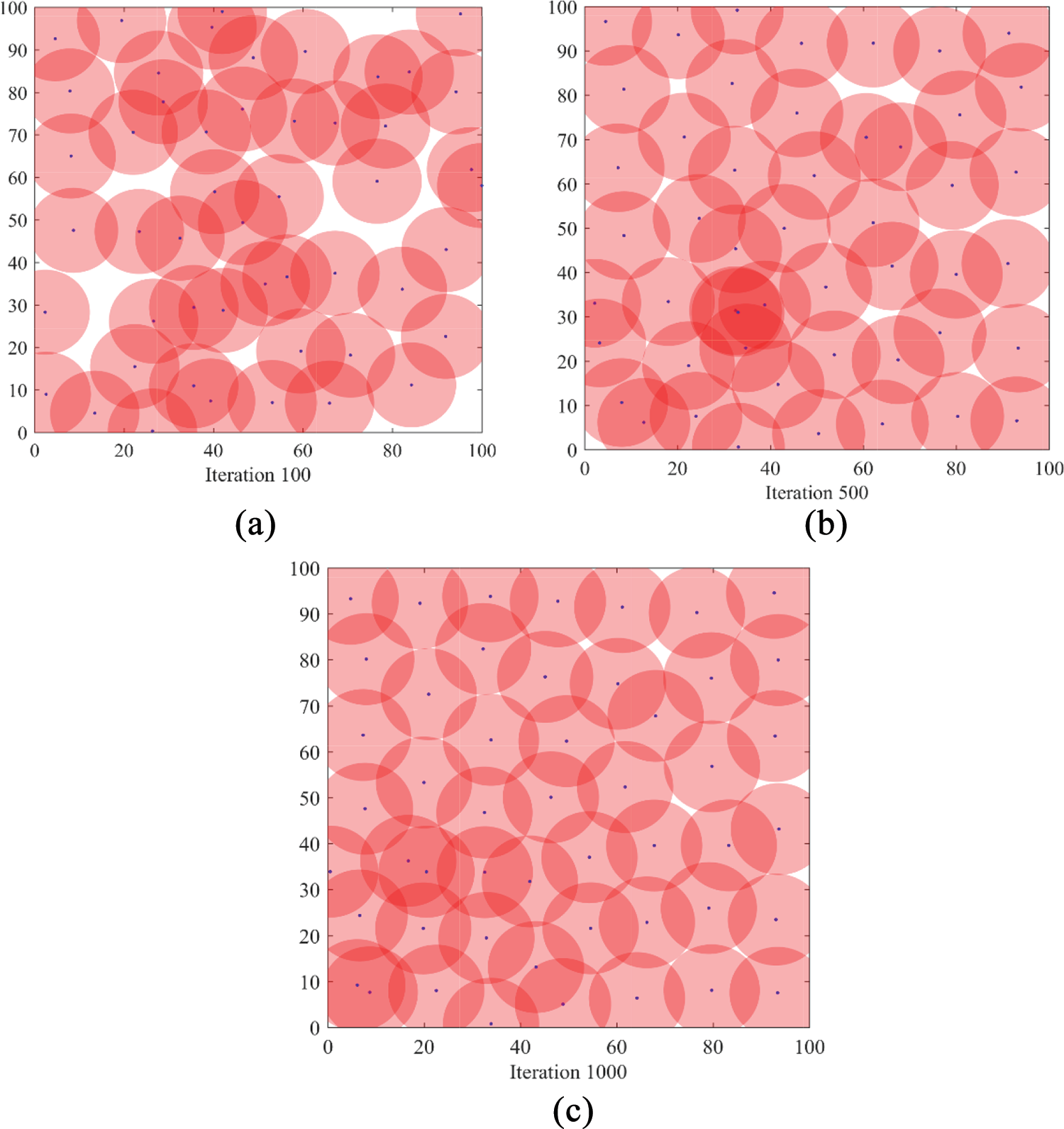
为了验证狼群优化算法的覆盖效果，在所有节点具有相同感知半径的同构网络中进行实验。为了比较和分析PSO算法、人工鱼群算法和WPA的覆盖性能，采用相同的仿真条件。首先，在监测区域中随机生成传感器节点位置。图中，方形框表示被覆盖的监测区域，“×”表示传感器节点位置，圆形表示节点的覆盖区域。图3–5分别显示了经过PSO算法、人工鱼群算法和WPA优化后传感器节点的最终位置。

对比三种节点分布图可以发现，经过PSO算法优化后相比初始条件有一定改善，但节点分布非常不均匀，仍然存在大量盲区和重复覆盖区域。经过AFSA优化后，节点分布比PSO更均匀，覆盖死区和重复覆盖区域有所减少，但仍未达到理想的覆盖效果。经过WPA优化后，节点分布更加均匀，覆盖盲区和重复覆盖区域相对更少。从分布图可以看出，WPA的分布效果明显优于PSO算法和AFSA。

节点的平均剩余能量

节点的平均剩余能量是重要指标之一，用于评估传感器网络拓扑部署机制是否优越。一个好的拓扑部署机制可以增加传感器节点的剩余能量，从而有效延长网络生命周期。WPA、PSO算法和人工鱼群算法在节点平均剩余能量方面的仿真结果如图6所示。

图6显示了PSO、人工鱼群算法和WPA三种算法下传感器节点的剩余能量。WPA和人工鱼群算法节点的平均残余能量高于PSO算法。本文算法对拓扑结构优化后的传感器网络节点具有最高的残余能量，且随着时间增加，残余能量消耗相对较慢。

平均传输延迟

无线传感器网络对数据传输的实时性和有效性有较高要求。这要求数据从源节点传输到目的节点以克服路径拥塞、链路故障、节点能量消耗和数据传输速率等诸多问题，确保传输延迟尽可能低。三种算法的平均传输延迟比较如图7所示。

从图7可以看出，本文提出的WPA部署策略相比AFSA和PSO算法显著降低了平均传输延迟，而基于粒子群算法的部署策略效果最差。这是因为狼群优化算法中的受限竞争策略极大地提高了子群寻找最优解的速度，同时避免了陷入局部最优。相反，粒子群算法由于过于倾向于直接寻找全局最优，导致分工失衡而陷入局部最优。由图7可知，本文算法的平均传输延迟在0.14之间分别为0.17秒，最低可达0.14秒。人工鱼群算法在0.16到0.20秒之间，粒子群算法的平均传输延迟在0.18到0.22秒之间。大量实验数据表明，本文提出的WPA在数据传输的各个方面均优于PSO算法和人工鱼群算法。

群体平均投递率

平均分组投递率是指接收到的数据包总数与发送的数据包总数之比，该值的大小直接反映了数据传输的可靠性。平均分组投递率越高，丢包率越低，无线传感器网络的数据传输性能越稳定。图8显示了三种算法的群体平均投递率比较结果。

从图8可以看出，在通信半径增大的过程中，PSO算法、AFSA和WPA的分组投递率差异越来越明显。尽管都在下降，但本文提出的WPA的分组投递率下降最慢。当通信半径为35 m时，PSO算法的平均分组投递率仅为42%，AFSA为50%。本文提出的WPA仍保持较高的投递率，达到56%。

网络覆盖率

网络的覆盖是评估拓扑结构质量的重要参数。当传感器感知范围一定时，部署方法是否最有效决定了网络覆盖率能否最大化。三种算法的网络覆盖率比较如图9所示。

从图9可以看出，本文提出的WPA的收敛速度优于PSO算法和人工鱼群算法。并且从图10发现，随着迭代次数的增加，网络的覆盖逐渐趋于平缓。这表明该算法的收敛速度得到加快。本文提出的算法与PSO算法、人工鱼群算法相比，网络平均覆盖率分别提高了约10.5%和5.6%。同时，本文提出的WPA能够在较少的迭代次数下找到最优解。与其他算法相比，响应时间缩短，稳定性显著提高。

存活节点数量

无线传感器网络中的传感器节点具有大规模部署和覆盖范围广的特点。因此，存活节点数量越多，网络传输性能越好。随着时间的推移和节点能量的消耗，许多传感器节点将会失效。因此，有必要增加网络节点的存活数量。图10显示了三种算法中存活节点的数量。

如图10所示，可以看出整个传感器网络中存活节点数量随时间的推移而减少。PSO算法在约100次轮询次数时出现节点失效现象，在600次轮询次数时存活节点数仅为35，存活率为70%。人工鱼群算法和本文算法均在约200次轮询次数时才开始出现节点失效。在600次轮询次数时，人工鱼群算法存活节点为38个，存活率为76%。本文提出的WPA仍有43个节点存活，存活率仍可维持在约86%。通过三种算法存活节点数量的对比可知，本文提出的无线传感器网络拓扑优化具有最长的网络生命周期。

从上述仿真结果可以看出，本文提出的基于WPA的无线传感器网络拓扑优化方法在性能上优于PSO算法和AFSA，具有更长的网络寿命、更低的能量消耗以及更好的网络覆盖率。

结论

针对工业应用领域中无线传感器网络的拓扑结构、部署方法中覆盖质量低和网络生命周期短等亟待解决的问题，提出了一种基于WPA的面向覆盖的策略的无线传感器网络新型拓扑优化方法。该提出的算法充分利用狼群优化算法的极限竞争策略特性，对传统智能优化算法，并利用部署策略提高无线传感器网络的能量利用率并增加网络覆盖。仿真结果表明，本文采用的狼群优化算法是有效且可靠的，能够更好地解决工业生产和温室农业中无线传感器网络的覆盖优化等相关问题。在未来的工作中，将狼群优化算法及其改进方法应用于移动无线传感器网络和异构无线传感器网络的拓扑优化设计方向仍需进一步研究。