简化进位保留加法器的阵列乘法器设计

基于简化进位保留加法器的阵列乘法器方案与电路设计

宋佳* †，吕世功，李夏雨，刘莉和何延东
微电子器件与电路教育部重点实验室，北京大学微电子研究所，中国北京100871

摘要

本文对基于进位保存加法器的传统阵列乘法器进行了优化。在用于部分积累的加法器数组中，某些特定的全加器被简化而无需付出任何代价。通过修改两个特殊全加器的逻辑表达式，降低了电路复杂性，从而减少了功耗和传播延迟。提供了加法器的静态电路结构以证明其有效性。此外，产生部分积的逻辑与门被重新设计以节省面积和功率。阵列乘法器的布局规则性得到了良好保持。
电路仿真显示，对于4*4结构，速度和功率分别提高了9.7%和3.1%，晶体管数量减少了5.3%。版权所有©2014约翰威立父子有限公司

2013年6月27日收到；2014年3月28日修订；2014年3月28日接受

关键词 ：阵列乘法器；进位保存加法器；部分积；高速；低功耗

1. 引言

乘法器广泛应用于当今的许多数字系统中，尤其是在数字信号处理器[1]中。乘法器的设计与实现方法对计算密集型超大规模集成电路系统[2–4]的面积、速度和功耗有重要影响。基于进位保存加法器（CSA）的阵列乘法器因其高性能和规则的布局而成为一种流行结构[5, 6]。

并行乘法包含两个步骤：部分积的生成以及它们的累加。部分积由被乘数与一个乘数位进行逻辑与操作得到。该逻辑操作是并行执行的。部分积累加步骤是一个多操作数加法，可以通过阵列或更复杂的树形结构实现。由于其规则的布局和简单的互连，阵列乘法器是最流行的架构之一。CSA阵列在无符号数乘法器中被广泛用于对部分积求和[7, 8]。树形乘法器速度快，但其复杂的结构导致更高的功耗，并且在VLSI布局中较难实现[9, 10]。

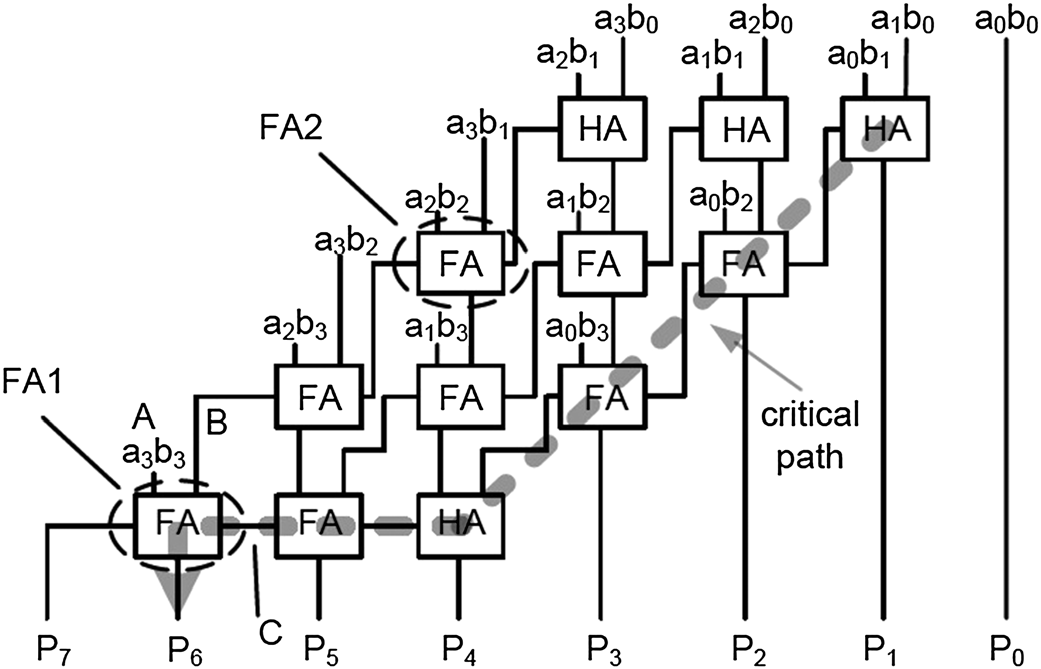
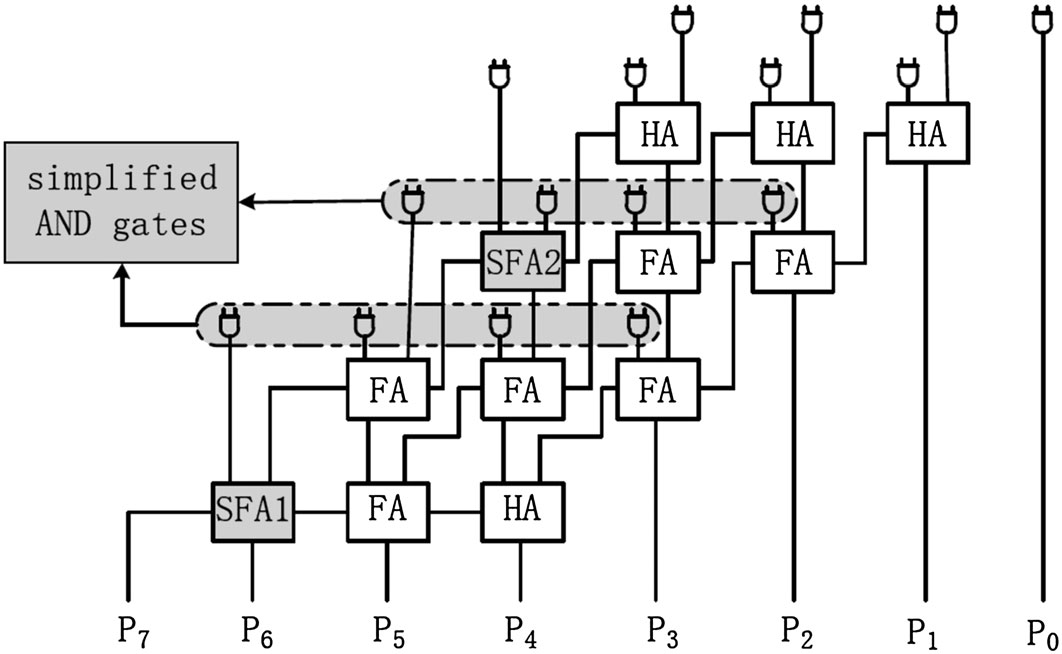
图1展示了4*4乘法器中用于累积部分积的CSA数组结构，其中FA代表全加器，HA代表半加器。加法器的输入为部分积，产生这些部分积的与门未在图中显示。CSA数组在累积完部分积后输出最终结果P1–P7。图1中显示了其中一条最坏情况下的关键路径。功耗可通过数组中所有加法器所使用的晶体管数量进行估算。CSA的面积由四行三列的加法器数组所占空间决定。

数组可以重新排列，并且可以利用动态电路来提升CSA乘法器的性能并减少毛刺[11–13]。这些电路较为复杂，可能不推荐用于实现。我们将在此展示，传统CSA结构可以被简化，以加速部分积累加并降低功耗。本信件安排如下：第2节是主要部分，介绍了主要思想；第3节展示了仿真和结果比较；最后，在第4节中做出简要结论。

2. 简化型进位保存加法器数组乘法器的设计

本节提出了用于实现CSA阵列乘法器的改进方案。首先，两个特殊的全加器被简化，详细内容将在第2.1节中说明。接着，在第2.2节中重新设计了与门阵列。这些新方案能够在不牺牲布局规则性或面积成本的前提下降低功耗和传播延迟。

2.1. 特殊全加器的简化

这里，我们定义A和B为全加器的输入，C为进位输入，S为和输出，Co为进位输出。Co和S的布尔表达式如方程(1)所示：

$$
Co = AB + BC + CA; \quad S = A \oplus B \oplus C = (A + B + C)Co + ABC \tag{1}
$$

半加器有两个输入A和B，一个进位输出Co，以及一个和输出S。它们的逻辑表达式在公式(2)中给出：

$$
Co = AB; \quad S = A \oplus B \tag{2}
$$

图1中圈出了两个全加器FA1和FA2。这些全加器是特殊的，因为它们的三个输入是相关的。部分积的数据依赖性使得重新设计这些全加器成为可能。

对于图1中的FA1，其输入为A= a3b3 , B和C。对于4×4无符号乘法器，最大乘积为15*15= 225或1111*1111= 11100001。如果a3或b3为0，则最大乘积为15*7= 105或1111*0111= 01101001。此时，最终乘积位P7为0，即FA1的进位输出。这意味着对于FA1，若A = a3b3 = 0，则其进位输出Co = 0。

由于Co = AB + BC + CA，我们可以推导出，若A = 0，则BC = Co = 0。该事实可表示为BC = ABC在逻辑上成立。显然，如果A = 1，我们仍然可以得到BC = ABC。通过将BC替换为ABC，方程(1)中的表达式可简化如下：

$$
Co = AB + BC + CA = AB + ABC + AC = A(B + C) \tag{3}
$$

$$
S = (A + B + C)Co + ABC = (A + B + C)Co + BC \tag{4}
$$

与方程(1)相比，上述FA1的表达式(3)和(4)更为简化。由于FA1位于CSA乘法器的关键路径上，因此简化的单元不仅能够节省功率，还能提高速度。

前述事实对于M*N乘法器同样成立。如果FA1的输入A = aM-1bN-1 = 0，它意味着在最大乘积时

$$
(2^{N-1}) \times (2^{M-1} - 1) = 2^{N+M-1} - 2^N - 2^{M-1} + 1 < 2^{N+M-1}
$$

或

$$
(2^{N-1} - 1) \times (2^{M-1}) = 2^{N+M-1} - 2^{N-1} - 2^M + 1 < 2^{N+M-1}
$$

在这种情况下，最高有效位PN+M−1为零，且简化的FA1也适用于CSA乘法器。显然，如果A = aM-1bN−1 = 1，我们仍然可以得到BC = ABC，且简化的FA1仍然适用于CSA乘法器。

对于图1中的FA2，我们将以相同的方式对其进行简化。输入可以表示如下：

$$
A = a_2b_2; \quad B = a_3b_1; \quad C = (a_2b_1) \cdot (a_3b_0) \tag{5}
$$

其中a2b2, a3b1, a2b1, 和a3b0是由一个被乘数位与一个乘数位进行逻辑与操作生成的部分积。此处我们可以将FA2的进位输入重写为：

$$
C = (a_2b_1) \cdot (a_3b_0) = (a_3b_1) \cdot (a_2b_0) = B \cdot (a_2b_0) \tag{6}
$$

并且根据方程(6)，我们可以将FA2的输出简化如下：

$$
Co = AB + BC + CA = A(B + C) + BC = AB + C \tag{7}
$$

$$
S = (A + B + C)Co + ABC = (A + B)(Co + AC) \tag{8}
$$

与方程(1)相比，上述表达式(7)和(8)更简单，因此所需器件更少，功耗更低。

利用我们对FA1和FA2的简化布尔方程，可以简化FA1和FA2的结构。图2所示为实现逻辑表达式(1)[7]的28‐T静态全加器电路方案。该全加器方案通常被称为镜像加法器，因其具有相同的NMOS和PMOS拓扑结构。它被认为是实现全加器逻辑[14]的最有效方法。在此，我们基于镜像加法器结构提出了实现FA1和FA2的方案。

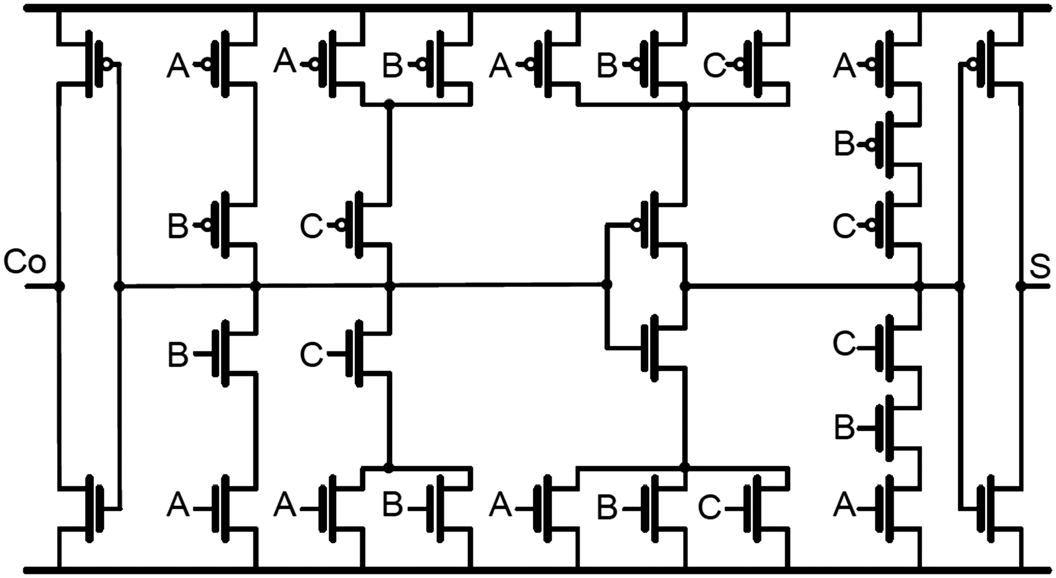
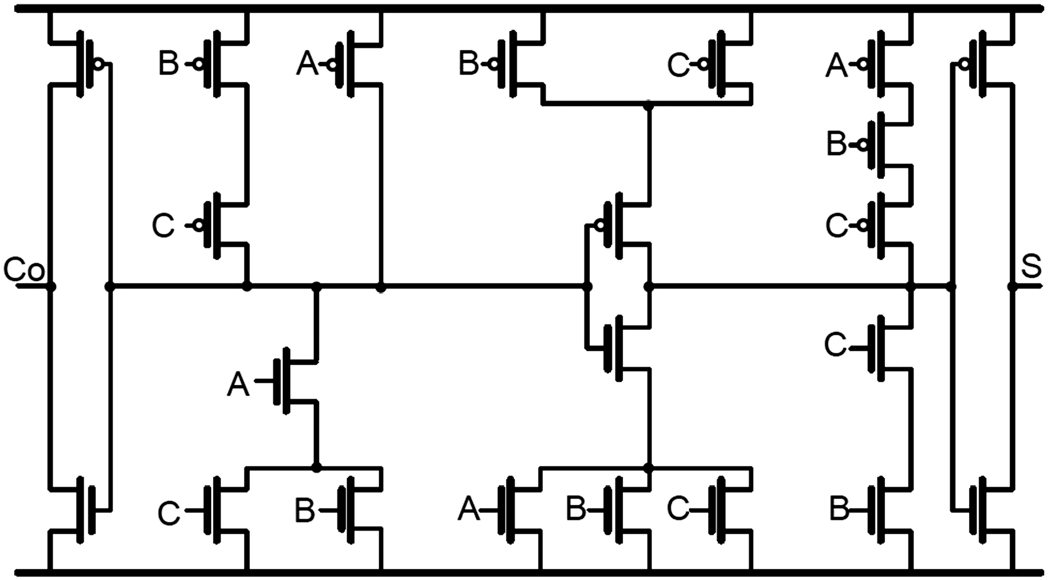
图3所示为图1中FA1的提出方案电路。对于输出S的逻辑，NMOS网络实现方程(4)中的表达式，而PMOS网络实现以下表达式：

$$
\overline{S} = \overline{A}(B + C) + \overline{Co} + \overline{BC} = \overline{A}(B + C) + \overline{Co} + \overline{BC}A(B + C) = \overline{A}(B + C) + \overline{Co} + \overline{BC} \tag{9}
$$

FA1电路有22个器件，因此比28T全加器更快且功率效率更高。由于FA1位于CSA的最关键路径上，有助于加速乘法操作。

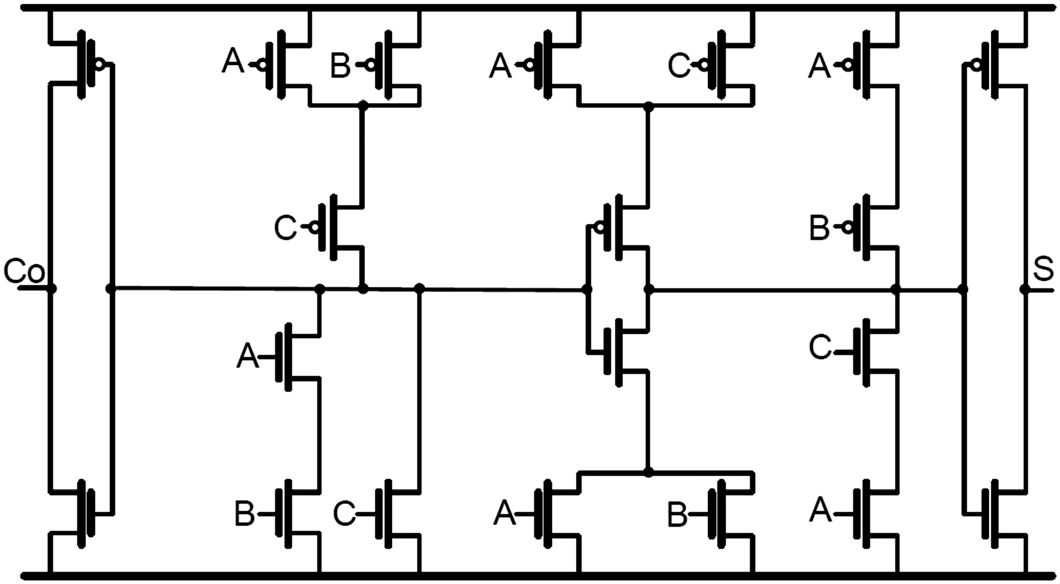
对于图4中的电路，它实现了公式(7)和(8)中的布尔表达式。输出Co的逻辑很容易理解。对于输出S的逻辑，NMOS网络实现了公式(8)中的表达式，而PMOS网络实现了一个变换后的表达式：

$$
S = (A + B)Co + AC = (A + B)(Co + AC) \tag{10}
$$

与28‐T全加器相比，FA2电路仅有20个器件，因此功耗更低。因此，由于简化的FA1和FA2，CSA的延迟、功率和器件数量均可降低。

2.2. 与门阵列的重新设计

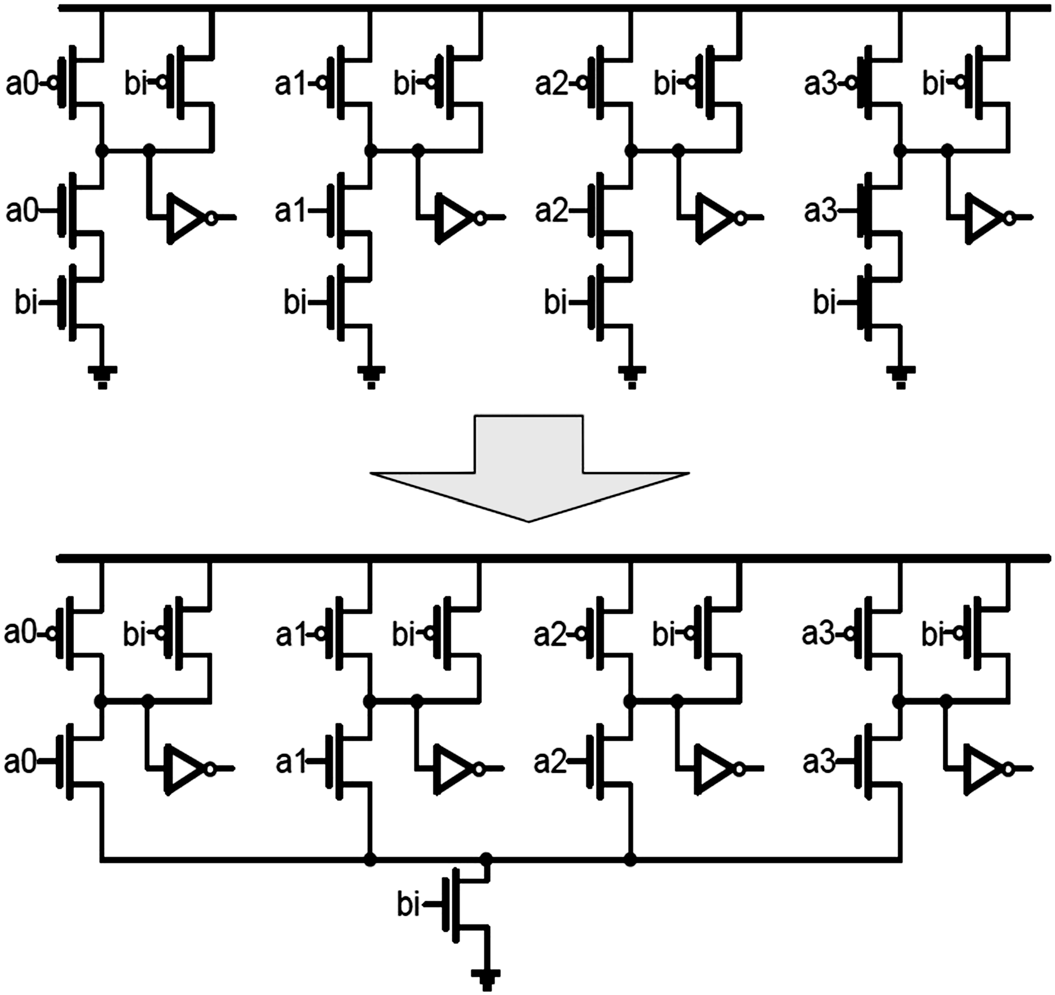
通常，乘法运算中的部分积由与门生成。因此，对于一个N*M乘法器，需要N*M个与门。由于一个互补金属氧化物半导体（CMOS）结构的与门包含六个MOS晶体管，因此构建N*M乘法器的与门阵列需要6*N*M个MOS晶体管。实际上，N*M乘法器的与门阵列可以划分为M行，每一行与门共享相同的输入信号，即乘数的一位。因此，这使得我们能够减少每行与门所需的MOS晶体管数量。以4*4乘法器为例，图5说明了提出方案。信号bi是乘数B[0的一位3],，它作为公共输入信号连接到四个与门。因此，原始与门中由bi控制的四个NMOS器件可以缩减为仅一个。

采用这种与门阵列缩减方案，器件数量得以减少，同时功耗也能降低。考虑到重构后的与门由于节点电容增大导致延迟增加，我们仅对不在关键路径上的与门进行重新设计。实际上，在N*M CSA阵列乘法器中，只有第一行和第二行的与门位于关键路径上。因此，我们可以保持前两行与门不变，而替换其余行。于是，对于一个N*M乘法器（其与门阵列为M行 N列），所提出的与门结构可节省(M−2)*(N−1)个NMOS器件，同时保持相当的延迟时间。

实际上，与阵列中的底部晶体管无需相应调整尺寸以维持延迟时间，因为重新设计的与门不在关键路径上，对整体延迟时间影响很小。然而，由于对称性的缺失，该设计在超大规模集成电路实现中的布局规整性有所降低。

最后，我们可以得到一个简化的CSA阵列乘法器，如图6所示，该乘法器采用了前文所述的两项改进。如图6所示，我们使用新型简化全加器SFA1和SFA2分别替代FA1和FA2，并且对不在关键路径上的与门进行了简化。可以看出，我们的设计保持了布局规则性，并且由于位于所有关键路径汇聚点的简化FA1，电路延迟将得以降低。同时，由于这些改进，器件数量和功耗均得到了节省。

3. 实验结果

HSPICE仿真结果包含本节的三个部分。首先，将提出方案的电路与其他典型的基于CMOS全加器的CSA乘法器。详细信息见表I。其次，在速度和功耗方面，将两种典型的阵列乘法器——传统阵列乘法器和跃 frog 阵列乘法器——与提出的CSA乘法器进行比较，结果如表II所示。在这两部分仿真中均采用4*4乘法器作为参考。最后，将N的数量从4增加到8和16，以观察提出电路的改进性能，结果如表III所示。使用HSPICE仿真器计算速度和功耗，并提供了晶体管数量作为参考。MOS器件模型参数来自中芯国际65纳米工艺（中国上海），电源电压为1 V。PMOS器件的阈值电压VthP为 −0.57 V，NMOS器件的阈值电压VthN为0.43 V。

从表I的结果中可以看出，我们的改进不仅适用于传统28‐T全加器，还可应用于其他 CMOS全加器阵列。与传统28‐T全加器、桥式全加器（BridgeFA）和高速全加器（HSFA）相比，所提出的电路不仅延迟改进最高可达9.7%、9.0%和6.9%，而且功耗降低最高可达 3.1%、5.7%和6.5%。

表I. 提出方案与其他基于CMOS全加器的CSA乘法器（4*4）的比较。
	原始CSA	提出的CSA	节省(%)
传统全加器
晶体管数量	376	356	5.3
延迟	0.5475纳秒	0.4949纳秒	9.7
功率	69.259μw	67.114μw	3.1
桥式全加器 [15]
晶体管数量	424	392	7.5
延迟	0.5407 纳秒	0.4918 纳秒	9.0
功率	74.490μw	70.241μw	5.7
高速全加器 [16]
晶体管数量	440	404	8.2
延迟	0.5021 纳秒	0.4674 纳秒	6.9
功率	75.320μw	70.453μw	6.5

表II显示了与传统阵列乘法器和跃 frog 阵列乘法器的比较。尽管提出方案电路的延迟改进不如跃 frog 阵列乘法器，但其功耗仍然远低于后者。此外，跃 frog 阵列通常需与华莱士树算法结合使用，在版图实现上较为复杂。

表II. 所提出的CSA乘法器与其他基于阵列的乘法器（4*4）的比较。
	传统数组[7]	Leap‐frog 数组[17]	所提出的CSA阵列
晶体管数量	376	432	356
延迟（纳秒）	0.5873	0.4507	0.4949
功率 (μw)	69.859	72.434	67.114

由于速度的提升主要源于关键路径中FA1的调整，因此随着具有更长关键路径的较大乘法器尺寸增加，延迟的改善百分比将下降。表III展示了诸如M = N= 8和M = N= 16等更大数组的改进变化情况。可以看出，速度提升从4*4乘法器的9.7%下降到16*16乘法器的0.45%。而功率和器件数量的减少则更为平缓，因为与阵列也随M和N的增加而增大。

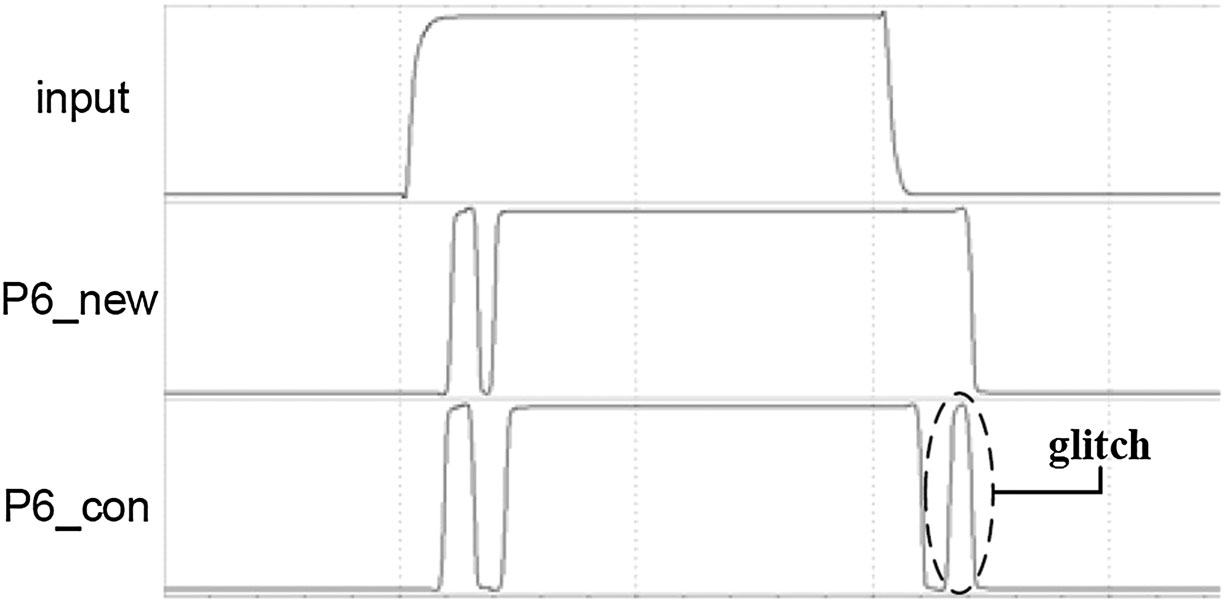
该芯片也经过了测试，输入向量在“1111”和“0000”之间切换时P6的输出波形如图7所示。实际上，从输入到P6的延迟代表了基于CSA的乘法器的最差延迟。在图7中，P6_new表示提出方案的简化CSA乘法器的输出P6，P6_con表示传统CSA乘法器的输出P6。可以看出，简化乘法器速度更快，且输出P6的毛刺更少。

仿真结果如表I所示。从结果中可以看出，简化电路使4*4乘法器的速度提高了9.7%，功率降低了3.1%（功耗延迟积降低12.4%），器件数量减少了5.3%。尽管在具有更长关键路径的更大规模乘法器中，改进百分比会有所下降，但考虑到在未引入任何面积开销的情况下同时提升了速度和功率，提出方案仍然值得推荐。

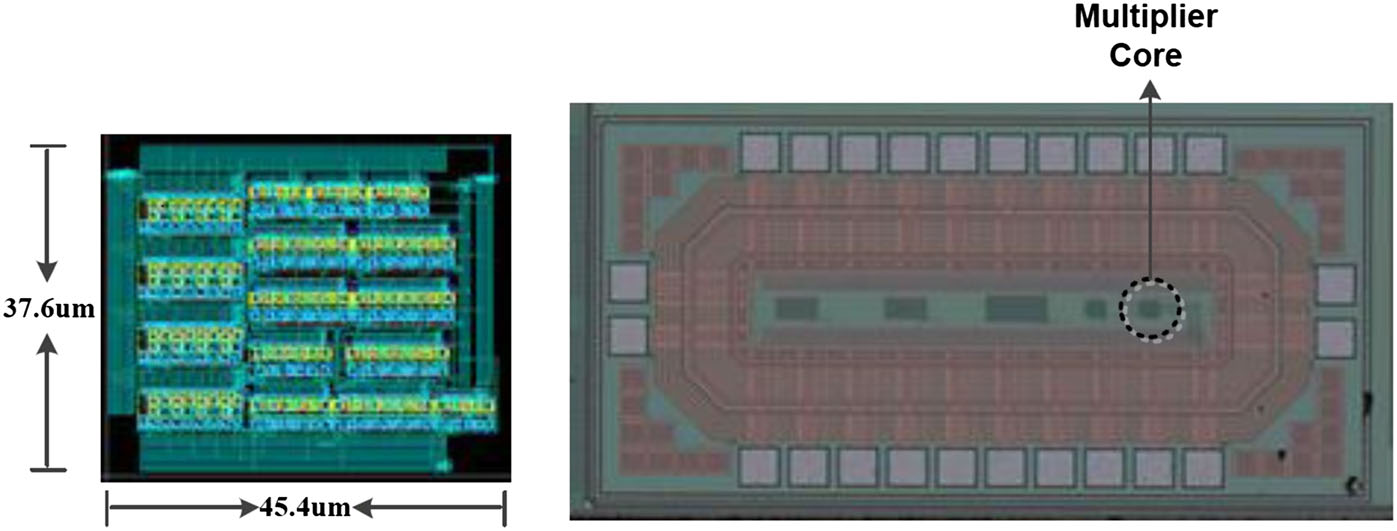
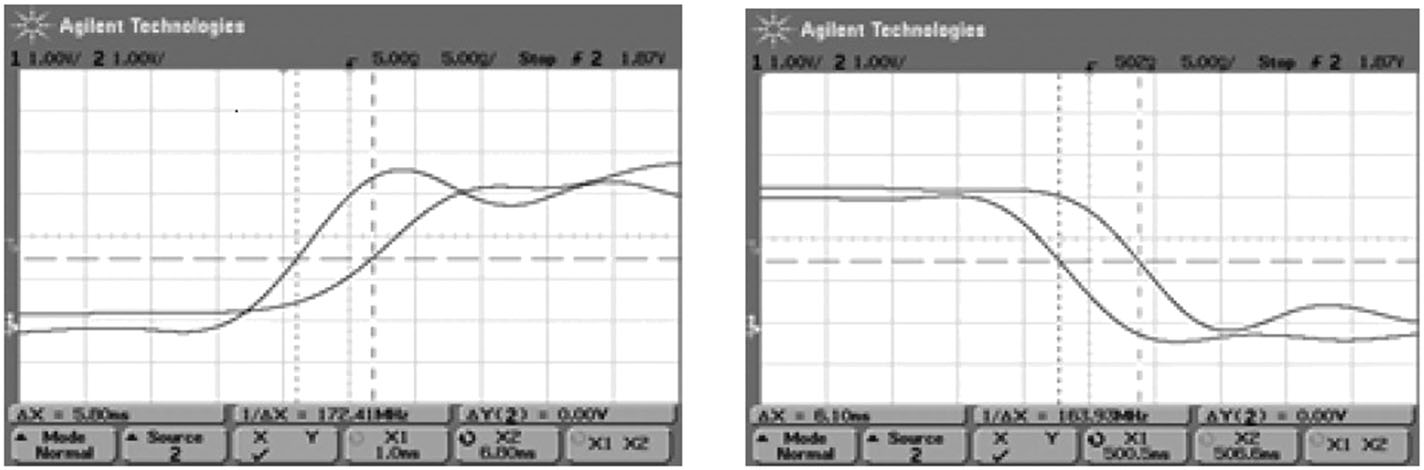
基于提出方案的4*4乘法器在中芯国际65纳米工艺上实现并制造。图8显示了布局和芯片照片。核心布局为37.6 μm*45.4 μm。芯片在安捷伦54622A示波器（美国加利福尼亚州圣克拉拉安捷伦科技公司）上进行测量。图9显示了输入信号切换后P6的实测上升和下降波形。实测上升和下降延迟分别为5.8和6.1ns。仿真与实测结果之间的差异是由输入输出单元的延迟以及测量设备和导线引入的RC延迟造成的。该假设通过HSPICE对带有输入输出单元的乘法器电路进行仿真，并在后面连接一个50‐Ω电阻和一个20皮法电容得到验证。乘法器芯片的实测功率为70.2 μw，与仿真结果一致。

表III. 提出方案与传统互补金属氧化物半导体全加器‐based N bit CSA乘法器的比较 r.
	传统全加器	提出方案	节省(%)
M = N= 4
晶体管数量	376	356	5.3
延迟	0.5475纳秒	0.4949纳秒	9.7
功率	69.259μw	67.114μw	3.1
M = N= 8
晶体管数量	2064	2008	2.7
延迟	1.2403 纳秒	1.2018 纳秒	3.1
功率	518.706μw	507.781μw	2.1
M = N= 16
晶体管数量	8480	8256	2.8
延迟	3.0721 纳秒	3.0583 纳秒	0.45
功率	2647.824μw	2612.549μw	1.3

4. 结论

建议一种简化的基于CSA的乘法器。两个全加器的布尔表达式被简化。与门中一些不在关键路径上的NMOS器件被合并。基于CSA乘法器的速度、功率和晶体管数量均得到改善。仿真表明，新电路优于传统的CSA乘法器，适用于超大规模集成电路设计。