基于Matlab的扩展卡尔曼滤波（EKF）实践

原创于 2025-12-18 18:15:00 发布 · 452 阅读

9 ·

CC 4.0 BY-SA版权

文章标签：

#音视频

基于matlab的扩展卡尔曼滤波（Extended Kalman Filter，EKF），通过卡尔曼滤波算法近似计算系统的状态估计值和方差估计值,对信号进行滤波。程序已调通，可直接运行。程序保证可直接运行。

在信号处理的领域中，扩展卡尔曼滤波（Extended Kalman Filter，EKF）是一种极为有用的工具，它能帮助我们对非线性系统的状态进行有效的估计。今天就来聊聊基于Matlab实现EKF对信号进行滤波的过程。

EKF原理简述

EKF本质上是卡尔曼滤波在非线性系统中的拓展。卡尔曼滤波主要是通过预测和更新两个步骤，不断地优化系统状态估计值和方差估计值。而在非线性系统里，我们没办法直接使用传统卡尔曼滤波的线性模型，所以EKF通过对非线性函数进行一阶泰勒展开近似线性化，以此来应用卡尔曼滤波的框架。简单来说，就是在每个时刻对系统的非线性模型进行局部的线性近似，从而能够像传统卡尔曼滤波那样计算状态估计和方差估计。

Matlab 代码实现

% 模拟非线性系统参数设置
dt = 0.01; % 时间步长
A = [1 dt; 0 1]; % 状态转移矩阵
H = [1 0]; % 观测矩阵
Q = [0.001 0; 0 0.001]; % 过程噪声协方差
R = 0.1; % 观测噪声协方差

% 初始化状态和协方差
x_hat = zeros(2,1); % 初始状态估计
P = eye(2); % 初始协方差估计

% 模拟生成真实状态和观测数据
N = 1000; % 数据点数量
x_true = zeros(2,N);
z = zeros(1,N);
x_true(:,1) = [0; 0];
for k = 2:N
    x_true(:,k) = A * x_true(:,k-1) + sqrtm(Q) * randn(2,1); % 生成真实状态
    z(k) = H * x_true(:,k) + sqrt(R) * randn; % 生成观测数据
end

% EKF 实现
x_hat_hist = zeros(2,N);
x_hat_hist(:,1) = x_hat;
for k = 2:N
    % 预测步骤
    x_hat_minus = A * x_hat;
    P_minus = A * P * A' + Q;
    
    % 计算卡尔曼增益
    K = P_minus * H' / (H * P_minus * H' + R);
    
    % 更新步骤
    x_hat = x_hat_minus + K * (z(k) - H * x_hat_minus);
    P = (eye(2) - K * H) * P_minus;
    
    x_hat_hist(:,k) = x_hat;
end

% 绘图展示
figure;
subplot(2,1,1);
plot(1:N, x_true(1,:), 'b', 'DisplayName', 'True State');
hold on;
plot(1:N, x_hat_hist(1,:), 'r--', 'DisplayName', 'Estimated State');
legend;
xlabel('Time step');
ylabel('State value');
title('Estimation of State 1');

subplot(2,1,2);
plot(1:N, x_true(2,:), 'b', 'DisplayName', 'True State');
hold on;
plot(1:N, x_hat_hist(2,:), 'r--', 'DisplayName', 'Estimated State');
legend;
xlabel('Time step');
ylabel('State value');
title('Estimation of State 2');

代码分析

参数设置部分：
- dt 定义了时间步长，这在离散化系统中非常关键，它决定了每次迭代之间的时间间隔。
- A 是状态转移矩阵，描述了系统从一个时刻到下一个时刻状态的线性变化关系。这里 A = [1 dt; 0 1] 适用于简单的匀加速模型，第一行表示位置的更新与前一时刻位置和速度有关，第二行表示速度的更新只与前一时刻速度有关（假设无加速度噪声干扰）。
- H 观测矩阵用于将系统状态映射到观测空间。这里简单设置为 [1 0]，意味着我们只观测状态向量中的第一个元素（比如位置）。
- Q 和 R 分别是过程噪声协方差和观测噪声协方差。Q 描述了系统内部状态变化的不确定性，R 则描述了观测过程中引入的噪声大小。

初始化部分：
- x_hat 初始状态估计设为零向量，P 初始协方差估计设为单位矩阵。这是一种常见的初始设置，因为在没有任何先验信息时，我们假设初始状态为零且不确定性为单位矩阵所表示的均匀分布。

数据生成部分：
- 通过循环生成 N 个时间步的真实状态 x_true 和观测数据 z。真实状态通过状态转移矩阵 A 以及过程噪声 sqrtm(Q) randn(2,1) 得到更新。观测数据则是在真实状态基础上通过观测矩阵 H 并添加观测噪声 sqrt(R) randn 生成。

EKF 主体实现部分：
- 预测步骤：根据前一时刻的状态估计 xhat 和协方差估计 P，利用状态转移矩阵 A 预测当前时刻的状态 xhatminus 和协方差 Pminus。
- 计算卡尔曼增益：根据预测的协方差 Pminus、观测矩阵 H 和观测噪声协方差 R 计算卡尔曼增益 K。这个增益决定了观测数据对状态估计更新的权重。
- 更新步骤：利用卡尔曼增益 K、观测数据 z(k) 和预测状态 xhatminus 更新状态估计 xhat 和协方差 P。

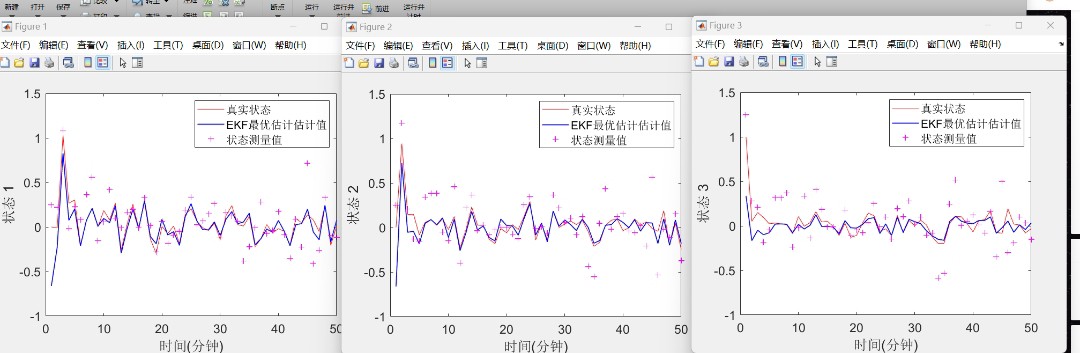
绘图部分：

最后通过Matlab的绘图函数，将真实状态和估计状态绘制在同一张图上，直观地展示EKF对系统状态的估计效果。

通过这样一个基于Matlab的EKF实现，我们可以有效地对非线性系统信号进行滤波和状态估计。希望这篇博文能帮助大家更好地理解和应用EKF。