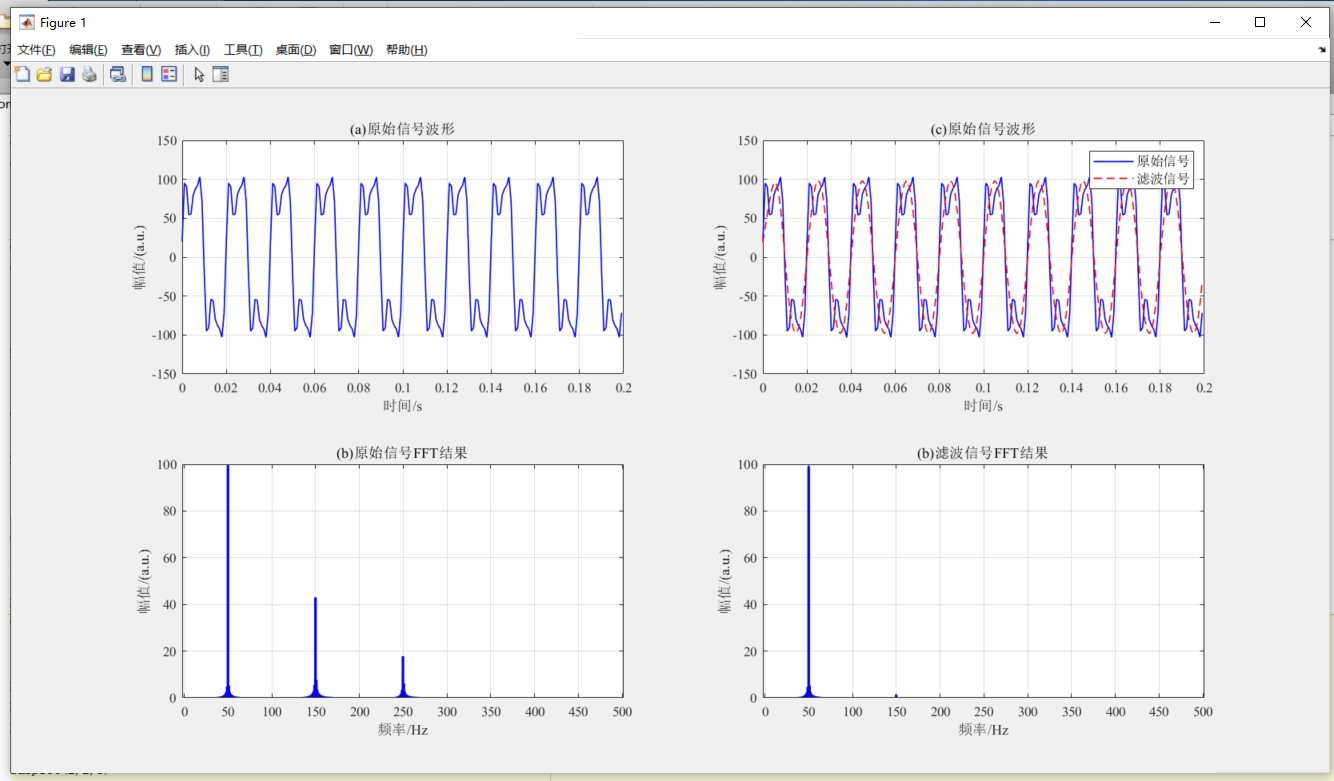
基于matlab的FFT频谱分析,数字滤波器。 可进行谐波提取,可实现对仿真模型中示波器的波形数据或者外部采样数据进行频谱分析和自定义频段清除,也可以对已有数据特定频段的数据进行提取。 滤波前后波形无相位滞后,幅值无衰减。 图a是原始信号,含三次,五次谐波,图b是原始信号频谱分析(FFT)结果,图c是滤除三次和五次谐波信号后的对比结果,图d是滤波后波形频谱分析(FFT分析)结果。
在信号处理领域,快速傅里叶变换(FFT)和数字滤波器是两大核心工具。本文将通过分析一个MATLAB实现案例,深入探讨如何利用这些技术进行信号频谱分析和滤波处理。
功能概述
该MATLAB代码包提供了完整的信号处理解决方案,主要包含两大功能模块:
- 合成信号分析模块 - 通过数学公式生成包含多个频率成分的测试信号
- 实测信号处理模块 - 处理外部采集的真实世界数据
两个模块都实现了完整的处理流程:信号生成/加载 → 时域分析 → FFT频谱分析 → 滤波器设计 → 滤波处理 → 结果可视化。
核心算法原理
信号合成与特征分析
在第一模块中,代码通过叠加不同频率的正弦波构建测试信号:
f1 = 50; % 基波频率 50Hz
f2 = 3*f1; % 3次谐波 150Hz
f3 = 5*f1; % 5次谐波 250Hz
Fs = 10*f3; % 采样频率(满足奈奎斯特准则)这种合成方法模拟了电力系统中常见的谐波污染情况,为后续的滤波器性能测试提供了理想的数据源。
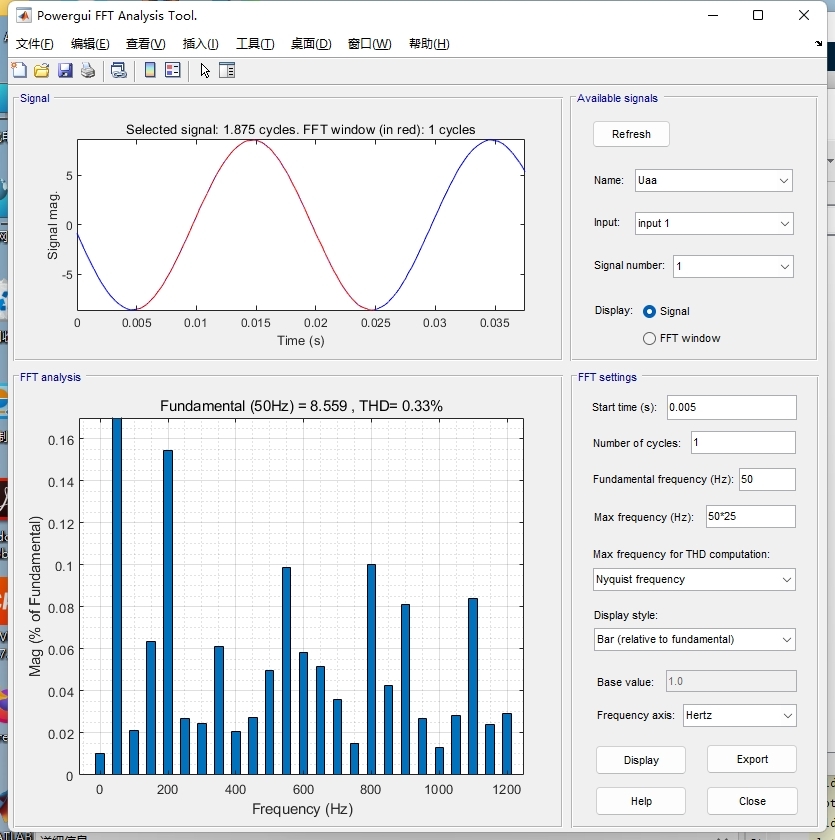
FFT频谱分析技术
代码采用了标准的单边频谱计算方法:
Y = fft(y1); % 执行FFT变换
L = length(y1);
P2 = abs(Y/L); % 计算双边谱
P1 = P2(1:L/2+1); % 提取单边谱
P1(2:end-1) = 2*P1(2:end-1); % 调整幅值(除直流分量外)
f = Fs*(0:(L/2))/L; % 构建频率轴这种处理确保了频谱幅值的物理意义正确,能够准确反映各频率成分的实际强度。
椭圆滤波器设计
代码选用椭圆滤波器实现频域滤波,其设计流程如下:
% 滤波器规格参数
fp = 60; % 通带截止频率
fs = 100; % 阻带起始频率
rp = 0.05; % 通带纹波
rs = 40; % 阻带衰减
% 滤波器设计
[N, wp] = ellipord(wp, ws, rp, rs); % 计算最小阶数
[B, A] = ellip(N, rp, rs, wp); % 设计滤波器系数
y3 = filtfilt(B, A, y1); % 零相位滤波椭圆滤波器的优势在于在给定性能指标下能够实现最低的滤波器阶数,同时filtfilt函数的使用消除了常规滤波引入的相位失真。
数据处理流程
模块一:合成信号处理
- 信号生成 - 创建包含50Hz基波、150Hz和250Hz谐波的复合信号
- 时域可视化 - 绘制原始信号波形,展示各频率成分的叠加效果
- 频谱分析 - 通过FFT揭示信号的频率组成,验证谐波存在
- 滤波处理 - 设计低通滤波器去除高频谐波成分
- 结果对比 - 从时域和频域两个维度展示滤波效果
模块二:实测信号分析
该模块面向实际应用场景,处理流程包括:
- 数据加载 - 从外部文件导入实测数据(如示波器采集的波形)
- 参数配置 - 根据实际采样情况设置Fs、Data_num等关键参数
- 自适应处理 - 相同的算法框架适配不同的数据特征
- 灵活滤波 - 根据实际需求调整滤波器截止频率
技术特色与优势
1. 完整的可视化分析
代码提供了4个子图的综合展示:
- 原始信号时域波形
- 原始信号频谱分析
- 滤波前后时域对比
- 滤波后频谱验证
这种多角度可视化使得用户可以直观理解信号处理全过程。
2. 工程实用性强
第二模块特别考虑了工程应用需求:
- 支持外部数据导入
- 参数可配置适应不同场景
- 处理真实世界信号的复杂性
3. 算法稳健性
- 采用零相位滤波技术避免信号失真
- 规范的频谱计算方法保证结果准确性
- 灵活的滤波器参数调整机制
应用场景
该技术方案在多个领域具有广泛应用价值:
- 电力系统谐波分析 - 检测电网中的谐波污染,评估电能质量
- 机械振动监测 - 分析旋转机械的振动特征,实现故障诊断
- 生物医学信号处理 - 提取心电、脑电等生理信号中的特征成分
- 通信信号处理 - 分离混合信号中的不同频率分量
总结
本文分析的MATLAB代码实现了一个专业级的信号处理系统,将FFT频谱分析与数字滤波技术有机结合。其核心价值在于提供了一套从理论到实践的完整解决方案,既可用于算法教学演示,也能满足工程实际应用需求。通过灵活的模块化设计,用户可以根据具体需求选择合成信号测试或实测数据处理,为各类信号分析任务提供了可靠的技术支撑。
该实现的优势在于其算法的严谨性、结果的可视化程度以及工程的实用性,体现了信号处理理论在实际应用中的强大能力。




















 488
488

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








