无人机移动性与通信计算联合优化

空地协同网络中无人机的移动性、通信与计算联合优化

Jianshan Zhou，田大新，IEEE高级会员，盛Zhengguo，IEEE高级会员，段旭婷，和沈学民，IEEE会士

摘要

无人机（UAV）在各类5G或超越5G（B5G）使能的 物联网（IoT）应用中发挥着重要作用。然而，无人机在空地协 同网络中的性能受到其移动性以及空对地通信和计算行为的显著 影响。本文研究了一种面向无人机的计算卸载系统，其中无人机 希望借助地面边缘计算基础设施（即路侧单元（RSU））完成 其机载计算需求。目标是最大化无人机的能量效率。具体而言， 本文建立了一个非凸约束最优控制问题，通过联合考虑无人机纵 向移动性、空对地通信和计算动态之间的耦合效应，优化无人机 的整体能效。为应对原始问题的耦合复杂性和非凸性，本文提出 一种原始分解方法，将该问题转化为一个凸子问题和一个主问题； 随后通过求解子问题推导出依赖于移动性信息的闭式最优传输功 率控制。将该闭式最优功率控制嵌入主问题后，提出一种基于梯 度投影的迭代算法，以获得纵向加速度控制与功率控制的联合最 优解，并从理论上证明了该算法的可行性与收敛性。大量仿真验 证了所提方法在约束满足和收敛速度方面的有效性，对比结果还 表明，该方法在全局能效方面优于其他基准方法。

一、引言

THE 无人机（UAV）与先进的信息与通信技术（I CT）的融合催生了从遥感监测到灾难救援等一系列广泛应 用[1],[2]。通常情况下，无人机可构成空中子网络，并 通过空对地（A2G）通信协助地面网络（例如车联网）， 从而推动了一种被称为“空地协同网络”或“空地一体化 网络”的新型网络架构的发展[3]。在设想的超越5G（ B5G）或第六代移动网络（6G）中，无人机也被视为与低 地球轨道（LEO）和地球静止轨道（GEO）卫星系统协同 的关键角色，从而构建天地空一体化网络（SAGIN） [4],[5]。该架构能够实现无缝且灵活的通信覆盖、信息服 务以及城市计算等众多新兴物联网（IoT）应用。

此外，移动边缘计算（MEC）目前被视为一种新兴 范式，可在B5G/6G中支持低延迟关键和计算密集型应用， 能够在网络边缘为资源需求高的移动用户提供靠近边缘的 计算资源[6]–[9]。因此，许多研究人员致力于设计支持 MEC的通信与网络系统的新颖协作架构、协议和算法， 例如低延迟雾无线接入网络架构[10],、协同雾计算方法 [11],以及用户的协同通信与计算方法[12]。这些传统研 究主要关注地面移动场景中的通信与计算优化设计。在 B5G/6G的愿景中，无人机也可配备计算和存储资源，从 而作为飞行MEC节点为物联网应用提供按需通信与计算 支持。因此，研究无人机与地面基础设施在通信和计算方 面的空地协同至关重要。

尽管无人机提供了许多潜在的诱人机遇，但在空地协 同网络和天地一体化网络的实际应用中仍存在一些亟待解 决的重大挑战，例如

由于高移动性导致的无线链路动态特性，以及通信和计算 资源的限制，使得系统设计更加复杂。更重要的是，在支 持移动边缘计算的空地协同网络中，无人机的移动性、计 算卸载和通信功率控制本质上是相互耦合的。能耗是与无 人机移动性、通信和计算最相关的因素之一。如果没有适 当的联合优化设计，无人机所携带的有限能源资源既无法 高效支持自身收集和处理计算任务，也无法延长其服务寿 命。因此，从联合优化设计的角度提升无人机的整体能量 效率具有重要意义，同时还需要在能源资源受限的飞行平 台上保持系统可靠性，以支持各种应用的处理。

A. 动机

无人机可与移动边缘计算技术相结合，以优化其机载资 源。在学术界和工业界，目前已有大量研究致力于开发面向 无人机辅助的移动边缘计算系统的高效节能系统[13]–[33]。

具体而言，在诸如[15]–[17],[19],[27],等许多研究中，无人 机被用作移动云节点，通过共享其机载计算资源为地面终端 用户提供服务。在上述工作中，无人机被视为移动边缘计算 场景中的服务提供者。然而，由于尺寸和负载限制，飞行中 的无人机所携带的能量资源相当有限，其运行寿命也高度依 赖于资源利用效率。因此，必须对无人机搭载的云节点进行 合理设计，以确保系统的实用性。此外，无人机自身也可能 存在密集型计算需求，尤其是在作为空域传感器用于采集和 处理大量感知数据（如航拍图像和视频流）时。因此，作为 物联网节点的无人机，面临着机载应用对海量存储和计算能 力的需求所带来的挑战。在这种情况下，无人机是资源渴求 型服务请求者，而非资源丰富型服务提供者。

受无人机灵活移动性和低成本商业化发展的启发，许 多研究人员也致力于为各种无人机辅助通信系统开发新型 的部署与移动性解决方案[34]–[36]。例如，Chouetal.提 出了一种面向搭载小基站的无人机群的能量感知三维部署 算法[34]。在[35],中，设计了一种智能反射面（IRS）优 化模型，以提升空地通信网络的平均信号干扰噪声比（ SINR），同时缓解小区间干扰。在[36],中，Chenet al.通过结合分布式能量最小化、灰色预测和动态生成树算 法，提出了一种统一共识模型，以实现大规模无人机群的 鲁棒部署。上述工作主要聚焦于面向无人机的部署与移动 性优化，而空地通信、计算调度与无人机移动性的联合优 化问题仍有待深入探索。

具体而言，无人机不仅需要适当地调度其计算需求的 卸载，还需要在一定的控制约束集下自主调整其运动。 无人机的整体能效性能本质上依赖于移动性、通信和计算 之间复杂的耦合效应，这对优化设计提出了重要挑战。一 方面，无人机与路侧单元（RSU）之间的成功卸载率依赖 于空对地通信的性能，同时无人机的计算任务分配还需考 虑其本地计算能力；另一方面，无人机的运动会影响其与 路侧单元之间的时变相对距离，从而进一步影响空对地通 信的动态特性。无人机的移动性、通信和计算占据了其大 部分能耗，因此应从全局角度进行最优控制。因此，本文 研究了无人机与地面基础设施如何以协作方式处理计算需 求，并提出了一种基于联合优化的新型面向无人机的节能 系统。在所考虑的场景中，飞行中的无人机能够通过空对 地通信自适应且动态地将全部或部分计算需求卸载至地面 边缘计算提供商（即路侧单元），以优化其有限能源资源 的利用效率。同时，无人机还需完成其飞行任务，如目标 跟踪和地面交通检测，即满足一系列移动控制约束。

B. 主要贡献

为此，我们研究了空地协同网络场景，并提出了一种 针对无人机的联合移动性、通信与计算优化方法，以最大 化其整体能量效率。具体而言，我们分别对无人机的纵向 运动、无线空对地通信以及本地计算建立了不同的模型。 基于最优控制理论的角度，我们进一步构建了一个联合最 优控制模型，该模型充分考虑了无人机移动性、通信和计 算之间的耦合动力学。将传输功率和纵向加速度作为无人 机的时变且受约束的决策变量。为应对最优控制系统中的 挑战，我们提出一种原始分解方法，将原问题转化为一个 子问题和一个主问题，从而降低复杂度，便于算法设计。 通过求解子问题，理论上推导出一种依赖于移动性信息的 闭式最优功率控制。随后，结合该最优功率控制，提出一 种基于梯度投影的算法来求解主问题，最终得到有限时域 上的联合最优控制解。据我们所知，本工作首次在空地协 同网络中实现了对无人机移动性、通信与计算的联合最优 控制，可为空地协同计算和跨层系统优化提供有意义的指 导。

关于建模与优化设计，我们工作的主要贡献有两方面： 我们通过考虑无人机纵向移动性、空对地通信和本地计 算的耦合动力学，建立了一个联合最优控制模型，然后 将这样一个复杂的约束优化模型分解为一个可处理的模型。 我们从理论上推导并验证了一种针对无人机最优传输功 率控制的闭式且依赖于移动性的表达式，该表达式用于 根据无人机的运动状态和外部应用需求动态调整计算卸 载。 基于最优功率控制的闭式表达式，我们进一步提出了一 种基于梯度投影的算法来求解联合最优控制模型。通过 理论分析，证明了所提算法在闭合控制约束域内的下降 可行性与收敛性。 我们进行了大量的仿真实验，以验证所提出方法的有效 性并展示其优势。我们将该方法与基于激进移动性、激 进卸载和本地计算机制的传统方法分别进行比较，结果 表明，在全局能效方面，我们的方法优于传统方法。

本文的其余部分组织如下：在第二节中回顾相关工作， 在第三节中建立联合最优控制的系统模型。在第四节中， 提出原始分解以进行模型转换，并推导出子问题的闭式解。 在第五节中，提出一种基于梯度投影的算法，并结合闭式 解对其收敛性进行理论分析。第六节进行性能评估，第七 节总结本文并展望未来工作。

II. 相关工作

由于具有高度的灵活移动性，无人机目前在各个领域 中发挥着重要作用。因此，基于无人机的多样化智能系统 正受到学术界和工业界的广泛关注。特别是，配备新兴信 息通信技术（ICT）和控制技术的无人机有望推动通信与 网络范式从传统的地面基础设施模式向空地协同范式转变 [1],[2],[5],[9]。例如，[3]提出了一种空地协同车联网的 新架构，其中利用多架无人机协助转发车辆信息并增强车 辆连接性。[13]通过集成无人机的中继功能，构建了一 种抗干扰的车载自组织网络。

具体而言，目前有许多研究人员专注于基于无人机的 网络系统的通信与轨迹联合优化设计。在[28],中，研究 人员建立了一个系统吞吐量最大化模型，以优化中继无人 机的传输功率及其飞行轨迹，并提出了基于逐次凸优化技 术的迭代算法。在[26],中，研究人员同样旨在最大化基 于无人机的车载通信系统的总数据速率，其中无人机作为 空中基站，并借助强化学习理论设计了轨迹控制方案。在 [24],中，也采用强化学习理论来设计无人机的轨迹，以 实现期望吞吐量最大化的目标 无人机辅助蜂窝网络的上行链路总速率。文献[20]利用深 度强化学习进行无人机能效控制设计，旨在提升基于无人 机的蜂窝通信系统的覆盖与连接性。在[29],[30],中，还 分别从能量效率角度研究了多架无人机的覆盖与部署优化 问题，应用了最优传输和块坐标下降法。在[14],[23],中， 作者研究了能效型无人机通信与轨迹优化问题，在其系统 设计中，以能量效率意义上的通信吞吐量作为优化目标。 不同的是，[14]采用序列凸优化技术求解其联合优化模 型，而[23]则基于交替方向乘子法（ADMM）提出了一 种迭代算法。除了关注通信与轨迹的联合设计外，许多研 究人员还致力于开发面向无人机的安全通信方法，通过联 合考虑无人机通信与移动性控制，如[25],[31]所示。从上 述研究[14],[20],[23]–[26],[28]–[31],可以看出，已有大量 重要且新颖的范式从联合无人机通信与移动性优化的角度 被设计并得到充分验证。然而，这些工作忽略了空地协同 场景中移动边缘计算的决策建模与优化，而计算相关能耗 实际上会影响无人机的整体能量效率。

由于移动边缘计算（MEC）被广泛认为是应对智能 但资源受限的移动设备上运行的计算/数据密集型应用挑 战的一项有前景的技术，已有大量研究致力于将MEC与 基于无人机的系统相结合。例如，[27]旨在最大化由无人 机支持的无线供能MEC系统的计算速率，提出了一种用 于地面终端用户计算卸载的两阶段和三阶段算法。在这种 情况下，以匀速运动的无人机作为计算资源提供者为地面 终端用户提供服务。在[4],中，无人机预计将与地面和空 间网络系统集成，形成天地一体化网络，并针对无人机边 缘服务器提出了一种联合资源分配与任务调度方法。在这 些场景中，为了降低建模复杂度，忽略了无人机的移动性 影响。此外，其他一些工作如[15]– [19],[21],[22],[32],[33]通过引入联合计算卸载与轨迹优化 的概念，使其研究区别于上述工作。具体而言，在[15], 中，无人机充当云节点，并利用连续凸逼近方法联合优化 其轨迹和比特分配，以支持来自地面移动终端用户的计算 卸载。然而，其系统设计的目标是最小化所有地面终端用 户的总能耗，而非无人机自身的能量消耗。类似地，在 [16],中，作者研究了地面用户的计算卸载与无人机服务 器轨迹设计的联合问题，并提出了一种基于对偶分解的惩 罚算法来处理系统模型的非凸性。优化目标是最小化

所有地面终端用户的最大延迟之和。在[18],中，作者旨 在通过联合考虑地面终端用户的计算卸载、无人机的轨迹 调度和资源分配，优化地面终端用户和无人机的平均加权 能耗。在他们的研究中，提出了一种基于李雅普诺夫的排 队分析和基于分解的算法设计的随机解。在[19],中，采 用了一种基于连续凸近似算法来最小化无人机的能耗，其 中联合考虑并优化了终端CPU频率、卸载数据量、地面终 端用户的发射功率以及无人机的飞行轨迹。尽管[19]的系 统模型已考虑了计算和与移动相关的能耗，但并未对传输 功率进行控制或优化，并且将无人机的初始或终端位置和 速度视为自由设计变量，以降低其轨迹优化的复杂度。实 际上，无人机的初始或终端状态通常受到限制，即期望无 人机以指定的初始位置和给定的速度起飞，并最终到达目 标状态，同时优化其飞行轨迹，尤其是在被赋予特定飞行 任务的情况下。在[21],中，也采用了结合丁克尔巴赫分数 规划算法的连续凸逼近方法，用于处理联合优化无人机轨 迹、地面用户发射功率和计算负载分配的问题。在[22], 中，仅将无人机的轨迹作为设计因素，并构建了一个混合 整数非凸模型以最大化由无人机服务的边缘用户的总速率。 在[33],中，作者联合优化了带宽分配、计算资源和无人 机的飞行轨迹。研究人员提出了一种三步优化方案以应对 建模复杂度[22],，其中第一步固定无人机的轨迹和分配 的带宽以调度计算资源，第二步在固定已获得的计算资源 分配的基础上优化带宽分配，最后一步设计无人机的轨迹。 然而，由于原始模型中的内在耦合效应未被充分纳入设计 步骤，因此通过该三步设计方案获得的整体解可能在全局 最优性方面并非最优。除了上述工作外，基于连续凸近似 的各种方法还被广泛应用于解决联合飞行轨迹与无线缓存 优化问题，例如可参见[17],[32]。然而，即使连续凸逼近 技术在处理建模非凸性方面具有较强能力，但由于近似与 实际的目标或约束方程之间可能存在差距，在迭代过程中 仍可能无法满足解的可行性。

本文通过联合建模无人机的纵向移动性、空对地无线 通信和机载计算，并基于原始分解和梯度投影机制提出一 种新颖的联合优化设计，将本研究的贡献与上述工作区分 开来。具体而言，与上述工作不同，我们将无人机视为资 源需求者而非资源丰富的服务器，且无人机的纵向加速度 和传输功率均为设计变量。在本文中，无人机的轨迹并非 直接进行优化，而是通过由无人机运动学驱动的

最优加速度控制信号。我们的模型还考虑了初始和终端约 束。此外，明确处理了无人机移动性、通信与计算之间的 耦合效应，并且能够推导出一种闭式且依赖于移动性信息 的最优功率控制。基于该闭式功率控制，我们进一步提出 了一种梯度投影法来求解主问题，其迭代可行性与收敛性 在理论上得到了证明并具有良好的保障。

III. 系统模型

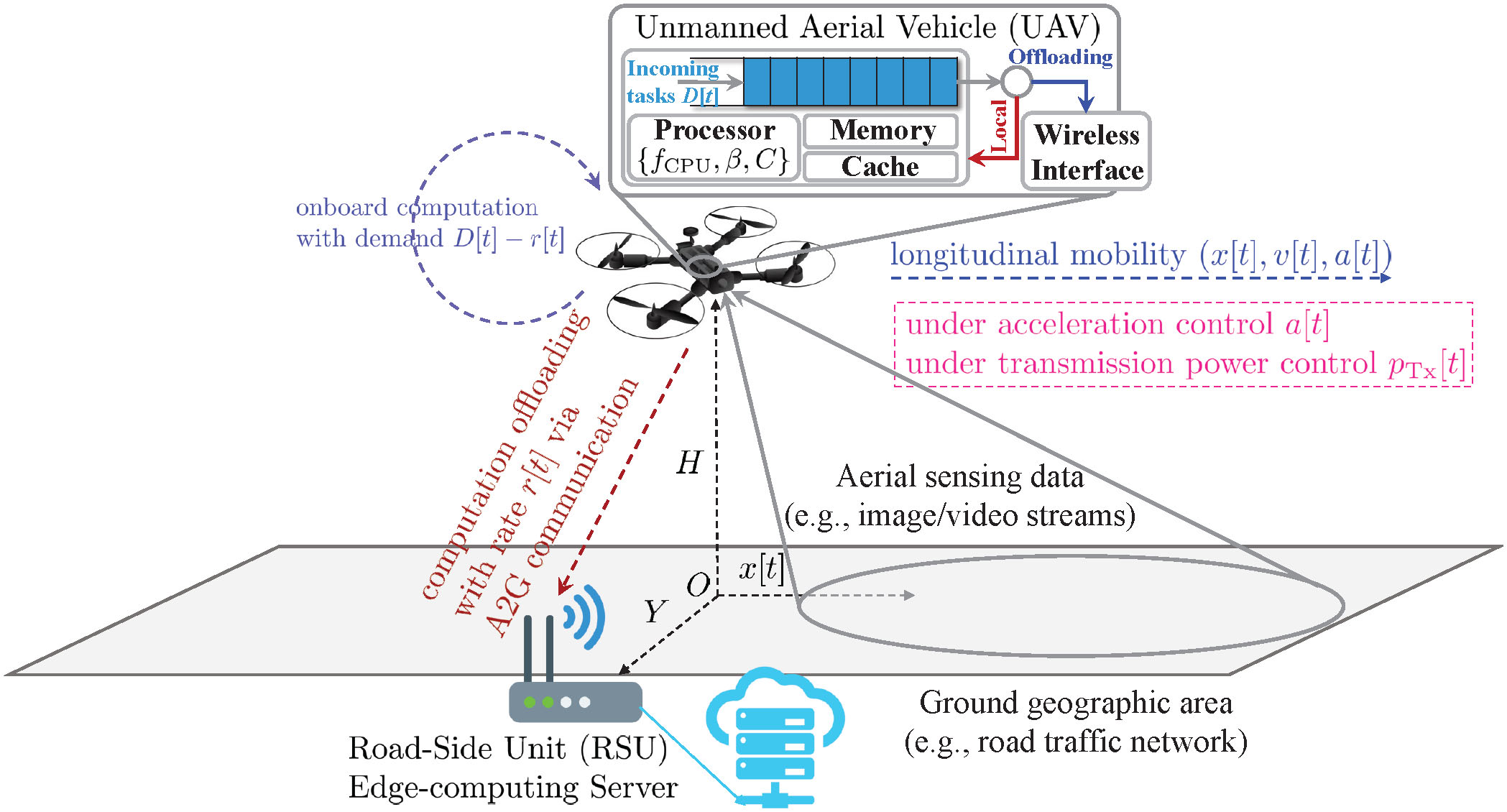
如图1所示，我们考虑一种通用的空对地计算卸载场 景，其中具有有限通信、计算和移动性能力的无人机需要 将其部分或全部计算任务卸载至地面基础设施（例如，路 侧单元）进行远程执行。在这种情况下，无人机需要在适 当的速度控制策略下，从给定的初始位置飞行到目标位置。 从系统角度而言，无人机的移动性将显著影响其与路侧单 元之间相对地理距离随时间的变化动态，从而进一步影响 空对地通信链路的性能。另一方面，依赖于空对地链路传 输的计算卸载也会受到无人机移动性的影响。此时，无人 机的移动性、通信和计算动态本质上是耦合的，因此我们 旨在建立一个联合优化框架。为便于实际实现，我们假设

连续时间范围[t0, t f]被离散化为 N个离散区间，每个区间 的持续时间为Δτ=（t f − t0）/N秒，即[t0, t f]=[t0, t1) ∪[t1, t2) ∪··· ∪[tN−1, tN]，其中 t0 ≥ 0和 t f > t0分别表 示初始时刻和终止时刻。令 t为时间间隔索引，满足 t= 0, 1,…, N。在接下来的子章节中，我们将针对无人机的移 动性、通信和计算分别建立不同的模型。

A. 移动性建模

为简化问题且不失一般性，我们考虑优化目标无人机的纵 向移动性，

假设在[t0, tf]内飞行高度和横向位置保持不变。然而，此 处需要指出的是，本文中的移动性建模方法可以很容易地 扩展到多维，例如三维坐标空间。设无人机的飞行高度和 横向位置分别为 H> 0和 Y> 0，而时变的纵向位置表示 为 x[t]。此外，纵向速度表示为 v[t]。利用这些符号，我 们可以将无人机的时变移动状态表示为一个列向量s [t]=[x[t], v[t]]T。同时，令时变速度控制为 a[t]。接下来， 我们进一步提出采用时间离散双积分模型的动力系统来描 述无人机的移动性，如下所示

s[t+ 1]= As[t]+ Ba[t], ∀t, (1)

其中A和B分别为状态矩阵和控制矩阵，其定义如下

A [1 Δτ 0 1], B [21(Δτ)2 Δτ]. (2)

为了对无人机的与移动相关的能耗进行建模，我们假 设该无人机为广泛存在于现有文献中的旋翼类型。令 Emob[t]表示其在 t时的推进能量消耗。根据[14],[15], [37]， Emob[t]可被近似建模为

Emob[t]= a1 ‖v[t]‖3+ a2 ‖v[t]‖(1+ ‖a[t]‖2 g2), (3)

其中，a1> 0和 a2> 0是与旋翼无人机的流体动力学和气 动布局相关的两个正系数。 g为恒定的重力加速度，其典 型值为9.8m/s2。

B. 通信建模

设无人机位置为pUAV[t]=[x[t], Y, H]T，特定路侧单元 为pRSU。无人机与路侧单元之间的相对距离可表示如下

d[t]= ‖pUAV[t] − pRSU‖, ∀t. (4)

为了对空对地链路（A2Glink）上的物理层传输进行建 模，我们采用近年来研究中广泛使用的香农形式（ Shannon’sform）数据速率公式[13]–[19],[30]。设分配 给该空对地链路的可用带宽为 ω，该链路上的路径损耗指数 为 α，平均噪声功率为N0，无人机在 t处的传输功率为 pTx[t]。 当采用功率控制pTx[t]时，无人机在 t处的通信能耗为

E Tx[t]= pTx[t]Δτ. (5)

此外， t处空对地链路的可实现数据速率被建模为传 输功率pTx[t]和相对距离 d[t]的对数函数，如下所示

r[t]= ω log2(1+ a 3pTx[t]d − α [t]), (6)

其中a3 = a 4 /N 0 和 a4 > 0 是用于表征空对地链路衰减的附加 标量因子。当空对地链路为视距链路时，a 4 可固定为 a 4 = 1。 当链路为非视距（NLoS）时， a4 ∈(0,1)。此外，一些现有 研究[30],[38],[39]还建议a4可被定义为随机情况下的空对 地链路平均衰减，即a4= pLoS+ ηpNLoS，其中 pLoS和 pNLoS 分别表示视距（LoS）和非视距（NLoS）情况的概率， η表 示由于非视距（NLoS）效应引起的衰减因子。

C. 计算建模

关于无人机的计算卸载，我们用 t时刻到达的以比 特为单位的计算需求 D[t]来表示，这是空‐地一体化边缘 计算网络中的外生因素。给定卸载数据速率，即公式(6) 中的 r[t]，无人机需要消耗一定的机载能量来处理部分数 据 q[t]= D[t] − r[t]Δτ。具体而言，设机载CPU的有效切 换电容为 β，机载CPU的时钟频率为 fCPU，处理每比特 输入数据所需的CPU时钟周期数为 C，则可将处理 q[t]比 特输入数据的计算能耗建模如下

Ecom[t]= βCq[t]f2 CPU= βC(D[t] − r[t]Δτ) f2 CPU. (7)

D. 联合优化模型

利用上述建立的移动性、通信和计算模型，我们可以 在一组状态和控制边界约束下进一步提出联合优化模型。 具体而言，设初始状态为s0=[x0, v0]T，其中 x0为初始纵 向位置， v0为初始纵向速度。进一步记无人机运动过程 中纵向位置的上界为xf> x0。因此，假设纵向位置边界 为 X [x0, xf],，而纵向速度边界为 V [vmin, vmax]， 其中 vmin和 vmax分别为无人机纵向速度的上界和下界。 于是，我们可以将状态边界约束表示为s[t] ∈S X × V， 其中 t= 0, 1,…, N −1。在终止时刻 t= N，记终端状态 空间为 Sf，即令 s[N] ∈Sf。此外，设允许的最小和最大 速度控制分别为amin和 amax，允许的最小和最大功率控 制分别为pmin和 pmax。在 t时刻的联合系统控制可表示为 u[t]=[a[t],pTx[t]] T。

因此，我们将无人机通信、计算和移动性所需总能耗 的联合最小化全局目标表述为

J(s[0]; u[0],…, u[N −1]) = g(s[N], N)+ N−1 ∑ t=0 g(s[t], u[t], t), (8)

其中 g(s[t], u[t], t)是系统在状态s[t]下、控制量u[t]在 t时刻的成本函 数，该函数综合了与无人机移动性、通信和计算能力相关的能耗， 即

g(s[t], u[t], t)= E mob[t]+ E Tx[t]+ E com[t], (9)

而 g(s[N], N)是取决于无人机实际到达的终端状态s[N]的终端成本。

为了建模该终端成本函数，我们可以将s f =[x f , v f ] T ∈S f 设定期望 值

无人机在 t= N处的终端状态，其中 vf表示期望的终端 速度。基于此，我们提出 g(s[N], N)的效用函数如下

g(s[N], N)= ⎧⎨⎩a1 ∥∥∥[xf−x[N] Δτ , vf − v[N]]∥∥∥ 3 , s[N] ∈Sf; Cpenalty, otherwise; (10)

其中a1如(3)式所示， Cpenalty是当无人机在结束时无法达 到期望的终端状态sf时的一个足够大的惩罚因子。由(9)式可 知，0 ≤ g(s[N], N)≤ Cpenalty。当s[N]= sf时，终端成本g(s [N], N)为零；而当s[N]偏离sf时，终端成本 g(s[N], N)为正 值。终端状态s[N]越接近sf，终端成本 g(s[N], N)越小。

为了优化整体能量效率，我们进一步提出了以下联合 优化模型 M1，将 a[t]和pTx[t]作为控制变量。

min {u[t],t=0,…,N−1} : J(s[0]; u[0],…, u[N −1]) s.t. ⎧⎪⎪⎨⎪⎪⎩ s[t+ 1]= As[t]+ Ba[t], t= 0,…, N −1; s[0]= s0; s[t] ∈S, t= 0,…, N −1; a[t] ∈[vmin, vmax], t= 0,…, N −1; pTx[t] ∈[pmin,pmax], t= 0,…, N −1. (11)

从(11)可以看出，M1是在一组边界约束下的复杂动 态最优控制问题。实际上，使用诸如牛顿法等传统优化算 法直接求解M1是困难甚至不可能的。在接下来的章节中， 我们希望通过结合原始分解方法和基于梯度投影的方法， 提出一种求解M1的新方法。

IV. 基于凸优化的原始分解方法

在原始模型M1中，我们发现速度控制a[t]通过距离 相关的传输数据速率（即如(6)式所示的 r[t]）与通信能耗 Ecom[t]在发射功率控制pTx[t]方面直接耦合。这促使我们 提出一种原始分解变换，将M1转化为另一种数学上易于 处理的等效形式。

A. 原始分解

具体而言，在每个 t处，我们固定无人机与路侧单元之 间的距离 d[t]，该距离取决于当前系统状态s[t]，因此可以独 立地对目标函数关于pTx[t]进行优化。此时，基于(5)、(6)和 (7)，在 t处给定固定的 d[t]，我们构建了以下模型M2

h(d[t])= min p Tx [ t ] : pTx[t]Δτ+ βC(D[t] − r[t]Δτ)f 2 CPU s.t.{ r[t]= ω log2(1+ a 3pTx[t]d − α [t]) pTx[t] ∈[pmin ,pmax], (12)

其中 h(d[t])表示M2的最优值。

根据M2，原始模型M1 随后被重新表述如下，该模型记 为 M3。

min {a[t],t=0,…,N−1} : g(s[N], N)+ N−1 ∑ t=0 [Emob[t]+ h(d[t])] s.t. ⎧⎪⎨⎪⎩s[t+ 1]= As[t]+ Ba[t], t= 0,…, N −1; s[0]= s0; s[t] ∈S, t= 0,…, N −1; a[t] ∈[vmin, vmax], t= 0,…, N −1. (13)

如上所述，利用分解结构，我们可以针对单一决策变量 pTx[t]求解子问题M2，然后再进一步求解关于 a[t]的原问 题。子问题M2和原问题M3实际上共享了包含在 d[t]中的 共同信息。

B. 子问题 M2 的凸优化

为了处理 M2，我们首先通过证明其凸性来推导以下结果。

推论1: 子问题M2 保证在[pmin,pmax]中仅存在一个唯一的全局最 优解。

证明： 为简便起见，我们将 M2的目标函数表示为 F (pTx[t])= pTx[t]Δτ+ βC(D[t] − r[t]Δτ)f2 CPU。 F(pTx[t]) 关于F(pTx[t])的二阶导数表示为

d2F(pTx[t]) d(pTx[t])2 = βCf2 CPUΔτωa2 3 d−2α[t] ln2(1+ a3pTx[t]d−α[t])2 . (14)

回顾 d[t]> 0，我们可以得到d 2F(pTx[t]) d(pTx[t])2 > 0。结 果表明， F(pTx[t])关于pTx[t]是一个严格凸函数。此外， M2 被闭区间[pmin,pmax]所约束。因此，这很好地保证 了严格凸性，从而证明了该推论。

根据推论1，我们定义与M2相关的拉格朗日函数如下

L(pTx[t], λ1, λ2)= F(pTx[t])− λ1(pTx[t] −pmin) − λ2(pmax −pTx[t]), (15)

其中λ1 ≥ 0和 λ2 ≥ 0是两个非负的拉格朗日乘子。根据 一阶必要条件（即卡鲁什‐库恩‐塔克（KKT）条件），我 们得到以下结果：

推论2: 对于M2，假设 p opt Tx[t]是其唯一的全局最优 解。如果 pmin< p o p t Tx[t]< pmax，则拉格朗日乘子λ1和 λ2可以同时等于零；否则，若 p o p t Tx[t]= pmin，我们仅 有 λ2= 0，且若 p o p t Tx[t]= pmax，则有 λ1= 0。

证明： 根据推论1，子问题M2保证存在唯一的全局 点 p o p t Tx[t]。它满足如下KKT条件 ⎧⎪⎨⎪⎩ ∇L(p o p t Tx[t], λ1 , λ2) = ∇F(p o p t Tx[t])− λ 1 + λ 2 = 0; λ 1(p o p t Tx[t] −pmin) = 0; λ 2(pmax −p o p t Tx[t])= 0; λ 1 ≥ 0, λ 2 ≥ 0, p o p t Tx[t] ∈[pmin ,pmax]. (16)

在(16)中，当最优解点为内点，即p o p t Tx [t] ∈(pmin ,pmax) 时，互补松弛性（即

第二个和第三个方程以及拉格朗日乘子的非负性导致 λ1= λ2= 0。否则，当popt Tx[t]= pmin时，第三个互补松 弛性导致λ2= 0；而当 popt Tx[t]= pmax时，第二个互补松 弛性导致 λ1= 0。

由推论2可知，当M2的最优解点是[pmin,pmax]的边 界点时，这两个拉格朗日乘子 λ1和 λ2不能同时为正。即 始终成立λ1 × λ2= 0。基于推论2，我们推导出M2的闭 式最优解，如下述定理所示。

定理1： 对于 M2，定义 p∗ Tx[t]、 λ∗ 1和 λ∗ 2如下 ⎧⎪⎨⎪⎩p∗ Tx[t]= βCf2 CPUω ln2 − 1 a3 d−α[t]; λ∗ 1= Δτ − βCf2 CPUΔτωa3 d −α[t] ln2(1+a3pmind −α[t]); λ∗ 2= βCf2 CPUΔτωa3 d −α[t] ln2(1+a3pmaxd −α[t]) −Δτ. (17)

M2、 popt Tx[t]的最优解以及拉格朗日乘子 λ1和 λ2必须 满足以下三种情况之一：

i) 如果pmin ≤ p∗ Tx[t] ≤ pmax，最优解为 p opt Tx[t]=p∗ Tx[t]。 拉格朗日乘子满足 λ1= λ2= 0。

ii) 如果λ∗ 1> 0，最优解为 p opt Tx[t]= pmin，且拉格朗日乘子 分别为λ1= λ∗ 1 和 λ2= 0。

iii) 如果λ∗ 2> 0，最优解为 p opt Tx[t]= pmax，且拉格朗日 乘子分别为λ1= 0 和 λ2= λ∗ 2。

证明： 根据推论2，λ1和 λ2的值仅可能有三种情况， 即(i) λ1= λ2= 0，(ii)λ1> λ2= 0，以及(iii) 0= λ1< λ2。 在第一种情况下，我们可以求解(16)中的梯度条件，即 Δτ − βCf 2 CPUΔτωa3 d −α[t] ln2(1+ a3pTx[t]d−α[t]) − λ1+ λ2= 0, (1
续上：

18) 使用 λ1= λ2= 0，结果如(17)中的 p ∗ Tx[t]。因此，最优解为 p opt Tx[t]= p ∗ Tx[t]（当 p ∗ Tx[t] ∈[pmin,pmax]时）。

在第二种情况下，λ1> 0表明最优解必须是 p o p t Tx[t]= pmin。 结合该结果与λ2= 0，我们可以从梯度条件中求解 λ1，即 Δτ − βCf 2 CPU Δτωa3 d −α[t] ln2(1+ a3pmind −α[t]) − λ1= 0, (19) 这导致如(17)中的 λ ∗ 1 。因此，如果 λ ∗ 1 > 0，我们可以设置 λ 1 = λ ∗ 1 。

按照相同的逻辑，在第三种情况下，λ 2 > 0表明最优解必须是 p o p t Tx[t]= pmax。利用λ 1 = 0，我们还可以从梯度条件推导出 λ 2 ，即 Δτ − βCf 2 CPU Δτωa3 d − α [t] ln2(1+ a3pmax d− α [t]) + λ2= 0, (20) 这导致 λ ∗ 2 如(17)所示。因此，如果λ ∗ 2 > 0，我们可以设置 λ 2 = λ ∗ 2 。

回想一下，M2 保证了严格凸性。它只有一个唯一的最优解 点，且必须满足上述三种情况之一。此时，该定理得证。

根据定理1，我们可以进一步推导出最优目标函数 h( d[t])在以下三种情况下的闭式表达式：

表I 符号列表

i) 当 pmin ≤ p ∗ Tx[t] ≤ pmax成立时，通信与计算的最优能耗 为 h(d[t])=(βCf 2 CPUω ln2 − 1 a3 d −α[t]) Δτ+ βCf 2 CPUD[t] − βCf 2 a3 d −α[t]βCf 2 CPUω ln2 )Δτ. (21) ii) 当 λ ∗ 1> 0成立时，通信和计算的最优能耗为 h(d[t])= pminΔτ+ βCf 2 CPU D[t] − βCf 2 CPU ω log2(1+ a3pmind −α [t])Δτ. (22) ii) 当λ ∗ 2 > 0成立时，通信与计算的最优能耗为 h(d[t])= pmax Δτ+ βCf 2 CPU D[t] − βCf 2 CPU ω log2(1+ a3pmax d −α [t])Δτ.(23)

为了验证上述所提定理，我们进行了大量实验，并将 闭式模型获得的理论结果与基于数值解的结果进行比较。 具体而言，仿真中一架无人机在道路交通网络上空巡航， 需要通过其自身与路侧单元之间的空地协作，按需处理其 收集的计算任务（例如，实时交通感知数据），如图1所 示。根据现有文献[14],[15],[37],[40],，与移动性相关的仿 真参数

表II 仿真参数

无人机的通信与计算模型如表II所示。此外，我们将无人 机的飞行高度和纬度分别固定在50米和10米，而路侧单元 的海拔和纬度位置设为零。路侧单元的纵向位置设置为 x 0 +x f 2 ，即位于无人机轨迹的中间位置。无人机的初始速度 和终端速度设为v0= v f = 1米/秒，飞行持续时间设为 t f − t0= 30秒，所有 t的计算需求固定为 D[t]= 2 × 106比 特。需要注意的是，由于此处未对无人机的移动性进行联 合优化，因此设定无人机以恒定速度移动。联合优化方法 将在性能评估部分进行验证。

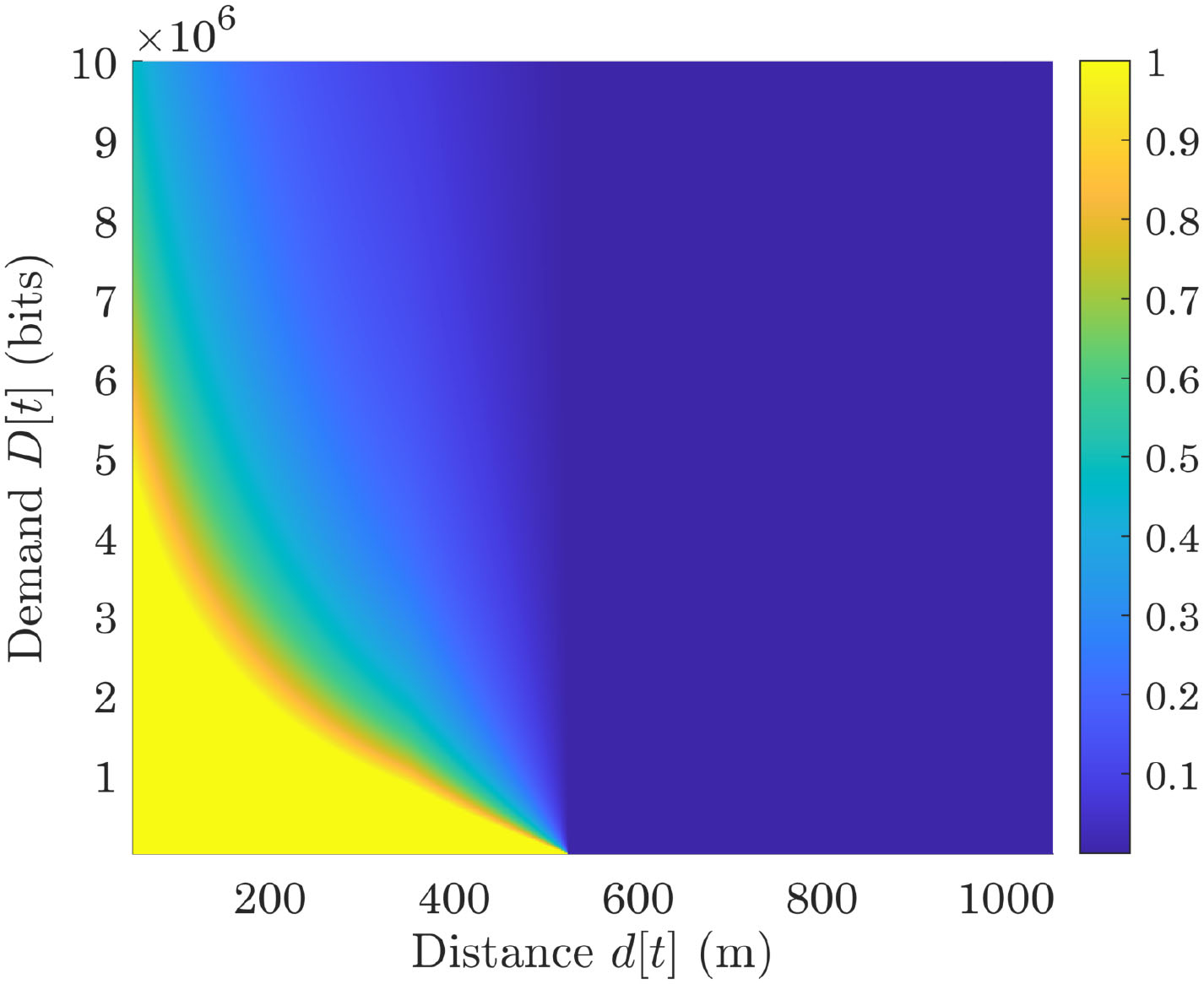
我们计算了无人机与路侧单元之间相对距离变化时的 最优传输功率， d[t]。结果如图2所示。图3还展示了卸载 与本地计算中的最优能耗。

随着 d[t]的变化。从图2可以看出，当相对距离 d[t]低于 约200米时，无人机可以将其传输功率增加到最大水平， 以提高卸载率，并从远程计算中获得更好的收益。当 d[t] 大于约500米且无人机正在远离路侧单元（RSU），即 d[t]增大时，无人机将其传输功率降低至最低水平，并主 要通过本地计算处理计算需求。这意味着当相对距离变大 时，无人机无法从计算卸载中获得显著收益，因此预期采 用本地计算而非远程计算。图3显示，增加相对距离将增 加机载通信与计算的整体能量消耗。此外，从两个图中可 以看出，闭式解结果与数值解相同，验证了所提定理。在 图4中，我们评估了在不同情况下待卸载数据量与总计算 需求之间的最优卸载比率。图4还表明，当无人机远离路 侧单元（RSU）时，会通过降低传输功率来减少卸载的数 据量，且最优卸载比率随总计算需求的增加而减小。该结 果表明，无人机并非总能通过计算卸载节省能量。最优卸 载策略取决于计算需求和相对距离。

V. 基于梯度投影法的非线性规划

A. 约束非线性优化问题的构建

继第四节之后，我们进一步提出一种基于梯度投影机 制的非线性规划方法，以应对原问题 M3的复杂性。为 此，我们根据(1)将系统状态方程重新整理如下

s[t]= A t s[0]+ t − 1 ∑ l=0 A t − 1 − l Ba[l], t= 1,…, N. (24)

根据(24)，我们可以得到 t= 1,…, N ⎧⎨⎩x[t]= x[0]+ tΔτ v[0]+∑ t − 1 l= 0[(t −1 − l)Δ 2 τ+ 1 2 Δ 2 τ] a[l]; v[t]= v[0]+Δτ∑ − 1 l= 0 a[l]. (25)

设速度控制随时间变化的序列为a=[a[0], a[1],…, a[N −1]]T， 纵向位置随时间变化的序列为x=[x[1], x[2],…, x[N]]T，纵 向速度随时间变化的序列为v=[v[1], v[2],…, v[N]]T。我们可 以将(25)式表示为更紧凑的形式 {x= bx+ Axa; v= bv+ Ava, (26) 其中，bx和bv是两个 N × 1列向量，分别表示为bx=col {x[0]+ Δτ v[0], x[0]+ 2Δτ v[0],…, x[0]+ NΔτ v[0]}和b v= col{v[0],…, v[0]}。Ax和Av是 N ×N下三角矩阵，其第 m行第 n列的元素分别为[Ax]m,n=[(m− n) Δ2τ+ 1 2Δ 2τ] × Im≥n和[Av]m,n=Δτ × Im≥n。这里， Im≥n 定义为指示函数，当且仅当 m ≥ n时等于1，否则为0。

此外，我们将纵向位置的下界和上界分别表示为x min= col{xmin,…, xmin}和xmax= col{xmax,…, xmax}， 速度的下界和上界分别表示为vmin= col{vmin,…, vmin} 和vmax=col{vmax,…, vmax}。速度控制序列的下界和上 界分别给定为amin col{amin,…, amin}和amax col {amax,…, amax}。因此，系统状态和控制量的边界约束， 即s[t] ∈S 和a[t] ∈[amin, amax]（对于 t=1,…, N）， 可表示为 Ca ≥ b, (27) 其中，C col{Ax,−Ax,Av,−Av,IN×N,−IN×N}，常数列向量为 b col{xmin −bx,bx −xmax,vmin −bv,bv −vmax,amin,−amax}。

为了重新排列系统状态的终端约束，我们定义一个 2 × N矩阵E为 E [(N −1)Δ2τ+ 1 Δ2τ, ···, 1 2 Δ2τ Δτ, ···, Δτ] (28) 以及一个列向量e e [xf − x[0] − NΔτ v[0] v f − v[0]]. (29) 由于无人机需要到达指定的终端状态sf，即对于 t= N，s [t]= sf，我们可以利用(28)和(29)将终端等式约束表述如下 Ea= e. (30)

接下来，原问题M3 简化为以下约束优化模型，记为M4， min a : W(a)= N − 1 ∑ t=0 [Emob[t]+ h(d[t])] s.t.{ Ca ≥ b; Ea= e. (31)

B. 基于梯度投影的方法

受模型M4 中线性不等式和等式约束的启发，我们提出了一 种基于梯度投影的迭代方法 用于求解 M4的框架。其核心思想是，我们可以在目标函 数 W(a)的负梯度方向上从一个可行点a开始搜索最优解 点。当迭代的起始点位于可行域的边界时，我们可以将目 标函数的负梯度投影到相对于起始点的活跃约束的切子空 间中。因此，我们总能保证搜索方向的可行性。

设ak为迭代 k处的一个可行点，即满足M4中的Aak ≥b 和Eak= e。为了构造投影算子，我们首先构造一个行满秩矩 阵M，该矩阵由与活跃约束相关的行向量组成。假设对于ak， 有C1ak= b1和C2ak> b2,，其中C1和C2是矩阵C的两个子块， b1和b2是向量b的两个子块，即C= col{C1,C2}且b= col{b1,b2}。我们可以令M= col{C1,E}。该投影矩阵可用于 将任意 N × 1列向量投影到矩阵M的零空间中。 P= IN×N − MT(MMT)−1 M, (32) 其中IN×N是 N × N单位矩阵。对于P，我们有以下结果：

引理1: 始终成立P= PT，P= P2，且P是一个半定矩阵。

证明: 根据P(32)的表达式，容易验证P= PT和P= P2。对于任一列向量y ∈ R N×1，我们也可以观察到yTPy= y TPPy=(Py)T(Py)= ‖Py‖2 ≥ 0。这表明P是一个半定矩 阵。

设目标函数 W(a)关于a的梯度为∇aW(a)。当在可行 点ak处满足P∇aW(ak)= 0时，我们在下述定理中说明负 梯度投影到M的零空间中的可行性，即Zk= −P∇aW(ak)。

定理2： 假设ak是模型M4的一个可行点，且P由(32)给出。如果 P∇aW(ak)= 0成立，则Zk= −P∇aW(ak)必为一个下降可行方向。

证明： 根据引理1，我们可以看出 (∇aW(ak)) T Zk= −(∇aW(ak)) T P∇aW(ak) = −‖P∇aW(ak)‖ 2 ≤ 0, (33) 这表明Zk是迭代次数的下降方向。此外，还可以看出 MZk= −MP∇aW(ak) = −M(IN×N − M T (MM T ) −1 M)∇aW(ak) =(−M+ M)∇aW(ak) = 0, (34) 这意味着C1Zk = 0和EZ k = 0。根据条件，C2ak >b2,， 必须存在一个正实数λ max > 0，使得对于所有 λ ∈[0, λmax]， C2(ak + λZk) ≥ b2 . (35) 由于C1 Z k = 0和C1 a k = b 1 ,，我们还得到 C 1(ak + λZ k) = b 1 . (36) 因此，结合(35)和(36)可以得到 C(ak + λZ k) ≥ b. (37)

根据EZk= 0和Eak=e，以下方程也成立 E(ak+ λZk)= e. (38) 结合(37)和(38)可以证明方向Zk的可行性。

此外，基于(35)并结合b2 −C2ak< 0，我们进一步推 导出步长 λ, λmax上界的闭式表达式，如下所示 λmax={min{[b2−C2ak]l [C2Zk]l :[C2Zk]l< 0}, C2Zk 0; +∞, C2Zk ≥ 0. (39) 在(39)中，C2Zk 0意味着向量C2Zk中至少存在一个负 分量。在这种情况下， λ的上界是有限的，而当C2Zk的 所有分量均为正时， λ可以是任意正实数。相应地，我 们可以构造一个新的迭代点ak+1，如下所示 ak+1= ak+ λZk (40) 对于 λ ∈[0, λmax] 和Zk= 0。

另一方面，在P∇aW(ak)= 0的这种情况下，定理2 可能不成立。此时，我们需要构造另一个投影矩阵，而不 是直接使用P。具体而言，我们令Q为 Q=(MMT) −1 M∇aW(ak)=[w1 w2] , (41) 其中w1和w2是W的两个子块，其行索引分别对应于C1 和E的行索引。然后，我们得到以下结果。

定理3: 假设ak是模型M4的一个可行点，且P由 (32)给出。如果P∇aW(ak)= 0成立，则有 i) 如果w1 ≤ 0，则ak必为模型M4的一个局部最优解（KKT点）； ii) 如果在w1,中存在负分量，则可以通过移除与̂w1, 中负分量对应的行索引来构造一个新的系数̂矩阵C1 ，并 可定义一个新的投影矩阵P为 P̂= IN×N −M̂ T(M̂M̂ T) −1 M̂, (42) 其中̂M col{ ̂C1 , E}。令 ̂Z k = −̂P∇a W(ak) 。 ̂Z k 必须是 一个下降可行方向。

证明： 在第一种情况（i）中，由于P∇a W(ak) = 0，我们可以 得到 0= P∇a W(ak) =[IN×N − M T (MM T ) −1 M]∇a W(ak) = ∇ a W(ak) − M T (MM T ) − 1 M∇a W(ak) = ∇ a W(ak) − C T 1 w1 − E T w2 . (43) 根据w1 ≥ 0，(43)与KKT条件一致，其中w1可被视为对 应于不等式约束的非负拉格朗日乘子。因此，a k 是一个 KKT点。

在情况(ii)中，设[w1]l < 0为w1 中的一个负分量。我们首先用 反证法证明 ̂ ̂P∇aW(ak)= 0必须 成立。假设P∇aW(ak)= 0。我们可以看出 0= P̂∇aW(ak)=[IN×N −M̂T(M̂M̂T)−1M̂]∇aW(ak) = ∇aW(ak)−M̂ T Q̂, (44) 其中 ̂Q定义为 ̂Q=(̂M̂MT)−1̂M∇aW(ak)。设 C1的第l行为[C1]l。由于 CT 1 w1+ ETw2= ĈT 1 ŵ1+[w1]l[C1]Tl+ ETw2 = M̂TQ+[w1]l[C1]Tl, (45) 其中 ̂w1是由w1中除[w1]l以外的分量组成的向量。Q定 义为Q col{̂w1, w2}。现在，将(45)代入(43)可得 0= ∇aW(ak)−M̂ TQ−[w1]l[C1]Tl. (46) 此外，由(44)减去(46)可得 0= M̂T(Q− Q̂)+[w1]l[C1]Tl. (47) 注意，(47)的右侧项确实是矩阵M中各行的线性组合。 由于组合系数为[w1]l= 0，因此(47)表明M的行向量 线性相关。这一结论与M 是行满秩的事实相矛盾。此时， 在P∇aW(ak)= 0的假设下出现了矛盾。由此确认̂P ∇aW(ak)= 0。 ̂由于P∇aW(ak)= 0，可以看出 ∇aW(ak) TẐk= −∇aW(ak) T P̂∇aW(ak) = − ∥ ∥ ∥ P̂∇aW(ak) ∥ ∥ ∥ 2 ≤ 0, (48) ̂这意味着Zk是一个下降方向。此外，我们还可以观察到 M̂Ẑk= −M̂P̂∇aW(ak) = −M̂[IN×N −M̂ T(M̂M̂T) −1 M̂]∇aW(ak) = −[M̂−M̂]∇aW(ak)= 0. (49) ̂ ̂当M= col{C1 ,E}时，(49)表明 Ĉ1 Ẑ k = 0, EẐ k = 0. (50) 将(46)的两边同时乘以[C1]l P，可得 0=[C1]l P̂∇a W(ak) −[C1]l P̂M̂ T Q−[w1]l[C1]l P̂[C1] T l . (51) 回顾 ̂P ̂ M T = 0和 ̂Zk = − ̂ P∇ a W(ak) ，我们进一步得到 0=[C1]l Ẑ k +[w1]l[C1]l P̂[C1] T l . (52) 由于P是半定的且[w1]l < 0，可以从(52)得出 [C1]l ̂ Z k = −[w1] l [C1]l ̂ P[C1] T l ≥ 0. (53)

结合(53)和(50)可得 C1 Ẑk ≥ 0, EẐk= 0. (54) 因此，按照定理2和(55)中的相同逻辑，我们̂也可以证明 Z k能够保证下降方向的可行性。

算法1总结了基于定理2和定理3所提出的基于梯度投 影的迭代算法。在算法1中，我们用Kmax表示最大迭代次 数，用 ε ∈(0,1)表示容许的数值误差。

C. 复杂度分析

从算法1可以看出，所提出的基于梯度投影的方法的计算复 杂度是 由两部分主导：可行投影矩阵P的构造以及用于获取最优 下降步长 λopt的线搜索。对于构造投影矩阵的程序，在最 坏情况下，可能需要在IF‐THEN块中多次进行矩阵修改。 投影矩阵修改的主要计算复杂度在于计算矩阵Q。设 M为 矩阵M的行数。我们可以得到 M ≤(6N+ 2)，因为M= col{C1,E}，其中C1是C的一个子块， ∈ R6N×N且E ∈ E 2×N。注意，矩阵转置MT、矩阵求逆(MMT)−1、矩阵乘法 (MMT)和(MMT)−1M、矩阵与向量乘法(MMT)−1M∇aW (ak)的计算复杂度分别为O(MN)、 O(M3)、 O(2 M2 N) 和 O(MN)。因此，在最坏情况下，投影矩阵修改的复杂 度为O(MN+ M3+ 2 M2N+ MN)。类似地，计算P的计 算复杂度数量级为 O(2MN+ M3+ 2 M2N+ N2M+ N2)。 因此，在算法V‐B的内层WHILE‐DO循环中最多需要进行 M次矩阵修改的最坏情况下，可行投影矩阵构造的复杂度 为 O(M(2MN+ M3+ 2 M2N+ N2M+ N2))。此外，对 于求解最优步长λopt的线搜索，使用牛顿一阶方法[41]达 到 ε‐最优性的复杂度数量级为O(ε−2)。在算法V‐B的外层 WHILE‐DO循环中进行 Kmax次迭代的情况下，所提方法 的整体最坏情况计算复杂度大约为 O(KmaxM(2MN+ M3+ 2 M2N+ N2M+ N2)+ Kmaxε −2)。至此，所提方 法能够高效实现多项式复杂度。需要注意的是，上述最坏 情况计算复杂度是所提方法实际复杂度的上界，而在实际 应用中，活跃矩阵M的稀疏性及其他因素可显著降低计算 复杂度。

此外，值得注意的是，所提出的方法仅需为存储决策 向量ak ∈R N×1、约束系数矩阵C ∈R 6N×N和E ∈ R 2×N、 列向量b ∈ R 6N×1、梯度向量∇aW(ak) ∈ R N×1、激活和 投影矩阵M ∈R M×N 和P ∈ R N×N，以及其他如Zk ∈ RN×1、Q ∈ R M×1、IN×N等分配内存。在算法迭代过程 中，所有相关决策和参数的预分配空间保持不变。根据上 述决策和参数的大小，其空间复杂度为 O( 11N+ 8 N2+ MN+ M)量级。此外，所有固定大小参数， 包括e、λ o p t、 λ max、 k、 Kmax，其空间复杂度均为 O (1)。在实际的计算机编程中，可通过内存管理技术（例 如著名的写时复制（COW）技术）对矩阵型或向量型参 数的预分配空间进行本地重用或共享，从而实际降低空间 复杂度。

VI. 性能评估

在本节中，我们评估所提出的无人机在基于A2G的计 算卸载场景中的联合优化方法的性能，其中假设无人机

最优纵向轨迹。(b) 最优纵向速度。)

在道路交通网络上巡航，并与路侧单元（即网络边缘）协 作处理诸如实时空中感知数据等计算密集型任务。无人机 需要联合优化其通信功率、计算卸载率和纵向加速度，以 在满足巡航运动约束的同时最大化其能量效率。在仿真场 景中，首先验证所提算法的收敛性能，然后将其全局性能 与其他几种方法进行比较。关于无人机运动学、物理层通 信和本地计算的基本仿真参数见表II，此处也采用这些参 数进行实验。

A. 收敛性分析

为了验证所提方法的收敛性，我们考虑一架旋翼无人 机沿指定初始和终端速度及位置的纵向轨迹飞行。飞行持 续时间为30秒，所有 t的计算需求设置为D[t]= 2 × 106比 特。此外，我们将无人机的终端速度限制为 v[tf]= 1 (m/s)，同时改变其初始速度 v[0]以模拟不同情况，即设 置 v[0] ∈{1, 5, 10, 15}(m/s)。图5展示了所提出的联合优 化方法在不同初始速度下的收敛性能。可以看出，由于初 始速度的不同，算法收敛到的全局目标函数的稳态值也各 不相同，且初始速度越大，与移动性相关的能量消耗越多。 此外，即使初始速度设置在不同情况下，所提出的方法也 显示出经过少数迭代次数后即可有效收敛。也就是说，在 所有情况下，仅需10次迭代即可满足收敛的一阶最优性条 件。

最优功率控制。(b) 最优速度控制。)

在图6中，展示了无人机飞行过程中的最优纵向轨迹 和速度。从图6.(a)和图6.(b)可以看出，无人机首先加速 至最优巡航速度，然后以恒定速度飞行。当接近终端位置 时，无人机减速至指定的终端速度。此外，不同初始速度 下的无人机最优巡航速度也有所不同。在图7中，展示了 通过空对地无线链路进行计算卸载的最优传输功率以及飞 行过程中的最优速度控制。可以观察到，当无人机与路侧 单元之间的相对距离较大时，即在初始阶段无人机正在接 近路侧单元上方区域（加速阶段）或在最后阶段远离路侧 单元（减速阶段），无人机必须采用最大传输功率，以尽 可能多地卸载其计算任务。当相对距离减小到一定范围内， 即 t在(150420)之间时，功耗也随之下降。主要原因是当 无人机更靠近路侧单元时，空对地通信链路质量变得更好。 图7.(b)中的最优速度控制曲线证实了无人机始终能够满足 控制约束，并表明无人机分别采用最大加速度和最大减速 度来达到最优巡航速度和指定的终端速度。

为了说明无人机的卸载行为，我们进一步评估了图8 中与本地计算相关的计算能耗。有趣的是，我们可以看到， 当 t ∈(150,420)时，计算能耗E com[t]降至零。该结果表明， 当无人机在靠近路侧单元的一定范围内飞行时，能够将其 全部计算任务卸载到路侧单元，并完全采用远程计算模式。 但当无人机飞离

从路侧单元（RSU）来看，例如在 t ∈(500600)处，传输功 率增加，仅有一部分计算任务可以卸载到路侧单元。综上所 述，上述图表结果验证了所提方法的收敛性和可行性，并表 明该方法能够使无人机在飞行过程中自适应地调整其移动性、 通信和计算。

B. 性能比较

为了展示所提出方法的优势，我们进一步在不同情况 下进行了一系列实验以比较性能。具体而言，我们将我们 的方法与另外三种基于激进移动机制、激进卸载机制和本 地计算机制的传统方法进行了对比。为简便起见，我们提 出的方法对应的数值结果标记为“联合优化”或“JO”， 而其他方法分别标记为“激进移动”或“AM”、“激进 卸载”或“AO”以及“本地计算”或“LC”。在激进移 动机制下，无人机将以最大加速度加速至最大允许速度， 并将该速度作为其巡航速度。在这种情况下，无人机的轨 迹未被优化。在激进卸载机制下，无人机将始终采用其最 大允许传输功率进行计算卸载，并考虑联合优化移动性和 计算能耗。在本地计算机制下，无人机仅优化其移动性， 并完全采用本地计算模式处理其全部计算需求。

图9展示了在不同计算需求 D[t]下，各对比方法的全 局性能 W(a)。具体而言， D[t]从 103比特变化到 4 × 106 比特。飞行时长设定为30秒，初始速度和终止速度均指定 为v[0]= v[tf]= 1(m/s)。从图9可以看出，在所有需求情 况下，无优化的激进移动机制能耗最高，而其他方法的全 局能耗处于同一数量级。然而，将我们提出的方法与激进 卸载和本地计算方法相比，可以发现所提出的联合优化方 法在不同计算需求下均能实现最低的能耗。我们的方法在 全球能耗上平均分别比激进卸载和本地计算方法低约 14.3502（焦耳）和约77.0035（焦耳）。此外，图9表明， 当计算需求为

当计算需求相对较大时，例如 D[t] ≥ 3 × 106比特，激进 卸载机制的性能趋向于接近我们提出的方法。这是因为当 计算需求大幅增加时，无人机需要提高其用于计算卸载的 传输功率，以从远程计算中获益。

我们还在不同的飞行持续时间下将我们的方法与其他 方法进行了比较。数值结果如图10所示。可以看出，增加 飞行时长能够降低整体能量消耗，符合预期。在所有情况 下，激进移动的表现最差，因为它未采用任何优化机制。 然而，我们的方法始终实现了最低的全局能耗。例如，图 10的右子图展示了在70秒飞行时长下除激进移动方法外其 他方法数值结果的细节。在所有持续时间设置中，与激进 卸载和本地计算方法相比，我们提出的联合优化方法平均 可分别减少约29.7433（焦耳）和75.8256（焦耳）的能 耗。

最后，为了展示初始速度和终端速度对全局性能的影 响，我们分别将初始速度 v[0]和终端速度v[tf]从1（米/秒） 变化到19（米/秒），增量步长2（米/秒），并比较不同 方法的效果。图11和图12 展示了它们的数值结果。结果表明，增加初始速度或终端 速度会增加与移动性相关的能耗。两幅图还表明，我们提 出的方法在所有对比方法中实现了全局能耗的最大降低。 特别是在图11中，与激进卸载和本地计算方法相比，我们 提出的方法平均分别减少了约10.9126（焦耳）和 80.7331（焦耳）的能耗。类似地，在图12中，与这两种 优化方法相比，我们提出的方法平均分别实现了约 10.9027（焦耳）和80.6835（焦耳）的节能。这些结果证 实，联合优化无人机的移动性、通信和计算比仅规划无人 机轨迹或仅优化计算卸载或传输功率更具优势。

VII. 结论与未来工作

本文研究了空地一体化网络中面向无人机的轨迹优化、 功率控制与计算卸载问题。提出了一种联合移动性、通信 与计算优化方法，以最大化无人机的能量效率。为应对优 化复杂性，提出了原始分解方法，并理论推导出最优功率 控制的闭式表达式。进而，利用该闭式功率控制将原始联 合优化模型转化为另一种可处理形式。基于转换后的模型， 提出了一种新颖的基于梯度投影的方法，并从理论上证明 了其可行性与收敛性。对比仿真结果验证了所提方法的有 效性与优势。本工作可为空地一体化场景中的无人机联合 控制与优化建模提供有价值的参考。未来，我们将聚焦于 车‐路‐无人机一体化系统的联合优化框架设计。