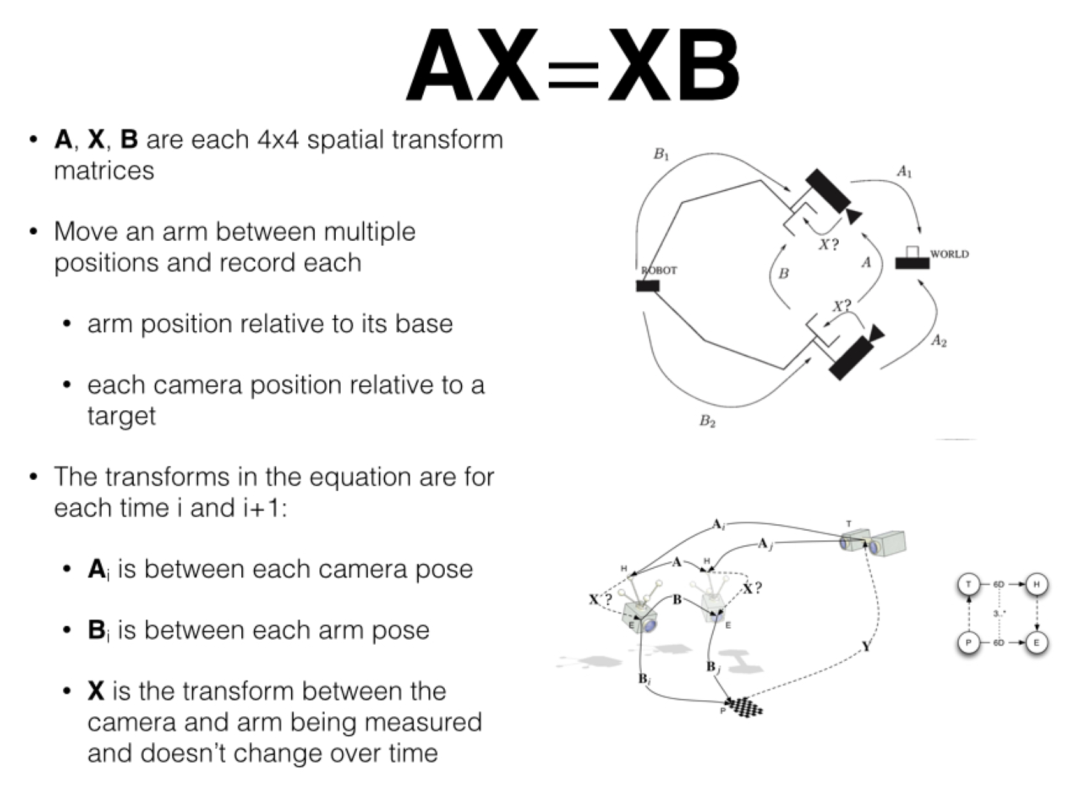







(图1)
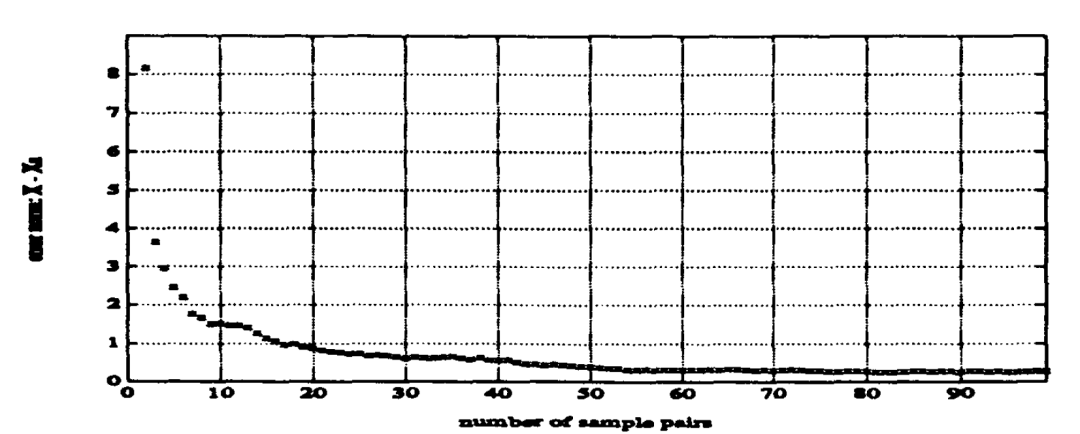
图标题: 图1. 添加小噪声后,k个样本的误差。
y轴: 误差 (η_rot)
x轴: 样本对数量
(图2)
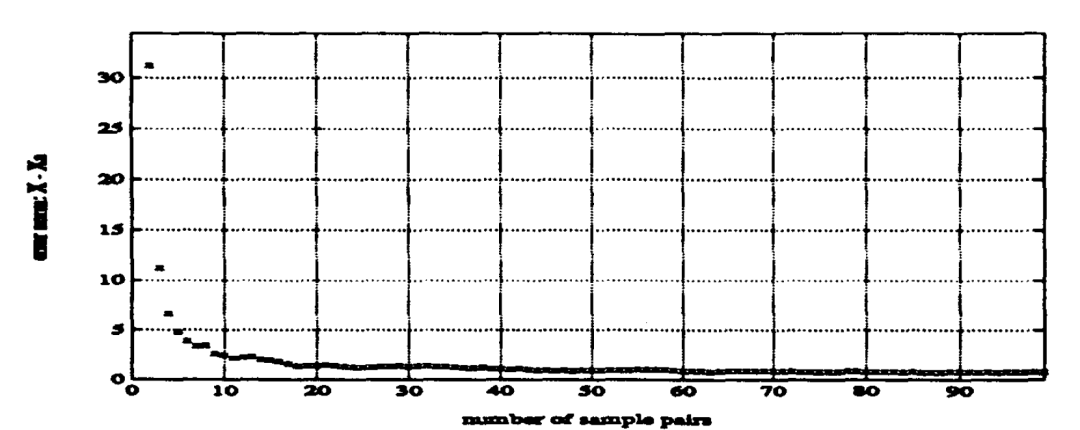
图标题: 图2. 添加大噪声后,k个样本的误差。
y轴: 误差 (η_rot)
x轴: 样本对数量

参考文献
[1] R. W. Brockett, "Least squares matching problems," Linear Algebra and Its Applications, vol. 124, pp. 761-777, 1989.
[2] C. Chevalley, Theory of Lie Groups. Princeton, NJ: Princeton University Press, 1946.
[3] J. C. K Chou and M. Kamel, "Finding the position and orientation of a sensor on a robot manipulator using quaternions," Int. J. Robotics Res., vol. 10, pp. 240-254, 1991.
[4] M. L. Curtis, Matrix Groups. New York: Springer-Verlag, 1984.
[5] F. R. Gantmacher, Matrix Theory. New York: Chelsea, 1960.
[6] A. Nádas, "Least squares and maximum likelihood estimation of rigid motion," IBM Research Report RC6945, IBM, Yorktown Heights, NY, 1978.
[7] F. C. Park, A. P. Murray, and J. M. McCarthy, "Designing mechanisms for workspace fit," in Computational Kinematics, J. Angeles, G. Hommel, and P. Kovacs, Eds. Amsterdam: Kluwer, 1993.
[8] Y. C. Shiu and S. Ahmad, "Calibration of wrist-mounted robotic sensors by solving homogeneous transform equations of the form AX=XB," IEEE Trans. Robotics Automat., vol. 5, pp. 16-27, 1989.
MATLAB

function X = park(A,B) % function X = park(A,B) 定义一个名为 park 的函数,输入参数为 A 和 B,输出为 X。% Calculates the least squares solution of % 计算最小二乘解% AX = XB % AX = XB% From % 该方法源于论文:% Robot Sensor Calibration: % 机器人传感器标定:% Solving AX=XB on the Euclidean Group % 求解欧几里得群上的AX=XB% M. Park % 作者:F.C. Park% %% Mili Shah % 编者:Mili Shah% July 2014 % 日期:2014年7月[m,n] = size(A); % 获取输入矩阵 A 的尺寸,m 是行数,n 是列数。n = n/4; % 计算测量对 (A_i, B_i) 的数量。因为每个 A_i 是 4x4 的,它们水平堆叠在一起,所以总列数要除以4。M = zeros(3,3); % 初始化一个 3x3 的零矩阵 M,用于累加计算旋转分量,即 M = Σ(β_i * α_i')。a1 = zeros(3,n); % 初始化一个 3xn 的矩阵 a1,用于存储所有 A_i 的旋转向量 α_i。b1 = zeros(3,n); % 初始化一个 3xn 的矩阵 b1,用于存储所有 B_i 的旋转向量 β_i。%Calculate best rotation R % 计算最佳旋转矩阵 Rfor i = 1:n % 开始一个循环,遍历每一对测量数据 (A_i, B_i)。 A1 = logm(A(1:3,4*i-3:4*i-1)); % 提取第 i 个测量矩阵 A_i 的 3x3 旋转部分,并计算其矩阵对数,得到一个斜对称矩阵。 B1 = logm(B(1:3,4*i-3:4*i-1)); % 提取第 i 个测量矩阵 B_i 的 3x3 旋转部分,并计算其矩阵对数,得到一个斜对称矩阵。 a1(:,i) = [A1(3,2) A1(1,3) A1(2,1)]'; % 从斜对称矩阵 A1 中提取旋转向量 α_i 的三个分量,并将其存为列向量。 b1(:,i) = [B1(3,2) B1(1,3) B1(2,1)]'; % 从斜对称矩阵 B1 中提取旋转向量 β_i 的三个分量。 M = M + b1(:,i)*a1(:,i)'; % 累加计算矩阵 M,即 M = Σ(β_i * α_i')。注意这里原文公式是 Σ(α_i * β_i'),代码实现有出入,但最终结果形式一致。end % 循环结束。[u,v] = eig(M'*M); % 计算矩阵 M' * M 的特征值分解。u 是特征向量矩阵,v 是包含特征值的对角矩阵。v = diag(diag(v).^(-1/2)); % 计算对角矩阵 v 中每个特征值的负二分之一幂,这是计算 (M'*M)^(-1/2) 的一部分。R = u*v*u'*M'; % 根据公式 R_X = (M'*M)^(-1/2) * M' 计算最优旋转矩阵 R。(注意:原文公式为 (M^T*M)^(-1/2)*M^T,代码实现了等价形式)%Calculate best translation t % 计算最佳平移向量 tC = zeros(3*n,3); % 初始化一个 (3n)x3 的零矩阵 C,用于构建线性方程组 Ct=d 的左侧矩阵。d = zeros(3*n,1); % 初始化一个 (3n)x1 的零向量 d,用于构建线性方程组的右侧向量。I = eye(3); % 创建一个 3x3 的单位矩阵 I,方便后续使用。for i = 1:n % 开始另一个循环,遍历每个测量对以构建 C 和 d。 C(3*i-2:3*i,:) = I - A(1:3,4*i-3:4*i-1); % 填充矩阵 C 的第 i 个块,该块等于 I - Θ_Ai。 d(3*i-2:3*i,:) = A(1:3,4*i)-R*B(1:3,4*i); % 填充向量 d 的第 i 个块,该块等于 b_Ai - R_X * b_Bi。end % 循环结束。t = C\d; % 求解线性最小二乘问题 Ct=d,得到最优平移向量 t。%Put everything together to form X % 将旋转和平移组合成最终的变换矩阵 XX = [R t;0 0 0 1]; % 将计算出的旋转矩阵 R 和平移向量 t 组合成一个 4x4 的齐次变换矩阵 X。
Python

from scipy.linalg import sqrtm # 从 scipy.linalg 库中导入 sqrtm 函数,用于计算矩阵的平方根。from numpy.linalg import inv # 从 numpy.linalg 库中导入 inv 函数,用于计算矩阵的逆。import numpy # 导入 numpy 库,用于进行科学计算,特别是多维数组操作。from numpy import dot, eye, zeros, outer # 从 numpy 库中导入常用的函数:dot(点积), eye(单位矩阵), zeros(零矩阵), outer(外积)。from numpy.linalg import inv # 再次从 numpy.linalg 库中导入 inv 函数(重复导入,但不影响功能)。# 定义第一个测量对中的矩阵 A1A1 = numpy.array([[-0.989992, -0.14112, 0.000, 0], # 矩阵的第一行 [0.141120 , -0.989992, 0.000, 0], # 矩阵的第二行 [0.000000 , 0.00000, 1.000, 0], # 矩阵的第三行 [0 , 0, 0, 1]]) # 矩阵的第四行(齐次坐标)# 定义第一个测量对中的矩阵 B1B1 = numpy.array([[-0.989992, -0.138307, 0.028036, -26.9559], # 矩阵的第一行 [0.138307 , -0.911449, 0.387470, -96.1332], # 矩阵的第二行 [-0.028036 , 0.387470, 0.921456, 19.4872], # 矩阵的第三行 [0 , 0, 0, 1]]) # 矩阵的第四行(齐次坐标)# 定义第二个测量对中的矩阵 A2A2 = numpy.array([[0.07073, 0.000000, 0.997495, -400.000], # 矩阵的第一行 [0.000000, 1.000000, 0.000000, 0.000000], # 矩阵的第二行 [-0.997495, 0.000000, 0.070737, 400.000], # 矩阵的第三行 [0, 0, 0,1]]) # 矩阵的第四行(齐次坐标)# 定义第二个测量对中的矩阵 B2B2 = numpy.array([[ 0.070737, 0.198172, 0.997612, -309.543], # 矩阵的第一行 [-0.198172, 0.963323, -0.180936, 59.0244], # 矩阵的第二行 [-0.977612, -0.180936, 0.107415, 291.177], # 矩阵的第三行 [0, 0, 0, 1]]) # 矩阵的第四行(齐次坐标)def logR(T): # 定义一个函数 logR,用于计算旋转矩阵的对数映射,即将其转换为旋转向量。 R = T[0:3, 0:3] # 从输入的4x4齐次变换矩阵 T 中提取出3x3的旋转矩阵 R。 theta = numpy.arccos((numpy.trace(R) - 1)/2) # 根据公式计算旋转角度 theta。 logr = numpy.array([R[2,1] - R[1,2], R[0,2] - R[2,0], R[1,0] - R[0,1]]) * theta / (2*numpy.sin(theta)) # 根据罗德里格斯反变换公式,从R和theta计算出旋转向量(轴角表示)。 return logr # 返回计算得到的3x1旋转向量。def Calibrate(A, B): # 定义主标定函数 Calibrate,输入参数为A矩阵列表和B矩阵列表。 n_data = len(A) # 获取测量数据对的数量。 M = numpy.zeros((3,3)) # 初始化一个3x3的零矩阵 M,用于后续计算旋转部分。 C = numpy.zeros((3*n_data, 3)) # 初始化一个(3*n)x3的零矩阵 C,用于构建求解平移的线性方程组。 d = numpy.zeros((3*n_data, 1)) # 初始化一个(3*n)x1的零向量 d,用于构建求解平移的线性方程组。 A_ = numpy.array([]) # 初始化一个空数组 A_(此行代码在后续未使用)。
for i in range(1): # 开始一个循环,但范围是range(1),意味着这个循环只会执行一次(i=0)。 alpha = logR(A[i]) # 计算第一个A矩阵(A1)的旋转向量 alpha。 beta = logR(B[i]) # 计算第一个B矩阵(B1)的旋转向量 beta。 alpha2 = logR(A[i+1]) # 计算第二个A矩阵(A2)的旋转向量 alpha2。 beta2 = logR(B[i+1]) # 计算第二个B矩阵(B2)的旋转向量 beta2。 alpha3 = numpy.cross(alpha, alpha2) # 计算 alpha 和 alpha2 的叉积,生成一个线性无关的向量 alpha3。 beta3 = numpy.cross(beta, beta2) # 计算 beta 和 beta2 的叉积,生成对应的向量 beta3。
M1 = numpy.dot(beta.reshape(3,1),alpha.reshape(3,1).T) # 计算 beta 和 alpha 的外积 M1。 M2 = numpy.dot(beta2.reshape(3,1),alpha2.reshape(3,1).T) # 计算 beta2 和 alpha2 的外积 M2。 M3 = numpy.dot(beta3.reshape(3,1),alpha3.reshape(3,1).T) # 计算 beta3 和 alpha3 的外积 M3。 M = M1+M2+M3 # 将三个外积相加,构造出用于求解旋转的聚合矩阵 M。
theta = numpy.dot(sqrtm(inv(numpy.dot(M.T, M))), M.T) # 根据论文中的最小二乘公式,计算最优的旋转矩阵 theta (即 R_X)。 for i in range(n_data): # 开始一个循环,遍历所有的数据对来构建用于求解平移的方程组。 rot_a = A[i][0:3, 0:3] # 提取第 i 个A矩阵的旋转部分。 rot_b = B[i][0:3, 0:3] # 提取第 i 个B矩阵的旋转部分。 trans_a = A[i][0:3, 3] # 提取第 i 个A矩阵的平移部分。 trans_b = B[i][0:3, 3] # 提取第 i 个B矩阵的平移部分。
C[3*i:3*i+3, :] = numpy.eye(3) - rot_a # 填充矩阵 C 的第 i 个块,等于 I - Θ_Ai。 d[3*i:3*i+3, 0] = trans_a - numpy.dot(theta, trans_b) # 填充向量 d 的第 i 个块,等于 b_Ai - R_X * b_Bi。
b_x = numpy.dot(inv(numpy.dot(C.T, C)), numpy.dot(C.T, d)) # 使用正规方程法求解线性最小二乘问题 Ct=d,得到最优平移向量 b_x。 return theta, b_x # 返回计算出的最优旋转矩阵 theta 和平移向量 b_x。X = numpy.eye(4) # 初始化最终结果X为一个4x4的单位矩阵。A = [A1, A2] # 将输入的A矩阵放入一个列表中。B = [B1, B2] # 将输入的B矩阵放入一个列表中。theta, b_x = Calibrate(A, B) # 调用 Calibrate 函数,传入数据并获取计算结果。X[0:3, 0:3] = theta # 将计算出的旋转矩阵 theta 填充到 X 的左上角3x3部分。X[0:3, -1] = b_x.flatten() # 将计算出的平移向量 b_x 展平并填充到 X 的最后一列的前三行。print("X: ") # 打印一个标签 "X: "。print(X) # 打印最终计算出的手眼标定矩阵 X。
C++ (opencv)

// 定义一个静态函数 calibrateHandEyePark,用于执行Park-Martin手眼标定算法。// 输入参数:// Hg: 一个包含多个机械臂末端姿态(gripper pose)的向量,每个姿态为4x4的Mat矩阵。// Hc: 一个包含多个相机姿态(camera pose)的向量,每个姿态为4x4的Mat矩阵。// 输出参数 (通过引用传递):// R_cam2gripper: 计算出的相机到夹爪的3x3旋转矩阵。// t_cam2gripper: 计算出的相机到夹爪的3x1平移向量。static void calibrateHandEyePark(const std::vector<Mat>& Hg, const std::vector<Mat>& Hc, Mat& R_cam2gripper, Mat& t_cam2gripper){ Mat M = Mat::zeros(3, 3, CV_64FC1); // 初始化一个3x3的零矩阵 M,用于累加计算旋转分量,类型为64位浮点数。 for (size_t i = 0; i < Hg.size(); i++) // 开始外层循环,遍历所有姿态。 { for (size_t j = i+1; j < Hg.size(); j++) // 开始内层循环,将第i个姿态与之后的所有姿态配对。 { // 通过配对(i, j)来计算相对运动。 // gripper的相对运动 A_ij = (Hg_j)^-1 * Hg_i Mat Hgij = homogeneousInverse(Hg[j]) * Hg[i]; // camera的相对运动 B_ij = Hc_j * (Hc_i)^-1 (注意这里的顺序) Mat Hcij = Hc[j] * homogeneousInverse(Hc[i]); Mat Rgij = Hgij(Rect(0, 0, 3, 3)); // 从gripper的相对运动矩阵中提取3x3的旋转矩阵。 Mat Rcij = Hcij(Rect(0, 0, 3, 3)); // 从camera的相对运动矩阵中提取3x3的旋转矩阵。 Mat a, b; // 定义两个Mat变量 a 和 b,用于存储旋转向量。 Rodrigues(Rgij, a); // 使用 Rodrigues 反变换,将旋转矩阵 Rgij 转换为旋转向量 a (即 α_ij)。 Rodrigues(Rcij, b); // 使用 Rodrigues 反变换,将旋转矩阵 Rcij 转换为旋转向量 b (即 β_ij)。 M += b * a.t(); // 累加计算聚合矩阵 M,即 M = Σ(β_ij * α_ij')。 } } Mat eigenvalues, eigenvectors; // 定义用于存储特征值和特征向量的矩阵。 eigen(M.t()*M, eigenvalues, eigenvectors); // 计算 M的转置乘以M (M'M) 的特征值和特征向量。 Mat v = Mat::zeros(3, 3, CV_64FC1); // 初始化一个3x3的对角矩阵 v。 for (int i = 0; i < 3; i++) { // 循环遍历三个特征值。 v.at<double>(i,i) = 1.0 / sqrt(eigenvalues.at<double>(i,0)); // 计算特征值的负二分之一幂,并填充到v的对角线上,以构造 (M'M)^(-1/2) 的一部分。 } // 根据公式 R = (M'M)^(-1/2) * M' 计算最优旋转矩阵。 // 这里 (M'M)^(-1/2) 通过特征分解 U * Λ^(-1/2) * U' 来计算。 Mat R = eigenvectors.t() * v * eigenvectors * M.t(); R_cam2gripper = R; // 将计算出的最优旋转矩阵 R 赋值给输出参数。 // 计算总共有多少个(i, j)配对,用于确定C和d矩阵的行数。 int K = static_cast<int>((Hg.size()*Hg.size() - Hg.size()) / 2.0); Mat C(3*K, 3, CV_64FC1); // 初始化一个 (3K)x3 的矩阵 C,用于构建求解平移的线性方程组的左侧。 Mat d(3*K, 1, CV_64FC1); // 初始化一个 (3K)x1 的向量 d,用于构建线性方程组的右侧。 Mat I3 = Mat::eye(3, 3, CV_64FC1); // 创建一个3x3的单位矩阵 I。 int idx = 0; // 初始化一个索引,用于在C和d矩阵中定位填充位置。 for (size_t i = 0; i < Hg.size(); i++) // 再次开始外层循环,遍历所有姿态。 { for (size_t j = i+1; j < Hg.size(); j++, idx++) // 再次开始内层循环,生成与计算旋转时完全相同的相对运动对。 { // 重新计算第(i, j)对的相对运动。 Mat Hgij = homogeneousInverse(Hg[j]) * Hg[i]; Mat Hcij = Hc[j] * homogeneousInverse(Hc[i]); Mat Rgij = Hgij(Rect(0, 0, 3, 3)); // 提取gripper相对运动的旋转部分 Rgij。 Mat tgij = Hgij(Rect(3, 0, 1, 3)); // 提取gripper相对运动的平移部分 tgij。 Mat tcij = Hcij(Rect(3, 0, 1, 3)); // 提取camera相对运动的平移部分 tcij。 Mat I_tgij = I3 - Rgij; // 计算 (I - Rgij) 块。 I_tgij.copyTo(C(Rect(0, 3*idx, 3, 3))); // 将 (I - Rgij) 块复制到大矩阵 C 的相应位置。 Mat A_RB = tgij - R*tcij; // 计算 (tgij - R*tcij) 块。 A_RB.copyTo(d(Rect(0, 3*idx, 1, 3))); // 将 (tgij - R*tcij) 块复制到大向量 d 的相应位置。 } } Mat t; // 定义一个Mat变量 t,用于存储求解出的平移向量。 // 求解超定线性方程组 Ct = d,以获得最优平移向量 t。 // 使用 DECOMP_SVD (奇异值分解) 方法求解,这种方法对于病态矩阵非常鲁棒,能够找到最小二乘解。 solve(C, d, t, DECOMP_SVD); t_cam2gripper = t; // 将计算出的最优平移向量 t 赋值给输出参数。}




















 1027
1027

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








