前言
在这之前,我先说明一下代码中的几个东西:
node[pos]表示线段树上的一个点,node[pos].l和node[pos].r表示这个点代表的区间左端点和右端点。ls和rs是 left_son 和 right_son 的缩写,表示左儿子和右儿子。
线段树
在讲线段树之前,我们先来做一个看上去没什么意义的事:
已知一个序列 a a a,请问 a x a_x ax 是多少?
这个问题看上去很简单是吧,我们直接调用 a x a_x ax 就行了。时间复杂度明显是 O ( 1 ) O(1) O(1) 的。
现在我们来考虑一个复杂一点的做法:二分。
因为我们知道下标是有序的,因此我们可以二分这个下标,直到这个中间值是 x x x 时再算 a x a_x ax。时间复杂度: O ( log n ) O(\log n) O(logn)。
现在我们想象这样一个情景:一共有 m m m 次询问,每次询问给你一个 x x x,然后问你 a x a_x ax 是多少?其中 x ≤ 1 0 9 x\le10^9 x≤109。
首先数组的做法是肯定不行了,因此我们可以用二分,但每次二分听上去貌似太麻烦了,于是我们可以记录下来每次二分可能产生的区间,形成一棵树,就像归并排序一样,然后你就获得了一棵线段树:
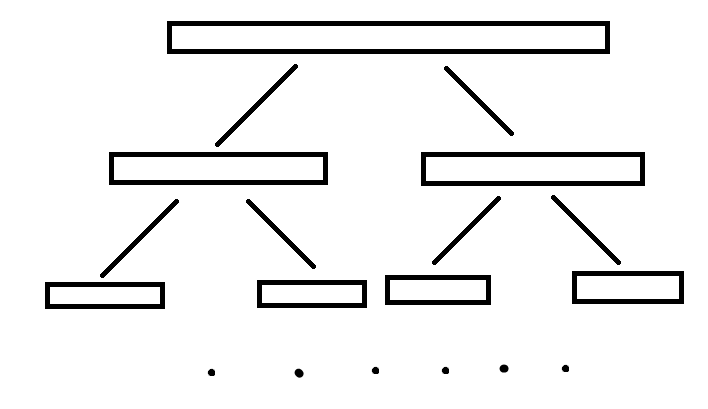
这样,每次你要找一个点的时候,只需要看看往左儿子跑还是右儿子跑就行了。
这就是线段树最基础的操作:单点查询。
代码:
int query(int pos,int x)
{
if(node[pos].l==node[pos].r)
{
return node[pos].s;
}
int ans=0;
int mid=node[pos].l+node[pos].r>>1;//因为优先级,所以可以不加括号
if(x<=mid)
{
ans=query(pos<<1,x);
}
else
{
ans=query(pos<<1|1,x);//这里相当于 (pos<<1)+1 的作用
}
return ans;
}
相应的,我们也可以单点修改:
void update(int pos,int x,int y)
{
if(node[pos].l==node[pos].r)
{
node[pos].s=y;
return;
}
int mid=node[pos].l+node[pos].r>>1;
if(x<=mid)
{
update(pos<<1,x,y);
}
else
{
update(pos<<1|1,x,y);
}
}
然后,就是稍微复杂一点的东西了:区间修改和区间查询。我们先从区间查询说起。
区间查询
假设有一个 [1,6] 的区间,现在我问你 [2,4] 内的和是多少。你肯定看一眼就知道这个东西可以用前缀和。我们现在不用前缀和,尝试用线段树,看看会怎么样。
首先我们把 [2,4] 跟 [1,6] 比,发现比它小:
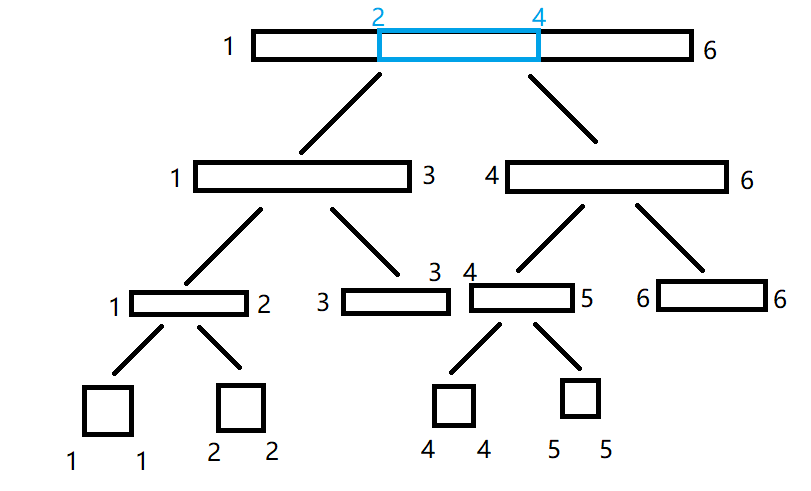
这说明我们不能用 [1,6] 区间内的和来算 [2,4] 的部分和(不然会比真实的值大),于是我们考虑把这段区间扔给它的左儿子研究:
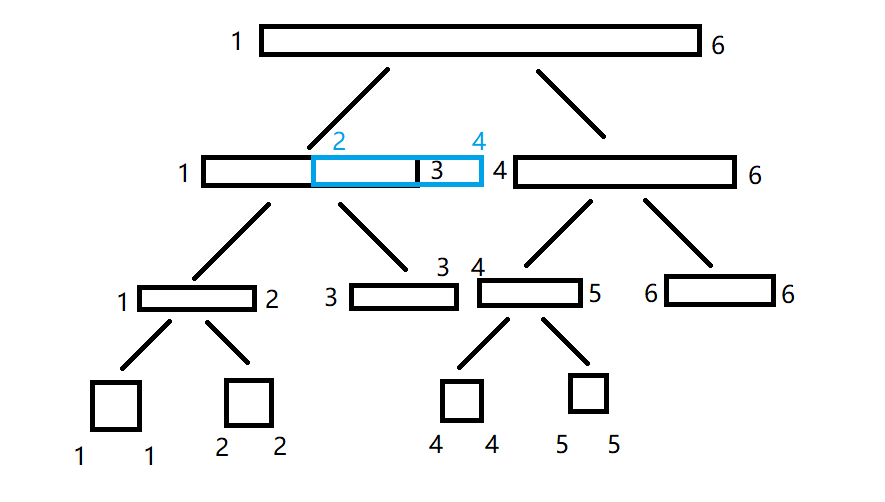
我们发现:它的左儿子也不能用它自己的区间和来算 [2,4] 的部分和(不然
a
1
a_1
a1 会被算进去),于是我们考虑把这段区间扔给它的左儿子:
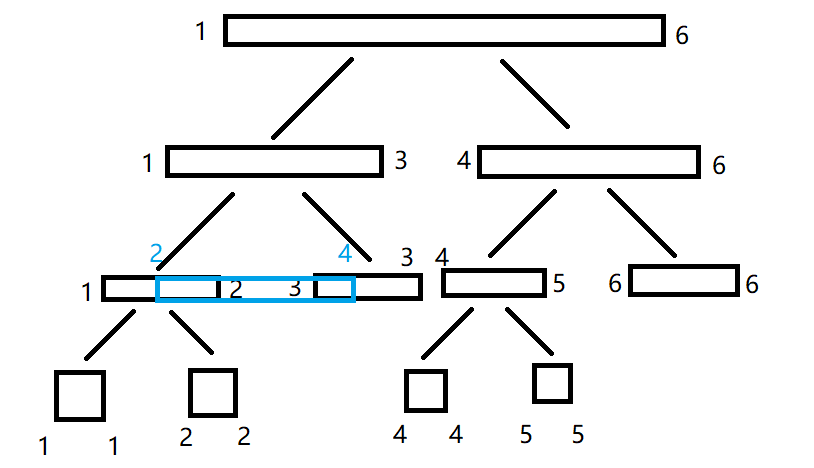
我们发现:仍然不能算。于是又把这个区间扔给它的左儿子:
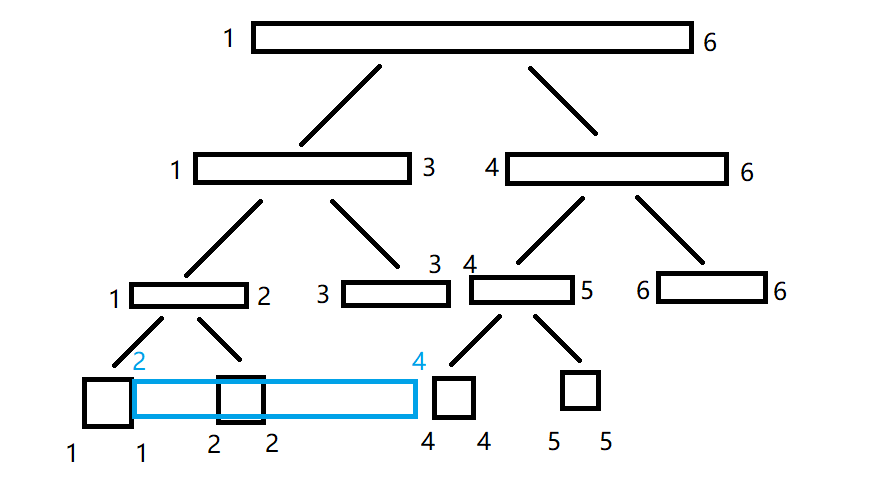
这时我们会发现一个问题:这个区间和我要求的区间完全没有交集,那我肯定不能用这段区间来算。于是回退到它的父亲节点,然后尝试用它的父亲节点的右儿子算:
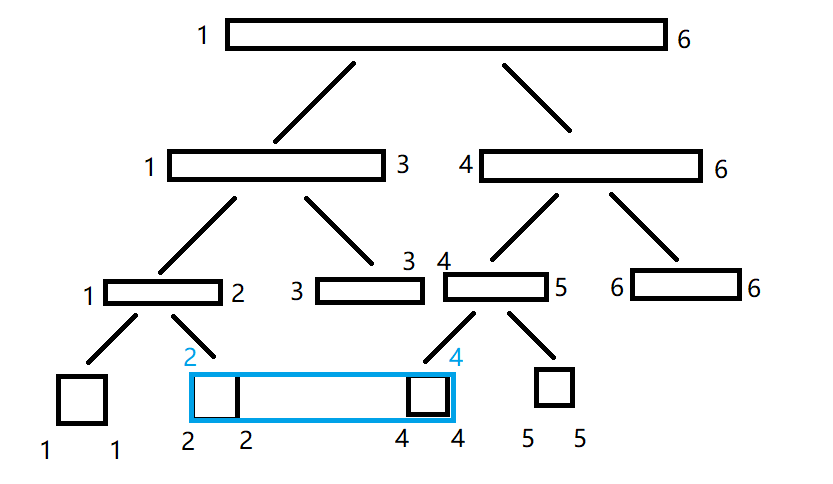
我们发现:这段区间被完美的覆盖在了我们要求的区间内,于是直接把这段区间的和加上,然后退回到父亲节点(其实到了叶子结点也说明这个点肯定被覆盖在里面了)。
然后重复上述操作很多次……
最终,你就能得到:原来区间 [2,4] 的和就是区间 [2,2]、[3,3]、[4,4] 的和的总和。于是你就能求出答案了。
代码:
int query(int pos,int l,int r)
{
if(node[pos].l>=l&&node[pos].r<=r)//被覆盖在里面了
{
return node[pos].s;//直接返回
}
int mid=node[pos].l+node[pos].r>>1,ans=0;//求左儿子的右端点
if(l<=mid)//如果和左儿子有交集
{
ans+=query(pos<<1,l,r);//这里不用调整右端点,反正右边也不会被考虑
}
if(r>mid)//与右儿子有交集
{
ans+=query(pos<<1|1,l,r);//这里其实可以换成其他东西,比如说区间最大值
}
return ans;
}
区间修改
到了区间修改这一部分,基本就有很大的调整了。
当然,最重要的思想还是沿用区间查询的思想:能偷懒就偷懒。所以这里诞生了一个新的东西:懒标记(lazy tag)。
我们继续上面的例子:如果说我现在要让区间 [4,5] 全部加上一个数
s
s
s,那我该怎么做?
如果说你找出所有在区间 [4,5] 之间的点然后把它们的值加上一个
s
s
s,这跟
O
(
n
)
O(n)
O(n) 其实没什么区别,但线段树不是这样干的:
首先判断这个区间在哪个儿子节点里面(这里就略过了,跟上面其实是一样的)。
比如说上面那张图:
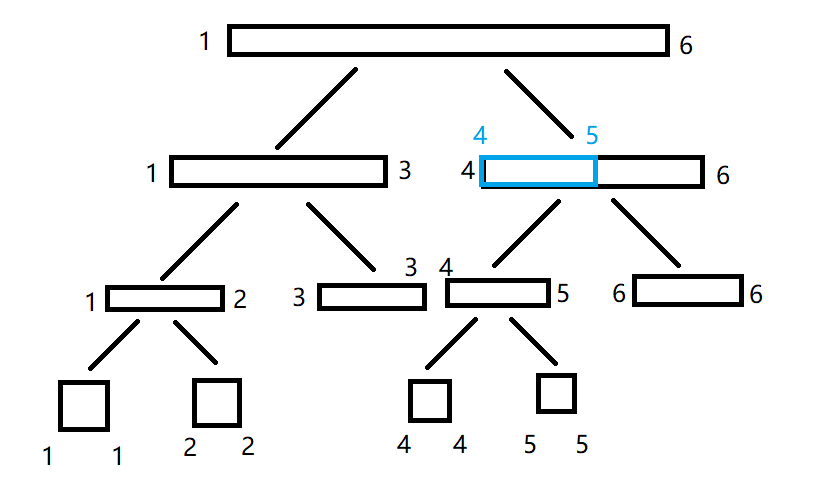
我们不难找到 [4,5] 属于右儿子。
然后我们发现这段区间并没有被覆盖进去,因此我们继续往下找:
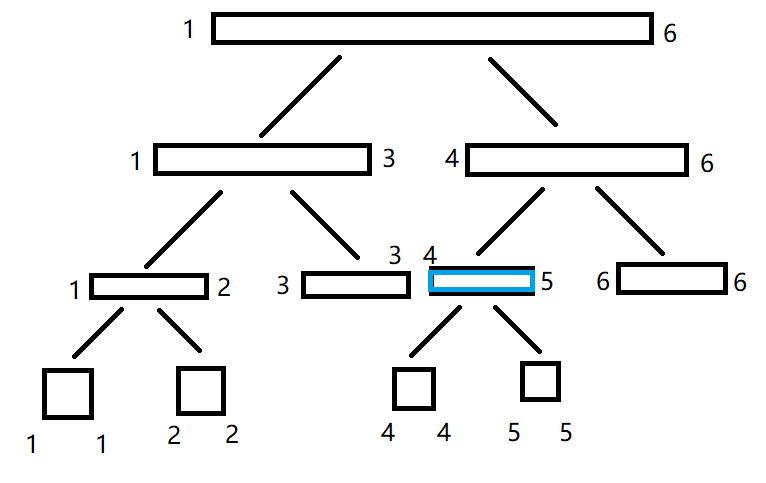
我们发现:这段区间被完美的包含在了里面,于是我们把 lazy_tag 加上
s
s
s。
然后就继续上述操作。
其实我们最终会发现:lazy_tag 的作用就是代替一段区间进行这段区间的操作。
当然我们要注意一点:如果你在扫的过程中发现这段区间原本有 lazy_tag,但是这段区间又不会被更新,那要把它的 lazy_tag 扔给它的儿子,因为这时再留在它身上就可能会导致不被更新的一边也可能会被更新,而且在后续对 query 非常不友好。
代码:
void update(int pos,int l,int r,int x)
{
if(node[pos].l>=l&&node[pos].r<=r)
{
node[pos].lt+=x;
node[pos].s+=x*(node[pos].r-node[pos].l+1);
return;
}
node[pos<<1].lt+=node[pos].lt;
node[pos<<1|1].lt+=node[pos].lt;
node[pos<<1].s+=node[pos].lt*(node[pos<<1].r-node[pos<<1].l+1);
node[pos<<1|1].s+=node[pos].lt*(node[pos<<1|1].r-node[pos<<1|1].l+1);
node[pos].lt=0;
int mid=node[pos].l+node[pos].r>>1;
if(l<=mid)
{
update(pos<<1,l,r,x);
}
if(r>mid)
{
update(pos<<1|1,l,r,x);
}
node[pos].s=node[pos<<1].s+node[pos<<1|1].s;
}
一般情况下我们为了方便,会写两个函数 pushup 和 pushdown,分别表示更新当前节点和把 lazy_tag 往下传的过程,即上面的代码也可以写成下面这样:
void pushdown(int pos,int ls,int rs)
{
if(node[pos].lt)
{
node[ls].lt+=node[pos].lt;
node[rs].lt+=node[pos].lt;
node[ls].s+=node[pos].lt*(node[ls].r-node[ls].l+1);
node[rs].s+=node[pos].lt*(node[rs].r-node[rs].l+1);
node[pos].lt=0;
}
}
void pushup(int pos,int ls,int rs)
{
node[pos].s=node[ls].s+node[rs].s;
}
void update(int pos,int l,int r,int x)
{
if(node[pos].l>=l&&node[pos].r<=r)
{
node[pos].lt+=x;
node[pos].s+=x*(node[pos].r-node[pos].l+1);
return;
}
pushdown(pos,pos<<1,pos<<1|1);
int mid=node[pos].l+node[pos].r>>1;
if(l<=mid)
{
update(pos<<1,l,r,x);
}
if(r>mid)
{
update(pos<<1|1,l,r,x);
}
pushup(pos,pos<<1,pos<<1|1);
}
结合
现在我们把上述操作结合起来,得到了三种经典模型:
- 单点修改,区间查询。
- 区间修改,单点查询。
- 区间修改,区间查询。
其中,每一种模型的函数都是不固定的,比如说第三种中 query 函数需要在每一次查询之前 pushdown 一下,这时为了方便计算,因为如果你放在父亲节点上,到时候就还得回到父亲节点时才能算,倒不如直接往下放。而且把 lazy_tag 放在父亲节点上也不好处理当前的和。当然,考虑到大部分读者时初学者,这里以区间求和为例,把三种模型的代码都写一遍:
第一种:
void pushup(int pos,int ls,int rs)
{
node[pos].s=node[ls].s+node[rs].s;
}
void update(int pos,int x,int y)
{
if(node[pos].l==node[pos].r)
{
node[pos].s=y;
return;
}
int mid=node[pos].l+node[pos].r>>1;
if(x<=mid)
{
update(pos<<1,x,y);
}
else
{
update(pos<<1|1,x,y);
}
pushup(pos,pos<<1,pos<<1|1);//这里是为了方便下面查询好找
}
int query(int pos,int l,int r)
{
if(node[pos].l>=l&&node[pos].r<=r)
{
return node[pos].s;
}
int mid=node[pos].l+node[pos].r>>1,ans=0;
if(l<=mid)
{
ans+=query(pos<<1,l,r);
}
if(r>mid)
{
ans+=query(pos<<1|1,l,r);
}
return ans;
}
第二种:
void pushdown(int pos,int ls,int rs)
{
if(node[pos].lt)
{
node[ls].lt+=node[pos].lt;
node[rs].lt+=node[pos].lt;
node[ls].s+=node[pos].lt*(node[ls].r-node[ls].l+1);
node[rs].s+=node[pos].lt*(node[rs].r-node[rs].l+1);
node[pos].lt=0;
}
}
void pushup(int pos,int ls,int rs)
{
node[pos].s=node[ls].s+node[rs].s;
}
void update(int pos,int l,int r,int x)
{
if(node[pos].l>=l&&node[pos].r<=r)
{
node[pos].lt+=x;
node[pos].s+=x*(node[pos].r-node[pos].l+1);
return;
}
pushdown(pos,pos<<1,pos<<1|1);
int mid=node[pos].l+node[pos].r>>1;
if(l<=mid)
{
update(pos<<1,l,r,x);
}
if(r>mid)
{
update(pos<<1|1,l,r,x);
}
pushup(pos,pos<<1,pos<<1|1);
}
int query(int pos,int x)
{
if(node[pos].l==node[pos].r)
{
return node[pos].s;
}
pushdown(pos,pos<<1,pos<<1|1);//为了方便后面查找
int ans=0;
int mid=node[pos].l+node[pos].r>>1;
if(x<=mid)
{
ans=query(pos<<1,x);
}
else
{
ans=query(pos<<1|1,x);
}
return ans;
}
第三种:
void pushdown(int pos,int ls,int rs)
{
if(node[pos].lt)
{
node[ls].lt+=node[pos].lt;
node[rs].lt+=node[pos].lt;
node[ls].s+=node[pos].lt*(node[ls].r-node[ls].l+1);
node[rs].s+=node[pos].lt*(node[rs].r-node[rs].l+1);
node[pos].lt=0;
}
}
void pushup(int pos,int ls,int rs)
{
node[pos].s=node[ls].s+node[rs].s;
}
void update(int pos,int l,int r,int x)
{
if(node[pos].l>=l&&node[pos].r<=r)
{
node[pos].lt+=x;
node[pos].s+=x*(node[pos].r-node[pos].l+1);
return;
}
pushdown(pos,pos<<1,pos<<1|1);
int mid=node[pos].l+node[pos].r>>1;
if(l<=mid)
{
update(pos<<1,l,r,x);
}
if(r>mid)
{
update(pos<<1|1,l,r,x);
}
pushup(pos,pos<<1,pos<<1|1);
}
int query(int pos,int l,int r)
{
if(node[pos].l==node[pos].r)
{
return node[pos].s;
}
if(node[pos].l>=l&&node[pos].r<=r)
{
return node[pos].s;
}
pushdown(pos,pos<<1,pos<<1|1);
int mid=node[pos].l+node[pos].r>>1,ans=0;
if(l<=mid)
{
ans+=query(pos<<1,l,r);
}
if(r>mid)
{
ans+=query(pos<<1|1,l,r);
}
return ans;
}
然后就大功告成了!
然后用你聪明的小脑瓜想一想就会发现:这个范围,其实可以是任何东西。不一定是下标,也可以把数当做下标来存储。
习题 + 线段树代码演示
来做一道题:洛谷 P3372 【模板】线段树 1。
这时经典的区间修改 + 区间查询,代码:
struct Tree{
struct Node{
int l,r,lt,s;
}node[400006];//注意线段树开四倍空间
void pushdown(int pos,int ls,int rs)
{
if(node[pos].lt)
{
node[ls].lt+=node[pos].lt;
node[rs].lt+=node[pos].lt;
node[ls].s+=node[pos].lt*(node[ls].r-node[ls].l+1);
node[rs].s+=node[pos].lt*(node[rs].r-node[rs].l+1);
node[pos].lt=0;
}
}
void pushup(int pos,int ls,int rs)
{
node[pos].s=node[ls].s+node[rs].s;
}
void build(int pos,int l,int r)//建树
{
node[pos].l=l,node[pos].r=r,node[pos].lt=node[pos].s=0;
if(l==r)
{
return;
}
int mid=l+r>>1;
build(pos<<1,l,mid);
build(pos<<1|1,mid+1,r);
pushup(pos,pos<<1,pos<<1|1);//注意建完树之后要更新父节点的情况
}
void update(int pos,int l,int r,int x)
{
if(node[pos].l>=l&&node[pos].r<=r)
{
node[pos].lt+=x;
node[pos].s+=x*(node[pos].r-node[pos].l+1);
return;
}
pushdown(pos,pos<<1,pos<<1|1);
int mid=node[pos].l+node[pos].r>>1;
if(l<=mid)
{
update(pos<<1,l,r,x);
}
if(r>mid)
{
update(pos<<1|1,l,r,x);
}
pushup(pos,pos<<1,pos<<1|1);
}
int query(int pos,int l,int r)
{
if(node[pos].l==node[pos].r)
{
return node[pos].s;
}
if(node[pos].l>=l&&node[pos].r<=r)
{
return node[pos].s;
}
pushdown(pos,pos<<1,pos<<1|1);
int mid=node[pos].l+node[pos].r>>1,ans=0;
if(l<=mid)
{
ans+=query(pos<<1,l,r);
}
if(r>mid)
{
ans+=query(pos<<1|1,l,r);
}
return ans;
}
}tr;
这里仅展示线段树部分的代码(事先声明一下:这份代码是我刚刚写的,没有提交过,我也不知道会不会错,反正就那个意思)。
还有,这份代码其实并不是那道题的正解,因为那道题中还要把每个节点初始化一个值,这份代码只是演示一下该怎么写线段树。
其实通过上面那个例子我们可以看出:线段树的空间复杂度很大,是 O ( 4 n ) O(4n) O(4n),它的时间复杂度本身很低,但是常数大概有四倍。
因此,下一章内容:《线段树的时间和空间优化》。





















 878
878

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








