字典树（Trie 树）详解

前言

其实本人觉得 Trie 没什么好讲的，但是为了能引出下部分内容（无奖竞猜：下一篇文章是什么？想知道答案的可以看最后），所以我决定还是单独开一篇文章讲一讲 Trie。

这篇文章将以最快速、最清晰的方式带你理解 Trie 到底干了个什么。

基础概念

我们先来看看 OI-Wiki 上是怎么解释 Trie 的：

字典树，英文名 trie。顾名思义，就是一个像字典一样的树。

额，反正意思差不多，但说的还是有点模模糊糊的，但你要我给出一个定义，我也写不来，在这里我就打个比方：

然后我们先遍历第一个字符串，把这个字符串的每一位字符都当做一条边，连向一个节点：

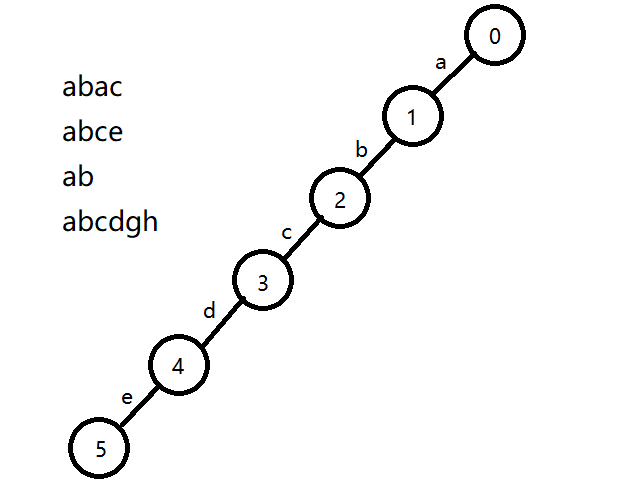
因为一条边对应的是一个字母，而字母又不好拿来当做下标，所以我们一般会按照字母表把它的编号（也就是下标）变成一个整数，如果还听不懂，可以直接看代码。

然后重复上面的操作，我们会得到这样一棵树：

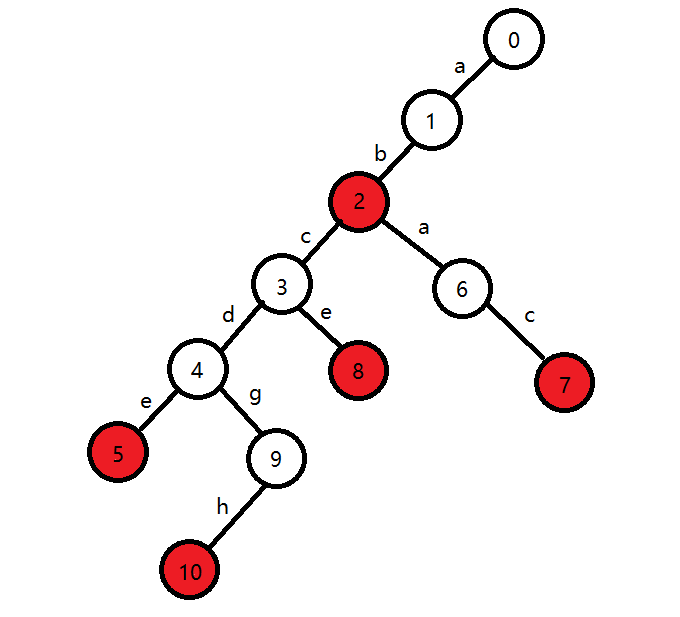
其中标红的点就是每个字符串的最后一个字母。

注意：因为字符串之间可能有重复的，所以这些红色的点一般不是直接用一个数组标记一下，而是在这个基础上加一，用来记录有多少个这样的字符串。

代码（建树）：

void push(string s)
{
	int pos=0;
	for(int i=0;i<s.size();i++)
	{
		int x=s[i]-'a';//找对应的是哪条边
		if(trie[pos][x]==0)
		{
			trie[pos][x]=++num;//如果没有这个儿子节点，就新建一个
		}
		pos=trie[pos][x];
	}
	cnt[pos]++;
}

因为建树的过程不是很好描述，没看懂上面文字的可以看代码（代码更清晰易懂一点）。

然后就是几乎每种树都要干的一件事：查询。

我们先随便遍历一下这棵 Trie 树，看看得到的字符串都是些什么：a,ab,abc,abcd,abcde,abcdg,abcdgh,abce,aba,abac。

不难发现：这些字符串都是上面我们提供的字符串中某个字符串的前缀。这一点在遍历整棵树的时候也能看出来。

所以我们就知道了 Trie 树主要解决的问题：关于字符串前缀的问题。 看上去有点废话，但它确实说明了 Trie 树的主要功能。

然后查询就很简单了：对于一个输入的字符串，主需要从前往后按照它的每一位依次往下遍历这棵树就行了。

有人会问：那它的优点在哪呢？别急，拿一道例题来你就知道了：

首先我们考虑暴力做法：一共 M 次询问，然后每次询问输入的字符串要找前缀，也就是每次询问要把前面的 N 个字符串全枚举一遍，然后对于每个字符串要遍历一遍找看前缀是否相同，总时间复杂度就是 $O(M\times N\times \mid S_i\mid )$，其中 $\mid S_i\mid$ 指 $S_i$ 的长度。很明显过不了。

但如果我们用 Trie 树呢？首先一共 M 次查询，然后每次查询要跑一遍 Trie 树，这时的时间复杂度就是 $O(\max (\mid S_i\mid ,\mid T_i\mid ))$，那么总时间复杂度就是 $O(M\times \max (\mid S_i\mid ,\mid T_i\mid ))$，如果我没算错，平均下来时间复杂度应该是 $10^7$ 左右，也就是 100ms 左右，能跑过；

实际用时：

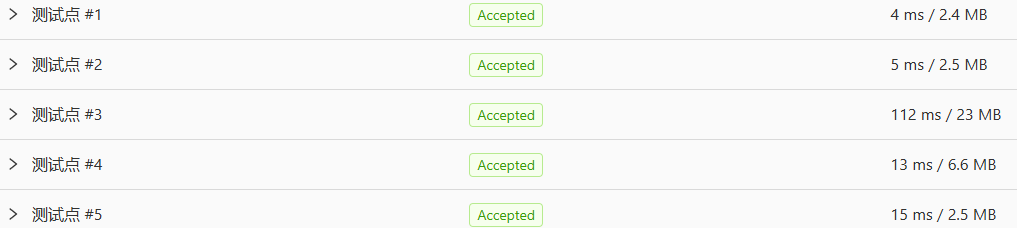
所以这就是 Trie 的强大之处：它能通过把现行的问题转化成树上问题来降低时间复杂度。当然，仅限于关于前缀的问题。

预告： 下一篇文章：《AC 自动机详解》。