KMP 详解-优快云博客

前言

KMP 其实算是字符串中非常难学但又非常有用且凝练的一类知识，难主要是因为它的思想很深邃（甚至引出了 AC 自动机），凝练又主要是因为它的代码很简洁优美，却又不易理解透彻，因此如果有哪里表述不清楚或没讲明白的请多多包涵。

首先在文章开头我将向 Knuth、Pratt 和 Morris 三位老爷子致意，在你学懂 KMP 算法后，你肯定会被三位老爷子的聪明才智所折服。

KMP 算法解决的问题

~~众所周知~~，KMP 算法主要解决的问题就是在一个字符串中找它的子串，或者换一种方式说，就是找字符串 $t$ 在字符串 $s$ 中出现的位置，打个比方，比如说我们现在要在字符串 “teacher” 里找到字符串 “ache”，那很明显，人眼一看就知道它在第三个位置，但问题是计算机它看不到，如何让计算机找到这个位置呢？

第一阶段：暴力枚举

最简单也最直白的方法：暴力枚举。

其实就是在 $s$ 中确定一个点作为起点，看看是否与 $t$ 第一个字母相同，然后往后遍历，看看后面是否全一样，如果全一样那答案就是这，反之就接着找，因为字符串中有重复字母，所以要想完整的找到就必须每个点都作为起点一次，然后每次又要往后遍历，因此总时间复杂度就是 $O (nm)$ 。

很明显，这种方法在 $n$ 和 $m$ 很小的时候还将就能用一下，一旦超过 $10^4$ 就超时。

第二阶段：KMP 算法

时间来到 20 世纪……

由于暴力枚举的的时间复杂度超高，经常导致计算机运行时间太长（我编的），于是 Knuth、Pratt 和 Morris 三人很不甘心啊：凭啥我们的算法就要慢一点呢？三人一拍即合，一通研究后发现一个最重要的问题：不必要的比较太多了！

比如说这样两个字符串：

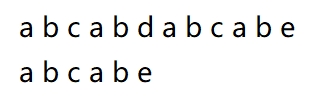
如果是正常的暴力枚举，那在枚举到第二个字符串的最后一个字符的时候就会发现字母不一样了，但是发现这一点后暴力枚举并没有选择跳过中间那一段，而是继续到下一位去枚举。很明显，中间的 “b c” 这一段是肯定不与 “a” 相同的，于是 KMP 就从这里入手，优化了时间。

KMP 的实际做法

首先我们可以看到上面的那两个字符串的前后有一节相同的字母 “a b”，这说明了什么？这说明我们在当前不匹配的情况下可以把前面的那个 “a b” 跟后面的那个 “a b” 对齐再看，也就是这样：

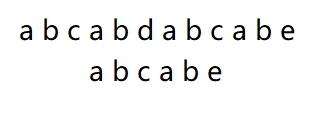
然后重复上述操作就行了。

那我们怎么找到要移动到的位置呢？

通过观察，我们发现一个很重要的数据：最长的前后相同的字符串长度，也就是传说中的最长公共前后缀。 什么意思呢？我们还是拿上面那个例子来看：

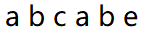
你比如说上面这个字符串，现在我要找一到五位的最长公共前后缀的长度，那是什么呢？我们分开看，首先是“最长”，其次是“公共”，最后就是“前后缀”，也就是前缀和后缀，连在一起就是“最长的前后都有的公共的子串”。那上面那个问题的答案就很容易看出来了：就是 $2$ 。

现在又一个问题来了：怎么求最长公共前后缀的长度？我们先上代码：

void get_next()
{
	int i=0,j=-1;
	nx[0]=-1;
	while(i<n1-1)
	{
		if(j==-1||b[i]==b[j])
		{
			j++,i++;
			nx[i]=j;
		}
		else
		{
			j=nx[j];
		}
	}
}

我来解释一下：

首先我们假定这是一个字符串：

其次找出我们的两个指针 $i$ 和 $j$ ：

然后标出现在的最长公共前后缀：

现在分情况看：

如果 b[i]==b[j] 或者现在在第一个，那么就可以把它加入最长公共前后缀中，这时直接更新（也就是上面的 if）。

如果 b[i]!=b[j]，这说明我们需要把当前的最长公共前后缀变成公共前后缀，而非最长，因为我们定义了红色的两部分是当前的最长公共前后缀，所以最长公共前后缀的最长公共前后缀应该也是一样的，也就是这样：

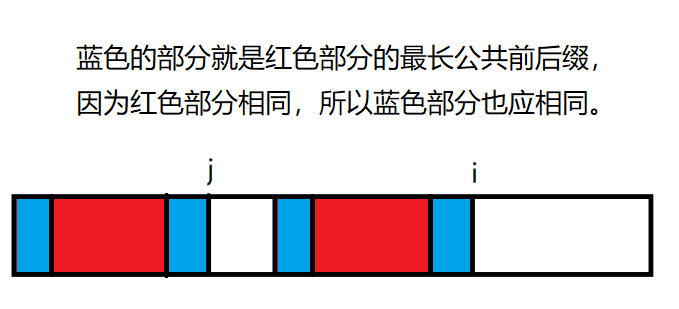
然后我们就把 $j$ 指针给移动了一下：

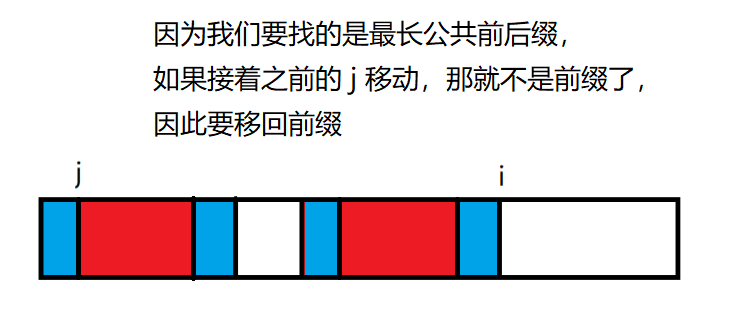
然后重复上述操作。

现在我们再回头看这份代码：

void get_next()
{
	int i=0,j=-1;
	nx[0]=-1;
	while(i<n1-1)
	{
		if(j==-1||b[i]==b[j])
		{
			j++,i++;
			nx[i]=j;
		}
		else
		{
			j=nx[j];
		}
	}
}

是不是感觉清晰多了？

这里注意一下：其实一开始命名这个 nx[0]=-1 是为了方便查找，因为如果我们完全没有最长公共前后缀，那么走着走着就会走到 $0$ 这个位置（可以自己实操一下），如果这时我们还令 nx[0]=0，那就停不下来了，就会一直循环跑。但如果我们把上面的 j==-1 改成 j==0，那就又回出现一个问题：我们知道字符串都是从 $0$ 开始的，所以如果两个字符串的第 $0$ 位不同，但按照这样的判断我们会把它放入最长公共前后缀中，这时就会出错，所以我们定义了一个 nx[0]=-1。

然后我们就来看 KMP 的代码：

int KMP()
{
	get_next();//算出 next 数组
	int i=0,j=0;
	while(i<n1&&j<n2)
	{
		if(j==-1||a[i]==b[j])//如果在开头或者这两位相等，那我们直接往后移动继续判断
		{
			i++,j++;
		}
		else//反之说明有一位不同，那么就移动到当前的最长公共前后缀
		{//因为一段子串的最长公共前后缀是相同的，那我们就可以把这两部分对齐再判断
			j=nx[j];
		}
	}
	if(j>=n2)//如果整个字符串都跑完了，说明 a 中有一段子串是与 b 中完全重合的
	{
		return i-n2+1;//那么输出起点的位置（这个自己想为什么这样算）
	}
	return -1;
}

其实就跟之前我讲的差不多，具体可看注释。

现在我们来算一下时间复杂度：我们设 $s$ 的长度为 $n$ ， $t$ 的长度是 $m$ ，按照之前的算法应该是 $O (nm)$ ，但是按照 KMP 算法，首先找 next 指针是 $O (m)$ 的，其次 KMP 的部分时间复杂度最高是 $O (n)$ 的，所以总时间复杂度就是 $O (n + m)$ ，比之前快了不少！