非线性光学散射偏微分方程组的matlab求解仿真

目录

一、理论基础

二、核心程序

三、测试结果

---

一、理论基础

      非线性光学散射是研究光与物质相互作用的重要手段之一，它可以描述光在物质中的传播、吸收、散射等行为。非线性光学散射的理论基础是量子力学和经典电动力学，而它的数学描述可以使用偏微分方程组来表示。非线性光学散射主要研究的是强相干光（如激光）与物质的相互作用，这种相互作用会导致光的频率、传播方向、偏振状态等特性的变化，以及物质折射率、吸收系数等光学性质的改变。非线性光学散射在激光技术、光谱学和物质结构分析等领域都有着广泛的应用。

       非线性光学散射的基本原理是量子力学和经典电动力学，它涉及到光的波动性和粒子性，以及光与物质的相互作用等过程。非线性光学散射的研究对象是非线性光学材料和介质，这些材料和介质在强光作用下会发生非线性极化，从而产生一系列的光学现象，如倍频、和频、差频、光克尔效应、光散射等。

        非线性光学散射的基本数学描述是偏微分方程组，这些方程组涉及到光的传播、物质的极化、光与物质的相互作用等过程。常用的偏微分方程组包括耦合波方程、非线性薛定谔方程、广义费米-狄拉克方程等。这些方程组通常需要使用数值方法和计算机模拟来求解，以获得光在物质中的传播规律和光学性质的定量描述。

       非线性光学散射在激光技术中有着广泛的应用，例如激光器设计、光学滤波器、光学放大器等领域。同时，非线性光学散射也是光谱学和物质结构分析的重要手段之一，它可以提供物质内部结构和化学反应过程的详细信息。此外，非线性光学散射在医学、通信、能源等领域也有着广泛的应用。非线性光学散射偏微分方程组描述了光与物质的相互作用以及光在物质中的传播，它的基本原理是：光在物质中传播时，会与物质分子或原子相互作用，这种相互作用会导致光的散射和吸收等行为，同时也会引起光强的衰减和相位的变化。
       非线性光学散射偏微分方程组的基本形式是一组耦合的偏微分方程，其中包含了一个或多个偏微分方程，这些方程描述了光在物质中的传播和散射等行为。这个偏微分方程组可以用来描述非线性光学散射的基本现象，例如光的传播、吸收、散射等行为。通过求解这个偏微分方程组，可以得到光在物质中的传播规律以及光的散射和吸收等行为。

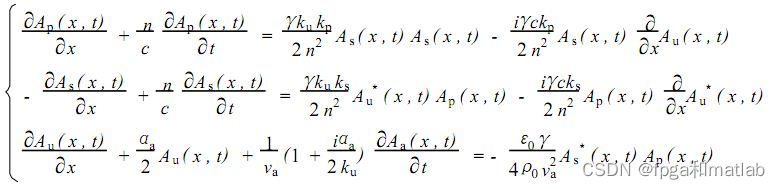
边值条件：

 条件：

       Ap、As、Au都表示瞬时幅度，c=3*10^8，ε0=8.85*10^-12，ρ0=2500，n0=1.0003，n=1.46， va=5980，αa=0.2/4.343*10^-3，γ=(n*n-1)*(n*n+2)/3，ks=kp=5.92*10^6，ka=ku=1.18*10^7，Ip=2*10^15，Is=100，L是x的空间长度人为设定为1厘米，时间长度t人为设定为1毫秒。方程里i是虚数单位，方程里*是共轭，x表示空间一维，t表示时间维，第三个方程里Aa应该是Au。有需要再补充

要求：

       程序里需要n、L、t、αa 、Ip 、Is 、ks、kp、ka等基本常数都可以灵活微调（就是说作为全局变量的意思吧）；用常用算法比如有限差分法解方程组。

     P，S，U三个光P和U是同方向传播的，S为反方向传播，那么差分方程如下所示：

 ★化简得到如下的式子：

 ★进一步简化得到：

     显然，上面的公式是一组隐性的差分方程组，因此，我们需要做近似，然后再做迭代进行处理，近似做法如下所示。 

根据上面最后一个公式进行编程。

二、核心程序

.............................................................
%%
%利用有限差分法将偏微分方程转换为差分方程形式
K11 =  1 + (dx*n)/(dt*c);
K12 = -1;
K13 = (dx*n)/(dt*c);
K14 = (dx*r*ku*kp)/(2*n*n);
K15 = -1*i*(r*c*kp)/(2*n*n);

K21 = -1 + (dx*n)/(dt*c);
K22 =  1;
K23 = (dx*n)/(dt*c);
K24 = (dx*r*ku*ks)/(2*n*n);
K25 = -1*i*(r*c*kp)/(2*n*n);

K31 = -1 + (aa*dx)/2 + dx*(1+i*aa/ku)/(va*dt);
K32 =  1;
K33 =  dx*(1+i*aa/ku)/(va*dt);
K34 = -1*(dx*e0*r)/(4*p0*va*va);
 

%%Ap(Lx,Tx+1)   = (-K12*Ap(Lx-1,Tx+1) + K13*Ap(Lx,Tx) + K14*As(Lx,Tx+1)*As(Lx,Tx+1) + K15*As(Lx,Tx+1)*(Au(Lx,Tx+1)-Au(Lx-1,Tx+1)))/K11;
%Ap(Lx,Tx+1)    = (-K12*Ap(Lx-2,Tx)   + K13*Ap(Lx,Tx) + K14*As(Lx-1,Tx)*As(Lx-1,Tx) + K15*As(Lx-1,Tx)*(Au(Lx-1,Tx)-Au(Lx-2,Tx)))/K11;

%Lx2            = L-Lx;
%%As(L-Lx,Tx+1) = (-K22*As(L-Lx+1,Tx+1) + K23*As(L-Lx,Tx) + K24*conj(Au(L-Lx,Tx+1))*Ap(L-Lx,Tx+1) + K25*Ap(L-Lx,Tx+1)*(conj(Au(L-Lx,Tx+1))-conj(Au(L-Lx-1,Tx+1))))/K21;
%As(Lx2,Tx+1)   = (-K22*As(Lx2+2,Tx)    + K23*As(Lx2,Tx)  + K24*conj(Au(Lx2+1,Tx)) *Ap(Lx2+1,Tx)    + K25*Ap(Lx2+1,Tx)*(conj(Au(Lx2+1,Tx))-conj(Au(Lx2,Tx))))/K21;


%%Au(Lx,Tx+1)   = (-K32*Au(Lx-1,Tx+1) + K33*Au(Lx,Tx) + K34*conj(As(Lx,Tx+1))*Ap(Lx,Tx+1))/K31;
%Au(Lx,Tx+1)   = (-K32*Au(Lx-2,Tx)    + K33*Au(Lx,Tx) + K34*conj(As(Lx-1,Tx))*Ap(Lx-1,Tx))/K31;

Ap(1,1) = sqrt(2*Ip/c/n0/e0);
As(L,1) = sqrt(2*Is/c/n0/e0);
Au(1,1) = 0;  

%下面使用差分迭代的方法来对三个变量进行求解
for Lx = 3:L-3%距离微分 
    ttt = 0;
    for Tx = 1:T-1%时间微分
        fprintf('距离微分:');
        fprintf('%2.4f  |  ',Lx);
        fprintf('时间微分:');
        fprintf('%2.4f',Tx);
        fprintf('\n');
        Lx2            =  L-Lx;
        
        Ap(Lx,Tx+1)    = (-K12*Ap(Lx-2,Tx)     + K13*Ap(Lx,Tx)   + K14*As(Lx+1,Tx)*As(Lx+1,Tx)           + K15*As(Lx-1,Tx)*(Au(Lx-1,Tx)-Au(Lx-2,Tx)))/K11;
        
        As(Lx2,Tx+1)   = (-K22*As(Lx2+2,Tx)    + K23*As(Lx2,Tx)  + K24*conj(Au(Lx2+1,Tx)) *Ap(Lx2+1,Tx)  + K25*Ap(Lx2+1,Tx)*(conj(Au(Lx2+1,Tx))-conj(Au(Lx2,Tx))))/K21;
        
        Au(Lx,Tx+1)    = (-K32*Au(Lx-2,Tx)     + K33*Au(Lx,Tx)   + K34*conj(As(Lx-1,Tx))*Ap(Lx-1,Tx))/K31;    
    end 
    Ap(Lx ,:) = Ap(Lx ,:)/1e2;
    As(Lx2,:) = As(Lx2,:);
    Au(Lx ,:) = Au(Lx ,:)/1e2;
end
.........................................................................

三、测试结果

    这里，通过以动态效果进行仿真，从而直接给出同时反映波空间和时间的二维动态效果图。当波接触的时候，会产生相互的影响。具体见仿真结果。

  

 A16-18