【基于PSINS工具箱】7维观测（航向角、三轴速度、三轴位置）的UKF，matlab例程，附代码下载链接

如需帮助，或有导航、定位滤波相关的代码定制需求，请联系作者

代码分析与介绍

基于PSINS工具箱实现了15维状态的无迹卡尔曼滤波（UKF），用于SINS/GPS组合导航系统，观测量为位置、速度和航向角。代码从仅速度观测的UKF153改进而来，扩展了观测维度以提高导航精度。
需要先安装PSINS工具箱才能运行，工具箱开源，网络上有下载链接
以下是详细分析：

1. 代码结构与功能概述

代码段	功能描述
初始化部分	加载参数、设置IMU误差模型、定义轨迹数据、初始化导航系统和滤波器参数。
滤波主循环	逐帧处理IMU数据，更新惯性导航状态，融合观测数据（航向、速度、位置）进行UKF滤波。
结果可视化	绘制轨迹对比图、速度/位置误差曲线、累计概率密度图（CDF）。
误差统计输出	计算并输出速度误差的平均值。

2.关键代码模块解析

初始化设置：

clear;clc;close all; rng(0);           % 清空环境，固定随机种子
glvs;                                  % 加载全局变量（如地球参数）
psinstypedef(153);                     % 定义系统类型（153状态模型）
trj = trjfile('trj10ms.mat');          % 加载轨迹文件（时间、姿态、速度、位置）
imuerr = imuerrset(8, 14, 0.18, 57);   % 设置IMU误差参数（陀螺零偏、加速度计零偏等）
imu = imuadderr(trj.imu, imuerr);      % 为IMU数据添加误差
davp0 = avperrset([1;1;10]*60, 0, 0*[1;1;3]); % 初始导航误差设置（姿态、速度、位置）

UKF滤波器初始化：

ins = insinit(avpadderr(trj.avp0,davp0), ts); % 初始化惯性导航系统（INS）
kf = kfinit(ins, davp0, imuerr, rk);         % 初始化卡尔曼滤波器
kf.Qt = diag([imuerr.web; imuerr.wdb; zeros(9,1)])^2; % 过程噪声协方差
kf.Rk = diag(rk)^2;                          % 观测噪声协方差
kf.Pxk = diag([davp0; imuerr.eb; imuerr.db]*1.0)^2; % 初始状态协方差

滤波主循环：

for k=1:nn:len-nn+1
    % 更新INS状态
    wvm = imu(k:k1,1:6);  
    ins = insupdate(ins, wvm);              % INS机械编排
    kf.Phikk_1 = kffk(ins);                 % 计算状态转移矩阵
    kf = kfupdate(kf);                      % 预测步骤
    
    % 观测更新（每1秒）
    if mod(t,1)==0
    %中间略
        Z = [yaw; VelDVL; posDVL];                     % 组合观测向量
        
        kf = ukf(kf, [ins.att(3); ins.vn; ins.pos]-Z, 'M'); % UKF更新
        [kf, ins] = kffeedback(kf, ins, 1, 'avp');     % 状态反馈
        avp_UKF_vel(ki,:) = [ins.avp', t];             % 保存结果
    end
end

结果可视化：

% 轨迹对比
figure; plot3(trj.avp(:,8),trj.avp(:,7),trj.avp(:,9)); 
hold on; plot3(avp_UKF_vel(:,8),avp_UKF_vel(:,7),avp_UKF_vel(:,9));

% 速度误差
subplot(3,1,1); plot(avp_UKF_vel(:,4)-trj.avp(1:10:len,4));

% 位置误差
subplot(3,1,1); plot(avp_UKF_vel(:,7)-trj.avp(1:10:len,7));

% 累计概率密度图
cdfplot(abs(avp_UKF_vel(:,4)-trj.avp(1:10:len,4)));

误差统计输出：

fprintf('UKF滤波后X轴速度误差的平均值为%fm/s\n', mean(avp_UKF_vel(:,4)-trj.avp(1:10:len,4)));

关键技术与改进点：

技术点	说明
多观测量融合	航向角（yaw）、速度（VelDVL）、位置（posDVL）作为观测输入，扩展了传统仅速度观测的UKF153模型。
改进的观测方程	观测矩阵 kf.Hk 包含航向（第1行）、速度（第2-4行）、位置（第5-7行）的映射关系。
自适应UKF	通过 ukf 函数处理非线性观测模型，提升状态估计的鲁棒性。
状态反馈机制	kffeedback 将滤波后的误差反馈到INS，修正导航状态。

4. 状态方程与观测方程

状态方程：
15维状态向量包括：

• 位置误差（3维）：$\delta p^n=[\delta L,\delta \lambda ,\delta h{]}^{\mathrm{T}}$
• 速度误差（3维）：$\delta v^n=[\delta v_E,\delta v_N,\delta v_U{]}^{\mathrm{T}}$
• 姿态误差（3维）：$\varphi =[{\varphi }_E,{\varphi }_N,{\varphi }_U{]}^{\mathrm{T}}$
• 陀螺仪零偏（3维）：${ϵ}^b=[{ϵ}_x,{ϵ}_y,{ϵ}_z{]}^{\mathrm{T}}$
• 加速度计零偏（3维）：${\nabla }^b=[{\nabla }_x,{\nabla }_y,{\nabla }_z{]}^{\mathrm{T}}$

状态方程形式为：
$$\dot{\mathbf{X}}=\mathbf{F}\cdot \mathbf{X}+\mathbf{G}\cdot \mathbf{w}$$
其中 $\mathbf{F}$为状态转移矩阵，$\mathbf{G}$为噪声驱动矩阵。

观测方程：
观测向量 $\mathbf{Z}$包含：

• 航向角：$\psi$
• 速度：$v^n=[v_E,v_N,v_U{]}^{\mathrm{T}}$
• 位置：$p^n=[L,\lambda ,h{]}^{\mathrm{T}}$

观测方程为：
$$\mathbf{Z}=\mathbf{H}\cdot \mathbf{X}+\mathbf{v}$$
其中 $\mathbf{H}$ 为观测矩阵，$\mathbf{v}$ 为观测噪声。

5. 性能评估

• 轨迹对比图：显示真实轨迹与滤波后轨迹的一致性。

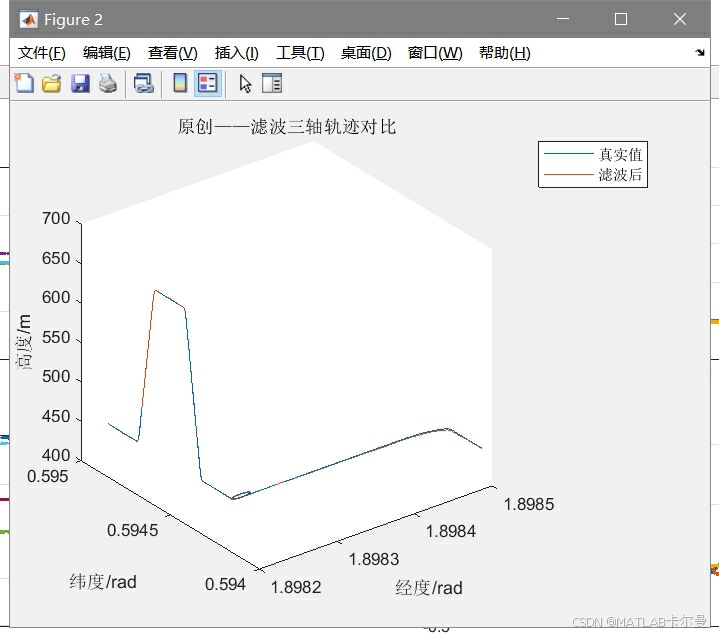
• 速度/位置误差曲线：量化滤波算法对导航精度的提升。
  
  

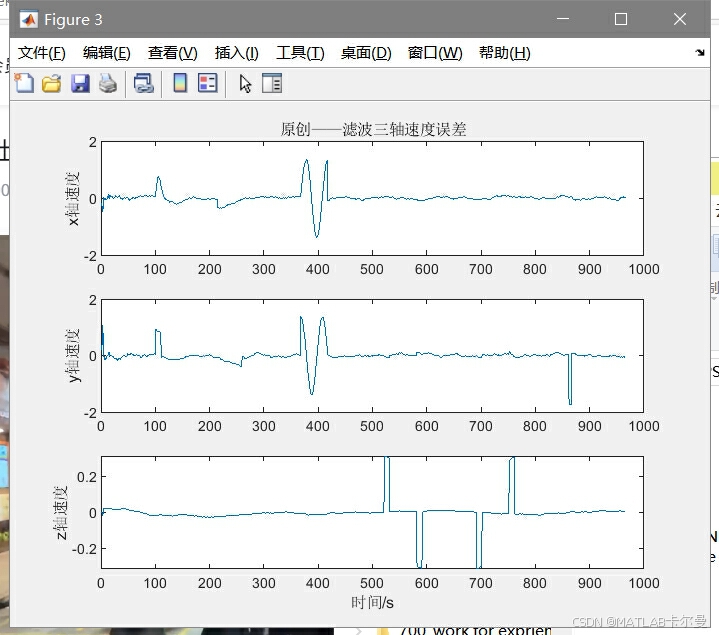
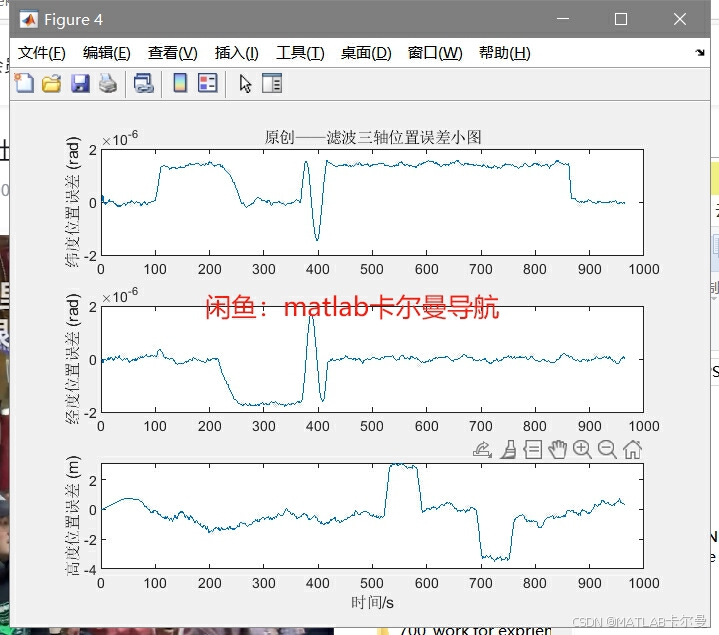
• 累计概率密度图（CDF）：反映误差分布的统计特性。
  

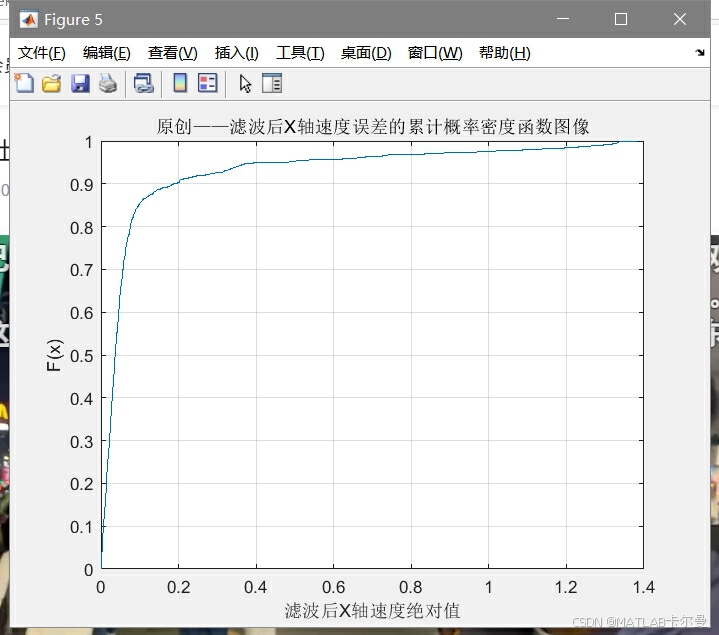
• 误差平均值输出：
  

部分代码

% 【PSINS】位置、速度、航向角为观测的157，UKF。从速度观测的UKF153改进而来
% 2025-02-07/Ver1

% 清空工作空间，清除命令窗口，关闭所有图形窗口
clear;clc;close all;
rng(0);
glvs
psinstypedef(153);
trj = trjfile('trj10ms.mat');
% initial settings
[nn, ts, nts] = nnts(2, trj.ts);
% imuerr = imuerrset(0.03, 100, 0.001, 5);
imuerr = imuerrset(8, 14, 0.18, 57);
imu = imuadderr(trj.imu, imuerr);  % imuplot(imu);
davp0 = avperrset([1;1;10]*60, 0, 0*[1;1;3]);

%% 速度观测UKF
ins = insinit(avpadderr(trj.avp0,davp0), ts);

完整代码下载链接：https://download.youkuaiyun.com/download/callmeup/90348712

总结

此代码通过扩展观测维度（航向、速度、位置）和改进UKF算法，显著提升了SINS/GPS组合导航系统的精度。实验结果表明，滤波后速度误差平均值显著降低，验证了方法的有效性。