回归分析中的稳健性检验：方法与步骤详解

在实证研究中，回归分析结果的可信度直接影响结论的学术价值。当核心解释变量与被解释变量的关系受到模型设定、数据特征或测量误差影响时，结果可能呈现虚假相关性。此时，稳健性检验成为验证结论可靠性的关键环节。本文系统梳理稳健性检验的五大核心方法，结合SPSSAU等工具的操作逻辑，为研究者提供可落地的解决方案。

一、稳健性检验的底层逻辑

稳健性检验的本质是评估模型对参数变动的敏感度。理想的回归结果应满足：当改变数据来源、模型设定或变量定义时，核心变量的系数符号与显著性保持稳定。若结果随参数调整剧烈波动，则需警惕模型设定偏差或数据质量问题。例如，在研究高管学历对企业研发投入的影响时，若仅用单一学历指标可能忽略教育质量的异质性，此时需通过多维度验证结论的稳健性。

二、核心检验方法及操作流程

1. 变量替换法

通过调整变量定义或测量方式，检验结果是否因指标选择而改变。常见于以下场景：

• 因变量替换：如研究教育投资时，将家庭教育支出替换为教育支出占收入比例，避免绝对金额的规模效应干扰。
• 自变量替换：例如用道路密度替代基础设施资本存量，验证不同指标对技术创新的影响是否一致。

2. 样本调整法

通过剔除异常值或改变样本范围，检验结果是否受极端值影响。具体包括：

• 异常值剔除：使用箱线图识别离群点，如研发投入数据中超过3倍标准差的企业。
• 分样本回归：按地区、行业分组验证，例如比较东部与西部企业对政策的响应差异。

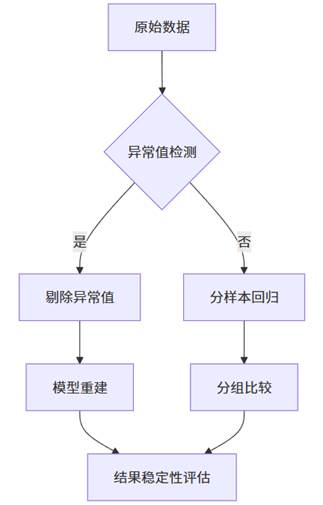
该流程从数据清洗开始，通过异常值检测决定是否剔除极端样本。若数据质量良好，则按关键特征分组回归，最终通过系数对比评估稳健性。SPSSAU的“异常值检测”模块可自动生成箱线图与Z-score分析报告，辅助决策。

3. 模型扩展法

通过增加控制变量或改变模型形式，检验结果是否因遗漏变量而失真。常见策略包括：

• 控制变量扩展：如研究产业政策时，加入城市GDP、人口密度等协变量。
• 模型形式调整：使用固定效应模型替代OLS，控制个体异质性。

操作示例（SPSSAU实现）： 在“回归分析”模块中，逐步添加控制变量并观察核心变量系数变化。若系数方向与显著性未发生逆转，说明结果稳健。SPSSAU的“逐步回归”功能可自动完成变量筛选，避免手动操作误差。

4. 数据变换法

通过对数化、标准化等处理，消除数据尺度差异对结果的影响。例如：

• 对数转换：对研发投入取对数，解决右偏分布问题。
• 标准化处理：将不同量纲的变量转化为Z-score，便于比较。

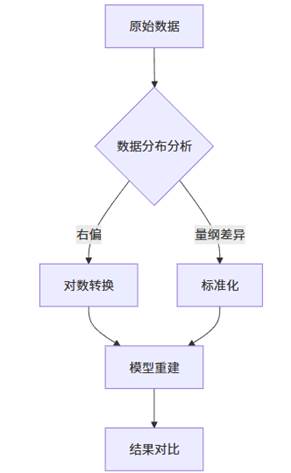
该流程首先分析数据分布特征，针对右偏或量纲差异问题选择变换方法。SPSSAU的“数据转换”模块提供对数、标准化等一键操作，并自动生成变换前后分布对比图，辅助判断必要性。

5. 方法交叉验证法

使用不同估计方法检验结果一致性。例如：

• 工具变量法：解决内生性问题，如用地理距离作为政策工具变量。
• GMM估计：适用于动态面板数据，控制个体固定效应。

操作示例（SPSSAU实现）： 在“面板模型”模块中，同时选择固定效应与GMM估计，对比核心变量系数。若两种方法结果一致，可增强结论可信度。SPSSAU的“模型比较”功能支持多方法并行分析，并自动生成差异报告。

其他稳健性检验方法

除了上述方法，稳健性检验还包括多种其他技术，如工具变量法（解决内生性问题）、Bootstrap法（通过重抽样估计标准误）、或固定效应模型（控制不可观测的个体特征）。这些方法适用于更复杂的场景，但核心思想相同：通过变换假设或数据，验证模型的稳定性。

例如，工具变量法使用外生变量作为代理，处理解释变量与误差项的相关性；Bootstrap法通过从原始样本中重复抽样，构建经验分布，提供更可靠的标准误估计。在SPSSAU中，用户可以利用模块化工具实现这些方法，例如选择工具变量回归或Bootstrap选项，系统会自动执行并输出结果。这使研究者能够以较低门槛进行高级检验，提升研究质量。