分层回归中如何判断调节效应是否显著？一套清晰的三步判断法则

在社会科学、管理学及心理学等领域的实证研究中，我们常常不满足于仅仅了解变量间的直接关系。一个更具深度的问题是：两个变量之间的关系，是否会因为第三个变量的不同而发生变化？ 例如，“工作投入”（X）对“工作绩效”（Y）的促进作用，在“领导支持”（Z）高的员工中是否更强？这种“它如何改变它”的问题，就是调节效应 研究的核心。

分层回归，作为一种强大且灵活的统计工具，为我们提供了检验调节效应的经典路径。与专门化的“调节作用”分析模块相比，分层回归通过构建一系列嵌套模型，像剥洋葱一样，层层深入地揭示变量间的作用机制。本文将系统阐述如何通过分层回归模型，严谨地判断调节效应是否显著，并解析其中的关键指标与理论逻辑。

一、理论先行：什么是调节效应？

在展开分析之前，我们必须从理论上明确调节效应的概念。如果一个变量 Z 能够改变自变量 X 与因变量 Y 之间关系的强度或方向，那么 Z 就被称为调节变量。

在统计上，调节效应主要通过 X 与 Z 的交互项（X × Z） 来体现。如果这个交互项的回归系数是显著的，则说明调节效应存在。这意味着，X 对 Y 的影响大小，依赖于 Z 的具体取值。

分层回归的思路，正是通过逐步引入变量，来检验这个交互项的“贡献”是否足够显著。

为了全局把握整个分析流程，我们首先通过下面的流程图来一览全貌：

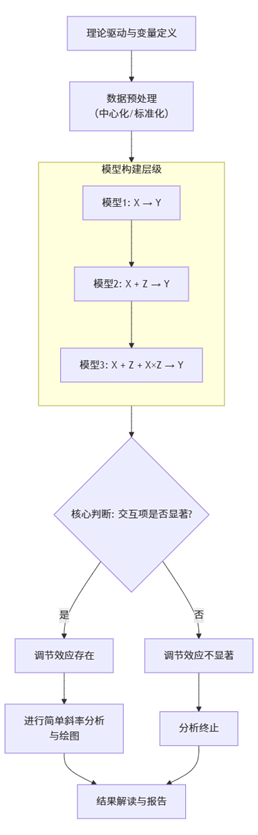
如上图所示，一个严谨的调节效应检验始于理论假设，历经关键的数据预处理和模型构建阶段，最终通过检验交互项的显著性来做出统计决策。如果效应存在，还需进行深入的后置分析以明确其具体形态。这是一个环环相扣的逻辑链条。

二、核心步骤一：不可或缺的数据预处理

在构建交互项之前，一项至关重要却常被忽视的步骤是对自变量 X 和调节变量 Z 进行中心化或标准化处理。为何要处理？

（1）降低多重共线性：未经处理的 X 和 Z 通常与它们的交互项（X × Z）高度相关，这会引发严重的多重共线性问题，导致模型估计不稳定，标准误膨胀，使得本应显著的效应变得不显著。中心化处理能有效减弱这种相关关系。

（2）提升系数可解释性：中心化后，变量的均值变为0。此时，模型中 X 的系数（即直接效应或主效应）被解释为“当 Z 处于其平均水平时，X 对 Y 的影响”。这比解释“当 Z=0 时”更具现实意义。

（3）SPSSAU的便捷实现：
在SPSSAU的【数据处理】->【生成变量】，选中变量进行中心化或标准化处理。

三、核心步骤二：构建三层级回归模型

分层回归的精髓在于模型的逐层构建。我们通常需要建立三个模型：

• 模型一（基准模型）：仅包含自变量 X。
  Y = β₀ + β₁X + e
  此模型旨在考察 X 对 Y 的总主效应，为后续模型提供一个比较的基准。
• 模型二（主效应模型）：在模型一的基础上，加入调节变量 Z。
  Y = β₀ + β₁X + β₂Z + e
  此模型同时考察 X 和 Z 对 Y 的主效应。此时，我们关注的是在控制 Z 的影响后，X 的效应是否依然稳定。
• 模型三（全模型/调节效应模型）：在模型二的基础上，加入核心的交互项 X × Z。
  Y = β₀ + β₁X + β₂Z + β₃(X × Z) + e
  这是我们检验调节效应的核心模型。所有的秘密都藏在系数 β₃ 之中。

SPSSAU使用分层回归进行调节效应分析操作示例如下：

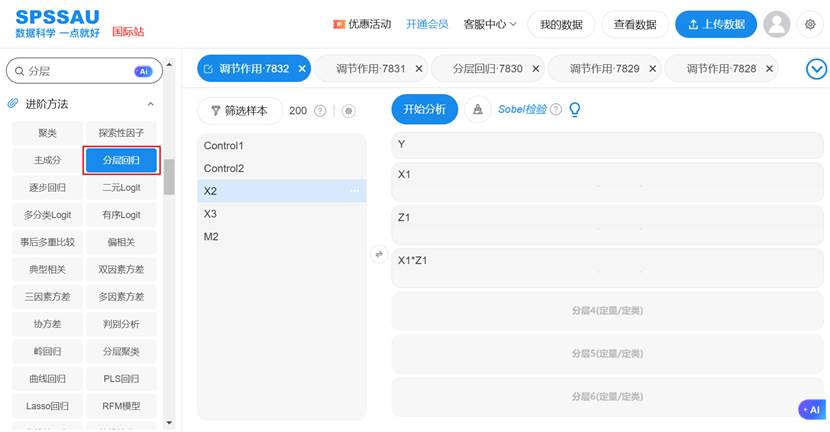
SPSSAU输出分层回归结果示例如下：

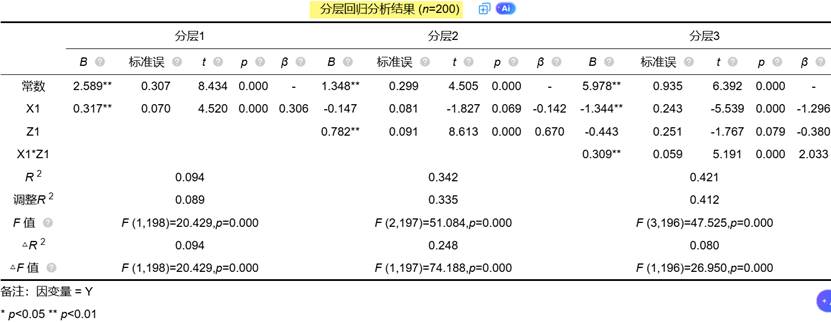
四、核心步骤三：判断调节效应显著性的双重准则

如何基于上述三个模型，做出调节效应是否显著的判断？我们有两个相互印证的标准：

准则一（核心准则）：交互项系数的显著性

这是最直接、最关键的判断依据。在模型三中，我们直接检查交互项（X × Z）的回归系数（β₃）是否显著。

• 如何判断：查看交互项系数对应的 *p* 值。如果 *p* < 0.05（或 0.01），则认为该交互项系数显著不为零。
• 理论意义：系数显著意味着 X 对 Y 的影响程度，确实会随着 Z 的变化而产生有规律的变化。调节效应成立！

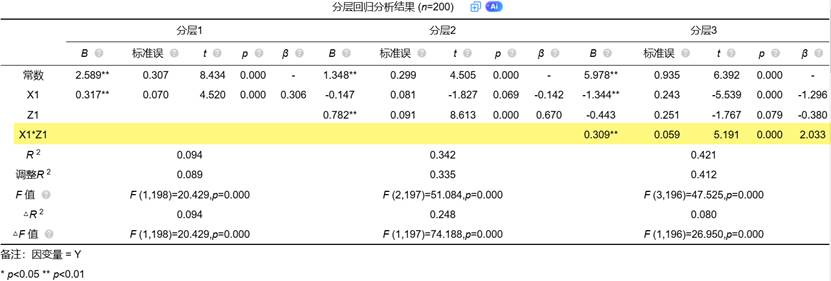
准则二（辅助准则）：模型解释力的显著提升——ΔR²

这个准则从模型整体拟合优度的角度提供佐证。它回答的问题是：“加入交互项后，模型对因变量 Y 的解释力是否获得了统计学上的显著提升？”

（1）如何判断：关注从模型二到模型三的 △R²（R方变化量）及其对应的 △F 检验。

△R²：代表了交互项独自为模型带来的“新增解释力”。

△F 检验：如果这个变化的 *p* 值显著（< 0.05），则说明 △R² 的提升是真实的，不是由抽样误差导致的。

（2）理论意义：一个显著的 △F 检验，从模型整体比较的角度，证实了引入交互项是必要且有价值的，它确实提供了新的信息。

通常情况下，准则一和准则二的结论是一致的：即交互项显著，同时 △R² 也显著。此时，我们可以非常自信地得出结论：调节效应存在。

五、一个重要的诊断：警惕多重共线性

在解读模型三时，有一个“陷阱”需要警惕。由于引入了交互项，即使进行了中心化，方差膨胀因子（VIF） 也可能较高。VIF是衡量多重共线性严重程度的指标。

• 理论意义：通常认为 VIF < 10（更严格的标准是 5）时，多重共线性在可接受范围内。如果 VIF 值过高，虽然不会影响模型整体的预测能力，但会使得各个自变量的回归系数估计不稳定，难以准确解释每个变量的独立贡献。
• SPSSAU的辅助功能：SPSSAU的分层回归输出结果中，会自动提供每个模型中各个变量的 VIF 值，帮助您进行诊断。在调节效应分析中，交互项的 VIF 较高是一个常见现象，关键在于理解其含义，并优先依赖整体模型的显著性判断。

六、效应成立之后：简单斜率分析与可视化

当确认调节效应显著后，我们的工作并未结束。一个完整的分析还必须回答：“调节的具体模式是什么？”也就是说，我们需要知道在调节变量 Z 的不同水平上，X 对 Y 的影响（即斜率）具体是怎样的。

这就是简单斜率分析。我们通常会计算在 Z 处于“高水平”（如均值加一个标准差）、“平均水平”（均值）和“低水平”（均值减一个标准差）时，X 对 Y 的回归斜率，并检验这些斜率是否显著。

最直观的展示方式则是绘制简单斜率图，它将不同 Z 水平下 X 与 Y 的关系用直线表示出来，几条直线的斜率差异一目了然。

更优的解决方案是：直接使用SPSSAU的【问卷研究】→【调节作用】分析模块。

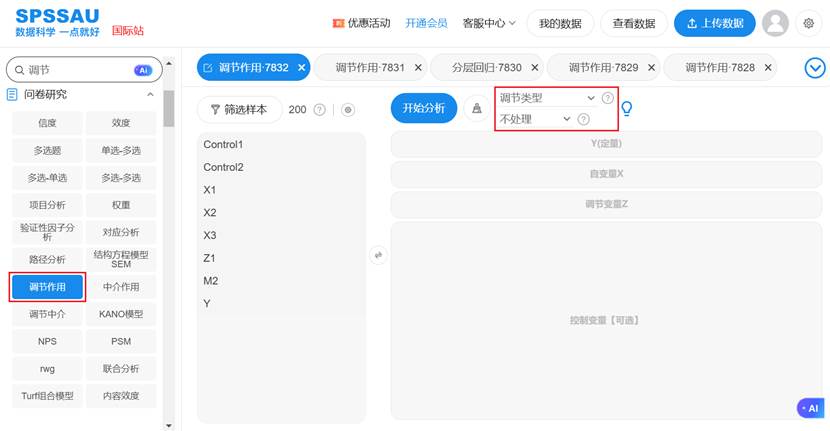
该功能是专门为调节效应分析量身定制的。它自动完成了从中心化、生成交互项、到分层回归检验、输出智能解读、乃至自动生成简单斜率图的全过程。您只需要拖拽变量，选择类型，系统便会一键生成所有结果和图表，极大地提升了分析效率和准确性，让研究者可以更专注于理论阐释而非技术细节。

无论您选择经典的分层回归路径，还是更高效的专用调节作用分析，掌握其背后的统计原理，都是做出严谨、可信的研究结论的基石。