回归模型的拟合优度到底怎么判断？一次讲清所有关键指标

最新推荐文章于 2025-12-19 15:31:04 发布

原创最新推荐文章于 2025-12-19 15:31:04 发布 · 671 阅读

CC 4.0 BY-SA版权

文章标签：

在数据分析和机器学习领域，回归模型是最常用且重要的建模技术之一。无论从事市场研究、经济预测还是科学实验，我们常常需要建立回归模型来探索变量之间的关系。但一个关键问题随之而来：如何判断我们建立的回归模型是否“好”？如何评估模型的拟合优度？

本文将系统介绍回归模型拟合优度的评价体系，带你从多个维度全面评估模型质量，避免陷入单一指标评价的误区。

一、什么是模型拟合优度？

模型拟合优度（Goodness of Fit）是指回归模型对观测数据的解释能力，反映了模型预测值与实际值之间的接近程度。一个具有高拟合优度的模型能够更好地捕捉数据中的内在规律，从而提高预测的准确性。

需要注意的是，高拟合优度并不总是意味着模型更好——有时这可能意味着模型过度拟合了训练数据中的噪声，导致在新数据上表现不佳。因此，我们需要一套完整的评估体系来判断模型的真实表现。

二、回归模型评价指标体系

1. 基础拟合优度指标

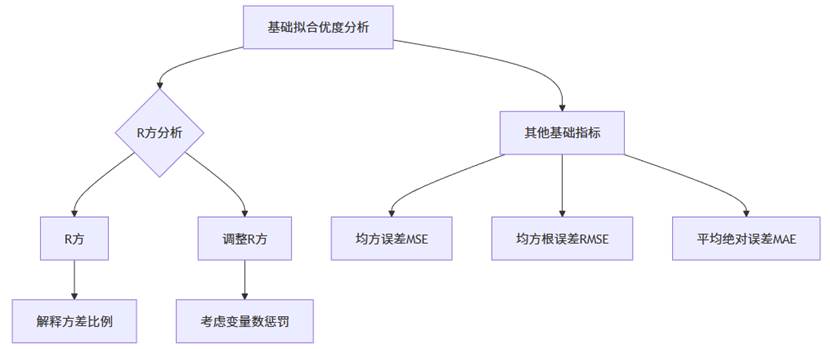
以上流程图展示了基础拟合优度分析的主要路径。在实际分析中，我们通常从R方系列指标入手，了解模型对数据变异的解释能力，然后结合误差指标评估预测精度。

（1）R²（R平方）

R平方是最常用的拟合优度指标，表示模型能够解释的因变量变异性的比例。计算公式为：R² = 1 - SSR/SST

其中SSR是残差平方和，SST是总平方和。R²的取值范围在0到1之间，值越接近1，表示模型对数据的拟合程度越好。

但R²有个重要缺陷：随着自变量数量的增加，R²会持续增大，即使新加入的变量与因变量无关。这可能导致过度拟合的风险。

（2）调整R²（Adjusted R²）

为了解决R²随自变量增加而增大的问题，调整R²引入了自变量个数（p）和样本量（n）的惩罚项：

调整R² = 1 - [(1-R²)(n-1)/(n-p-1)]

当加入无意义的自变量时，调整R²可能会减小，这帮助我们筛选更简洁的模型。在多元回归中，调整R²通常比普通R²更具参考价值。

（3）误差指标

均方误差（MSE） 衡量预测值与实际值之间差异的平方的平均值，对异常值较为敏感：MSE = Σ(预测值-实际值)² / n
均方根误差（RMSE） 是MSE的平方根，与因变量有相同的量纲，更易于解释：
RMSE = √MSE
平均绝对误差（MAE） 衡量预测值与实际值之间绝对差异的平均值，对异常值不那么敏感：MAE = Σ|预测值-实际值| / n

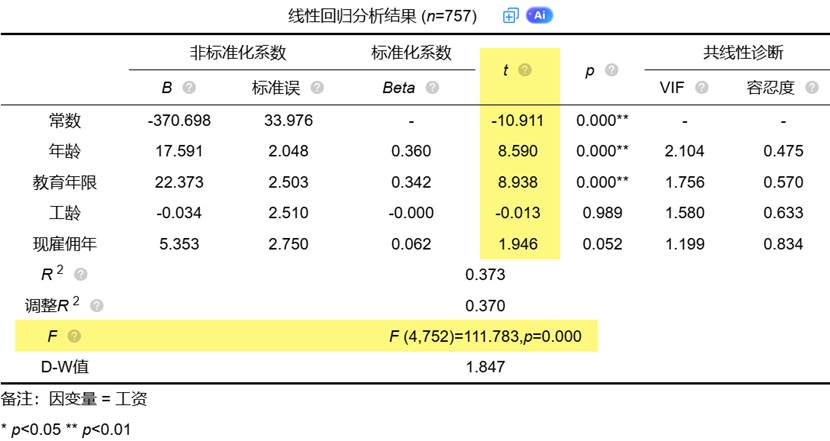
在实际应用中，如SPSSAU等统计分析工具会同时提供这些指标，方便用户从不同角度评估模型精度。这些工具的一键输出功能大大简化了计算过程，让研究者能更专注于结果解释。例如SPSSAU线性回归输出部分指标如下：

2. 统计显著性检验

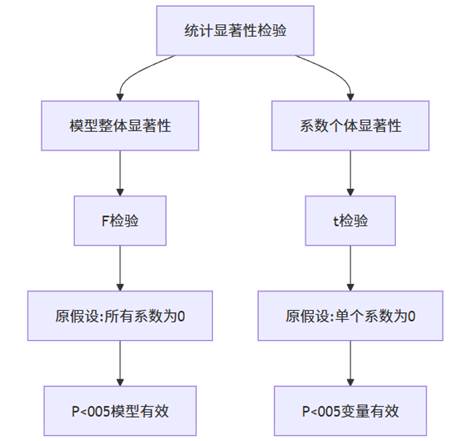
统计显著性检验流程揭示了回归分析中假设检验的双层结构：首先要判断模型整体是否有效，然后检验各个自变量的贡献是否显著。这一流程保证了模型和变量的统计可靠性。

（1）F检验（模型整体显著性检验）

F检验用于检验回归模型整体的显著性，原假设是所有自变量的系数都为0。如果F检验的p值小于显著性水平（通常为0.05），我们拒绝原假设，认为模型整体是显著的，即至少有一个自变量能够有效解释因变量的变异。

（2）t检验（系数显著性检验）

t检验针对每个自变量的回归系数进行，原假设是特定自变量的系数为0。如果t检验的p值小于显著性水平，我们拒绝原假设，认为该自变量对因变量有显著影响。

在实际研究中，我们不仅要关注p值是否小于0.05，还应关注置信区间，它提供了系数估计的不确定性范围。

3. 残差分析

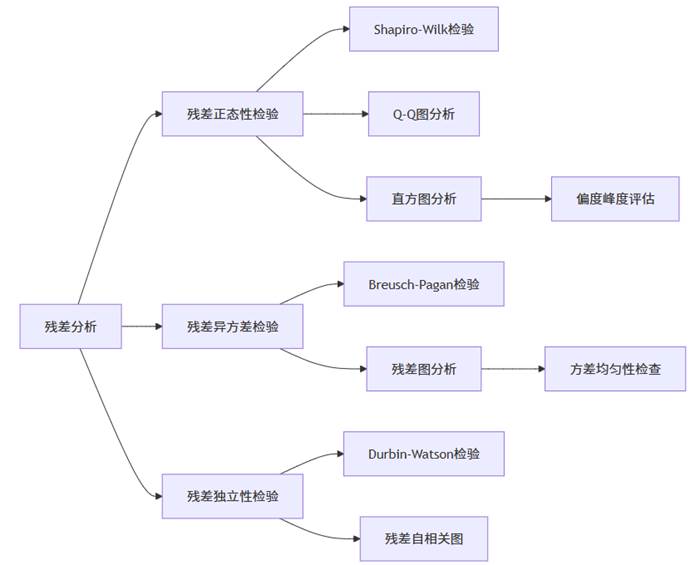
残差分析流程图展示了评估回归模型假设的核心检查点。正态性、同方差性和独立性是回归模型的三大基本假设，只有这些条件得到满足，模型结果的可靠性才有保障。

残差分析是检查回归模型假设是否满足的重要方法。残差是实际值与预测值之间的差异：e = y - ŷ

（1）残差正态性检验：回归模型假设误差项服从正态分布。我们可以通过Shapiro-Wilk检验、Q-Q图或直方图来检验残差的正态性。如果残差严重偏离正态分布，可能会影响假设检验的有效性。

（2）异方差检验：回归模型假设误差项具有常数方差（同方差性）。如果误差方差随着预测值的变化而变化，就存在异方差性，这会影响模型效率。Breusch-Pagan检验或White检验可以检测异方差性，也可以通过残差图直观判断。

（3）独立性检验：回归模型假设误差项相互独立。对于时间序列数据，误差可能存在自相关，这时可以使用Durbin-Watson检验来检测。D-W统计量接近2表示无自相关，显著偏离2则表明存在自相关。

当面对复杂的残差分析时，现代数据分析平台如SPSSAU提供了自动化检验功能，能够一键生成所有必要的检验结果和可视化图形，极大提高了分析效率。

4. 模型诊断与比较

（1）离群点和强影响点检测

离群点（Outliers）是指与大多数数据点明显不同的观测值，可能对回归结果产生不成比例的影响。我们可以通过学生化残差来识别离群点，通常认为绝对值大于2或3的残差对应的点可能是离群点。

强影响点（Influential Points）是指对回归系数估计有显著影响的点。常用的检测指标包括：

杠杆值（Leverage）：衡量观测点与自变量中心的距离
Cook距离：综合衡量一个观测点对所有回归系数的影响程度
DFFITS：衡量删除一个观测点后预测值的变化

（2）模型比较指标

当有多个候选模型时，我们需要一些指标来选择最合适的模型：

AIC（赤池信息准则） 基于信息论，平衡了模型的拟合优度和复杂度：AIC = 2k - 2ln(L)

其中k是参数个数，L是似然函数值。AIC值越小，模型越好。

BIC（贝叶斯信息准则） 与AIC类似，但对模型复杂度的惩罚更大：BIC = kln(n) - 2ln(L)

同样，BIC值越小，模型越好。

三、综合评估流程与实践建议

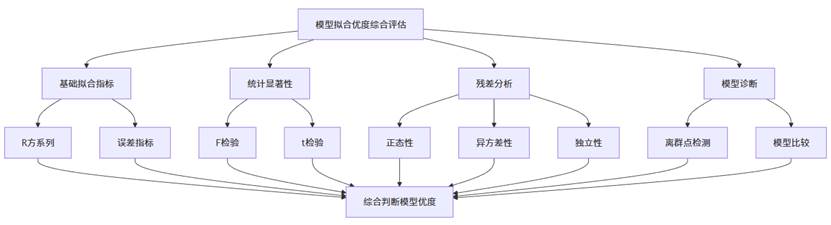
综合评估流程图整合了前文讨论的所有评估维度，展示了完整的模型评价体系。在实际研究中，我们需要综合考虑这些方面的结果，避免仅依赖单一指标做出判断，这样才能对模型质量有全面、准确的认识。

建立了一个回归模型后，如何进行系统性的评估？以下是建议的流程：

首先检查R²和调整R²：了解模型对数据的整体解释能力，但不要盲目追求高R²。
进行F检验和t检验：确认模型和各个自变量的统计显著性。
分析误差指标：了解模型的平均预测误差大小，结合业务背景判断是否可接受。
进行残差分析：检查回归假设是否满足，包括正态性、同方差性和独立性。
检测离群点和强影响点：识别可能对模型产生不当影响的观测点。
比较多个模型：如果有多个候选模型，使用AIC/BIC等指标进行比较。
最终业务解释：统计上最优的模型不一定在业务上最有用，需要结合专业知识和实际应用场景做最终判断。

结语：回归模型拟合优度评估是一个多维度、系统性的过程，需要综合考虑拟合指标、统计检验、残差分析和模型诊断结果。单一指标如R²虽然常用，但不能全面反映模型质量。

在实际研究中，建议使用专业统计软件如SPSSAU进行全面模型评估，这些工具提供了从基础拟合优度到高级诊断的一站式分析，大大简化了评估流程。但无论如何，统计指标都应与业务知识和研究目的结合，才能构建既有统计意义又有实用价值的回归模型。

记住，一个好的模型不仅要在统计上显著，更要在实际应用中有用。