空间滞后误差模型（SAC）详解，从理论到SPSSAU分析全流程

原创于 2025-12-16 10:24:35 发布 · 341 阅读

CC 4.0 BY-SA版权

文章标签：

在空间计量经济学的模型谱系中，空间杜宾模型（SDM）、空间滞后模型（SLM）和空间误差模型（SEM）已为研究者所熟知。然而，当数据生成过程同时受到因变量内生性交互效应与误差项空间自相关的共同影响时，一个更为一般化的模型便应运而生——空间滞后误差模型。该模型也被称为一般空间模型 或 SAC模型，它通过同时引入两种空间依赖结构，为我们提供了一个更为综合和稳健的分析框架，用以处理复杂的空间数据生成过程。

一、 SAC模型的理论内核：双重空间依赖的整合

SAC模型的核心思想在于，它同时承认并建模了两种不同类型的空间依赖性：

内生的空间交互效应：源于因变量之间的相互影响，即一个地区的因变量值直接受到邻近地区因变量值的影响。这体现了某种实质性的空间互动或扩散过程。
误差项的空间自相关：源于模型设定之外遗漏变量所具有的空间相关性，或者是由未观测到的共同冲击所导致。这种依赖性存在于扰动项中。

这种双重设定使得SAC模型具有极强的包容性。其数学模型表述如下：

y = ρWy + Xβ + u, u = λWu + ε

让我们解析这个模型的核心构成：

y = ρWy + Xβ + u：这部分与空间滞后模型（SLM）一致。
- y是因变量向量。
- Wy是因变量的空间滞后项，由空间权重矩阵 W 计算得出。
- ρ 是空间自回归系数，衡量了因变量空间依赖的强度，是模型的核心参数之一。
- X是自变量矩阵，β是其对应的回归系数。
- u是随机误差项。
u = λWu + ε：这部分与空间误差模型（SEM）一致。
- Wu是误差项 u 的空间滞后项。
- λ 是空间误差自相关系数，衡量了误差项空间依赖的强度，是另一个核心参数。
- ε 是服从独立同分布的随机扰动项。

SAC模型的理论定位非常明确： 当研究者有先验理论认为因变量存在空间溢出（如技术创新扩散、犯罪率模仿），同时又担心模型可能遗漏了具有空间相关性的重要变量时，SAC模型便成为一个理想的选择。它在理论上综合了SLM和SEM，能够同时控制这两种机制，避免因误设而导致的有偏估计。

其在空间模型家族中的位置，可以通过下图清晰地展现：

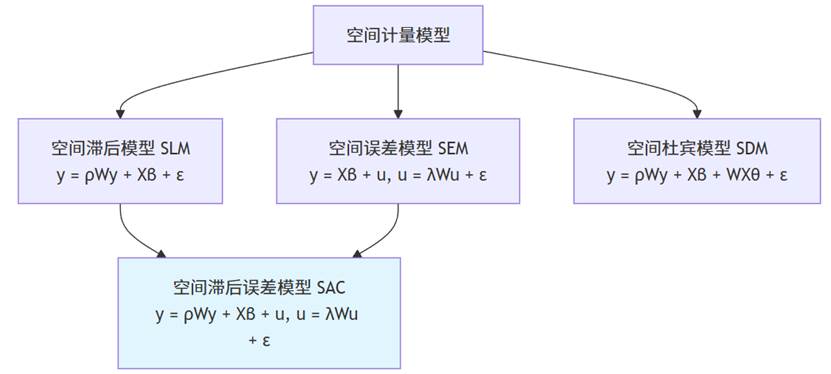
SAC模型在基础空间模型谱系中的定位。SAC模型可以视为SLM模型与SEM模型的直接结合，同时包含了因变量的空间滞后项和误差项的空间滞后项，形成了一个更为一般化的框架。

二、 SAC模型的分析框架与SPSSAU输出解读

在SPSSAU中执行SAC模型分析，会得到一套系统化的输出结果。理解每一部分输出的理论含义，是正确解读模型的关键。

1. 模型基本参数表：研究的“技术档案”

这张表格是分析报告的起点，它清晰地标定了研究的技术设定。

它明确了本研究所用的模型类型为“空间滞后误差模型（SAC）”、所使用的空间权重矩阵、其标准化方式（如行标准化）、样本量以及估计方法（如GMM估计法）。这些信息是评估模型设定正确性和结果可重复性的基础。SPSSAU在此清晰地列明这些参数，体现了分析的规范性与透明度。

2. 模型分析结果表：核心参数的估计

这是模型输出的核心，呈现了所有关键参数的估计值、标准误和显著性。

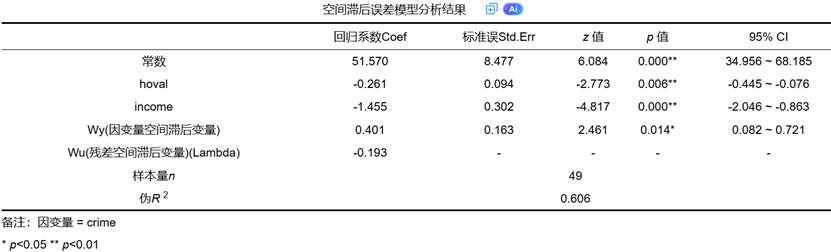
自变量回归系数（β）：反映了在同时控制了因变量空间依赖和误差项空间依赖之后，自变量对因变量的“净影响”。此时的估计更为纯净，是研究者关注的主要解释依据。
Wy的系数（ρ）：这是模型的关键参数之一。一个显著的 ρ 证实了因变量之间存在实质性的空间交互效应，即存在空间溢出或模仿行为。
Wu的系数（λ）：这是模型的另一个关键参数。一个显著的 λ 证实了误差项中存在空间自相关，意味着模型可能遗漏了重要的空间相关变量，或者存在空间性的共同冲击。
重要提示：在SAC模型中，ρ 和 λ 的估计是同时进行的。有时可能会出现其中一个不显著的情况，这本身也是一个有价值的发现，说明某种空间依赖性可能占主导地位。

3. 空间效应分解表

与SDM模型类似，由于存在因变量的空间滞后项（Wy），自变量的影响同样需要通过空间效应分解来准确解读，而不能直接看回归系数。

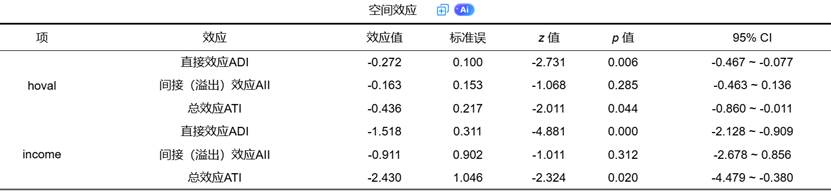
SPSSAU会将每个自变量的总影响分解为：

直接效应：衡量某一区域的自变量发生变化时，对该区域自身因变量的平均影响（包含了空间反馈效应）。
间接效应（溢出效应）：衡量某一区域的自变量发生变化时，通过空间传导机制对所有其他区域因变量的平均影响。
总效应：直接效应与间接效应之和。

这张表格是SAC模型最终结论的权威依据。 研究者需要基于此来判断一个自变量的影响是局部的还是全局的，其空间溢出的方向和强度如何。

4. 模型诊断与比较

残差正态性检验（如JB检验）：作为模型设定稳健性的辅助参考，但其重要性在极大似然估计中相对较低。

三、何时选择SAC模型？

选择SAC模型，通常基于以下考量：

理论驱动：研究问题本身暗示了强烈的空间互动（如政策模仿、技术扩散），同时又无法完全排除遗漏空间相关变量的风险。
统计检验：在模型筛选阶段，拉格朗日乘数（LM）检验结果同时拒绝了“无空间滞后”和“无空间误差”的原假设，提示两种空间依赖性可能并存。
稳健性考量：作为一个比SLM和SEM更一般的模型，将其作为稳健性检验的一部分，可以评估核心发现的稳定性。

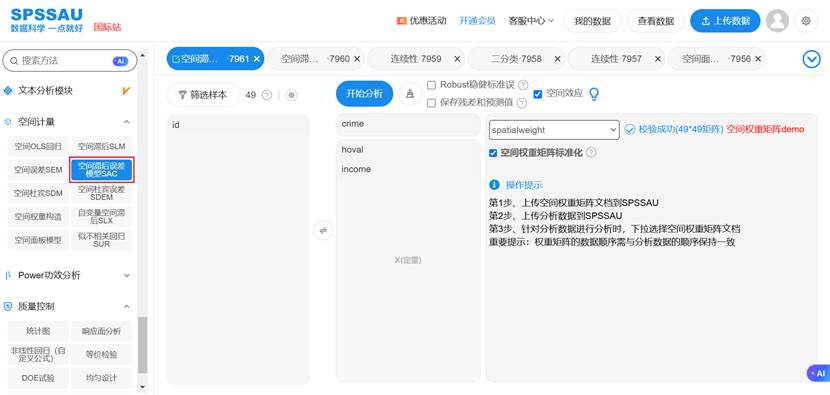
在这些场景下，SPSSAU展现了其强大的易用性与专业性：

一站式分析：用户只需选择“空间滞后误差模型（SAC）”，上传数据和空间权重矩阵，SPSSAU即可自动完成所有复杂的估计（如GMM法）和空间效应分解计算。
清晰的逻辑输出：SPSSAU的输出结构完全遵循前述分析流程，从基本参数到核心系数，再到最终的空间效应分解，引导用户进行逻辑清晰的解读。
智能化辅助：其内置的智能分析能自动提示关键参数（如 ρ 和 β）的显著性，帮助用户快速抓住模型的核心发现，降低了复杂模型的理解门槛。

四、总结

空间滞后误差模型（SAC）是空间计量经济学中一个功能强大而全面的模型。它通过同时建模因变量的空间依赖性和误差项的空间相关性，为研究者提供了一个处理复杂空间交互过程的综合工具箱。尽管其解释比基础模型稍显复杂，但在其适用的理论场景下，它能提供更为稳健和可靠的估计结果。

SPSSAU将这一高级计量模型完整而友好地呈现给所有研究者。通过其系统化的输出框架，用户可以轻松地完成从模型设定、参数估计到空间效应分解的全过程，从而能够将更多的精力投入到理论机制的阐释与政策含义的挖掘中。在追求研究严谨性与深度的今天，掌握并善用SAC模型及其分析工具，无疑将显著提升科研工作的质量与价值。