高等数学学习笔记 ☞ 映射

原创已于 2025-01-03 15:11:49 修改 · 1k 阅读

·

15

·

CC 4.0 BY-SA版权

版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。

文章标签：

#映射 #三要素

于 2024-12-24 14:37:08 首次发布

高等数学专栏收录该内容

20 篇文章

订阅专栏

1. 映射的定义

设X，Y为非空的集合，若存在法则 f，使得对于X中任意的元素 $x$ ，按照法则 f，在Y中都有唯一的元素 $y$ 与之对应，

则称法则 f为从X到Y的映射。记作：f：X $\rightarrow$ Y，其中：X称为原像，Y称为像。

备注：

①：函数仅仅属于映射的一种。

②：映射 f定义明确：允许一对一，多对一，但不允许一对多。

2. 映射的三要素

（1）定义域：记作 $D_{f}$ ，即映射 f的定义域就是 $D_{f}$ ，其中 $D_{f} = X$ 。

（2）值域：记作 $R_{f}$ ，即映射 f的值域就是 $R_{f}$ ，其中 $R_{f} = \left \{ f(x)|x\in X \right \}$ 。

（3）法则：记作 f，即所定义的规则。

备注：

①：对于集合X中的任意 $x$ ，它的像是唯一的；对于集合Y中的任意 $y$ ，它的原像不一定是唯一的。

②：映射 f的值域是 $R_{f}$ ，不是Y，其中： $R_{f}\subset Y$ 。

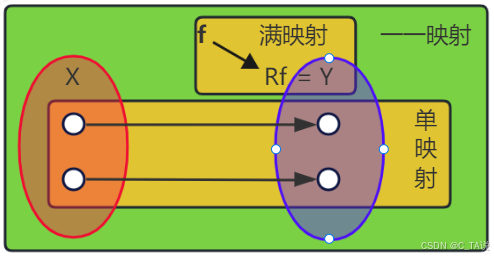
3. 映射的种类

（1）满射：映射 f的值域 $R_{f}$ 恰好为Y。

（2）单射：在定义域 $D_{f}$ 中任取元素 $x_{1}$ ， $x_{2}$ ( $x_{1}$ ≠ $x_{2}$ )，在值域 $R_{f}$ 中都有 $f(x_{1}) \neq f(x_{2})$ 。

（3）一一映射：同时满足满射和单射的映射。

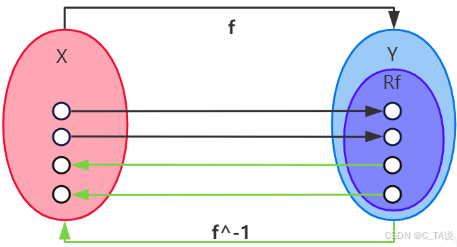
（4）逆映射：已知映射 $f:X\rightarrow Y$ 为单射，若对于值域 $R_{f}$ 中的任意元素 $y$ ，在定义域 $D_{f}$ 中都有唯一的元素 $x$ 与之对应，

则称法则 $f^{-1}$ 为从 $R_{f}$ 到 $X$ 的逆映射。记作： $f^{-1}:R_{f}\rightarrow X$ 。

备注：

（1）（2）（3）
（4）

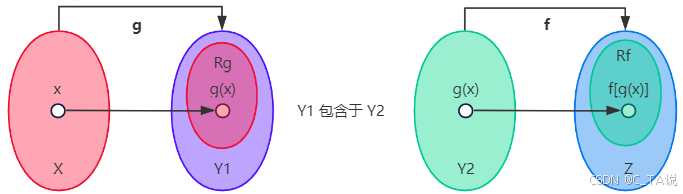
（5）复合映射：已知映射 $g:X\rightarrow Y_{1}$ ，映射 $f:Y_{2}\rightarrow Z$ ，其中 $Y_{1}\subset Y_{2}$ ，则称映射 $fog:X\rightarrow Z$ 为复合映射。

备注：映射 $g$ 的值域 $R_{g}$ 包含于映射 $f$ 的定义域内，即 $R_{g}\subset D_{f}$ 。

（5）

评论

成就一亿技术人!

拼手气红包6.0元

还能输入1000个字符 | 博主筛选后可见

添加红包

插入表情

表情包

代码片

HTML/XML
objective-c
Ruby
PHP
C
C++
JavaScript
Python
Java
CSS
SQL
其它

条评论被折叠查看

被折叠的条评论为什么被折叠?

到【灌水乐园】发言

查看更多评论

添加红包

成就一亿技术人!

hope_wisdom

发出的红包

实付元

使用余额支付

点击重新获取

扫码支付

钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。