【数学】期望、方差、协方差、协方差矩阵

期望、方差、协方差、协方差矩阵

1 期望（数学期望、均值）

---

• 在概率论和统计学中，数学期望(mean)（或均值，亦简称期望）是试验中每次可能结果的概率乘以其结果的总和，是最基本的数学特征之一。它反映随机变量平均取值的大小。
• 需要注意的是，期望值并不一定等同于常识中的“期望”——“期望值”也许与每一个结果都不相等。期望值是该变量输出值的平均数。期望值并不一定包含于变量的输出值集合里。
• 大数定律规定，随着重复次数接近无穷大，数值的算术平均值几乎肯定地收敛于期望值。

1.1 期望的定义

对于离散型随机变量和连续型随机变量期望的定义公式略有不同

离散型变量

连续型变量

2 方差

---

• 方差是在概率论和统计方差衡量随机变量或一组数据时离散程度的度量。
• 概率论中方差用来度量随机变量和其数学期望（即均值）之间的偏离程度。
• 统计中的方差（样本方差）是每个样本值与全体样本值的平均数之差的平方值的平均数。
• 在许多实际问题中，研究方差即偏离程度有着重要意义。

即，方差是衡量源数据和期望值相差的度量值。

2.1 方差的定义

方差在统计描述和概率分布中各有不同的定义，并有不同的公式。

统计描述的定义

• 在统计描述中，方差用来计算每一个变量（观察值）与总体均数之间的差异。
• 为避免出现离均差总和为零，离均差平方和受样本含量的影响，统计学采用平均离均差平方和来描述变量的变异程度。总体方差计算公式：

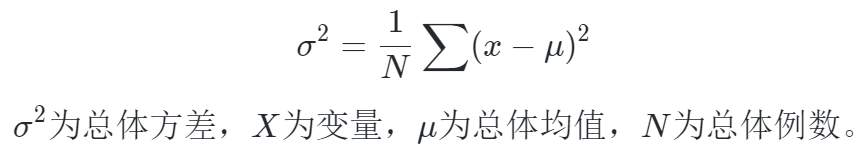
• 实际工作中，总体均数难以得到时，应用样本统计量代替总体参数，经校正后，样本方差计算公式：

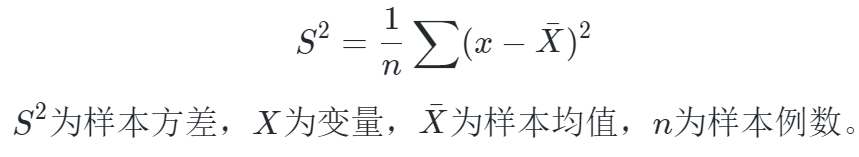
概率分布中的定义

• 在概率分布中，设X是一个离散型随机变量，若下式存在，则称下式为X的方差，记为D(X)或Var(X)

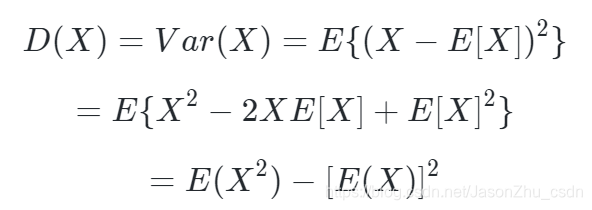
此时定义下式为标准差，或均方差。

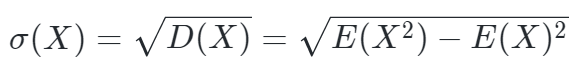
• 方差用来度量变量X与其均值E(X)的偏离程度(即衡量X取值分散程度的一个尺度)

方差实际上是随机变量函数g(X)的数学期望

离散随机变量

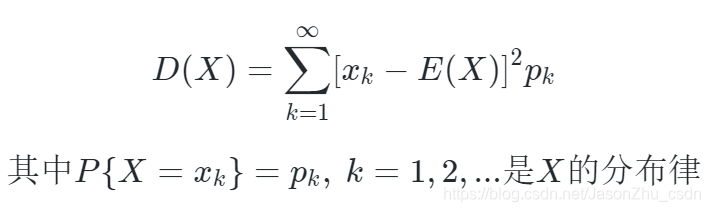
连续随机变量

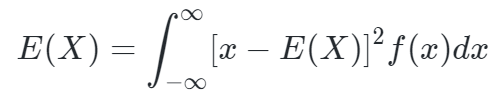
3 协方差

---

• 协方差（Covariance）在概率论和统计学中用于衡量两个变量的总体误差。
• 而方差是协方差的一种特殊情况，即当两个变量是相同的情况。

1.3.1 协方差的定义

如果随机变量X和Y是相互独立的，则

因此当上式不等于0时，意味着X、Y存在一定的关系

定义： 期望值分别为E(X)与E(Y)的两个实随机变量X与Y之间的协方差Cov(X,Y)定义为：

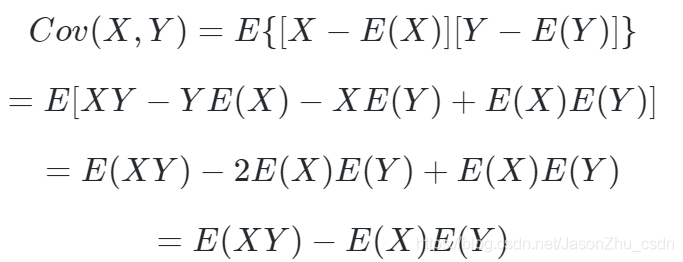
同时,定义随机变量X与Y的相关系数为

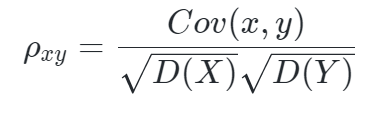
协方差的性质

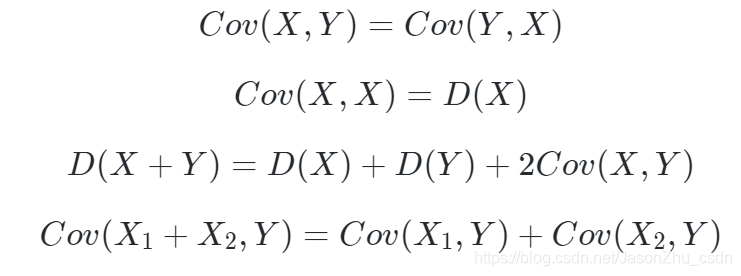
协方差特点

• 从直观上来看，协方差表示的是两个变量总体误差的期望，这与只表示一个变量误差的方差不同。
• 如果两个变量的变化趋势一致，也就是说如果其中一个大于自身的期望值时另外一个也大于自身的期望值，那么两个变量之间的协方差就是正值；
• 如果两个变量的变化趋势相反，即其中一个变量大于自身的期望值时另外一个却小于自身的期望值，那么两个变量之间的协方差就是负值。
• 如果X与Y是统计独立的，那么二者之间的协方差就是0，因为两个独立的随机变量满足E(XY)=E(X)E(Y)。
• 但是，反过来并不成立。即如果X与Y的协方差为0，二者并不一定是统计独立的。
• 协方差Cov(X,Y)的度量单位是X的协方差乘以Y的协方差。而取决于协方差的相关性，是一个衡量线性独立的无量纲的数。
• 协方差为0的两个随机变量称为是不相关的。

参考链接

4 协方差矩阵

---

4.1 矩

• 设存在随机变量X,Y 若下式存在，称它为X的k阶原点矩，简称k阶矩。

• 设存在随机变量X,Y 若下式存在，称它为X的k阶中心矩。

• 设存在随机变量X,Y 若下式存在，称它为X的k+l阶混合矩。

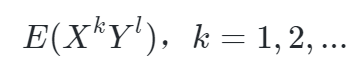
• 设存在随机变量X,Y 若下式存在，称它为X的k+l阶混合中心矩。

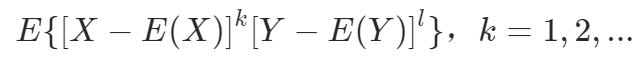
• 示例：

1. E(X)是一阶原点矩
2. D(X)是二阶中心距
3. Cov(X,Y)是二阶混合中心距

4.2 协方差矩阵

将n维变量的二阶混合中心距排列成矩阵，即得n维变量的协方差矩阵