求最近公共祖先LCA（四种方法：倍增、Tarjan、树剖、ST表）

阐上

已于 2022-09-05 11:13:38 修改

阅读量3.5k

点赞数 4

CC 4.0 BY-SA版权

分类专栏：知识点笔记文章标签：算法 LCA 树动态规划 c++

于 2021-12-13 14:47:12 首次发布

本文链接：https://blog.youkuaiyun.com/weixin_51797626/article/details/121904720

知识点笔记专栏收录该内容

23 篇文章

订阅专栏

本文探讨了四种高效算法：倍增法用于在线处理最大次大边权，Tarjan并查集优化用于离线查询距离和祖先，树链剖分简化LCA查询，以及ST表实现O(1)查询LCA。通过实例展示了如何在各种场景下利用这些方法解决实际问题。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

1. 倍增法（最常用的在线处理方法）：

用一个数组 $f [i] [j]$ 记录从 i 点出发向上跳 $2^j$ 步能抵达的点的编号

朴素版的方法就是往上一路搜到祖先（每次跳一步），但倍增可以跳 2 的指数倍的步数，这样就大大缩减了跳跃的时间，降低算法的时间复杂度

预处理 $O (n l o g n)$ ，查询 $O (l o g n)$

————————————————————————————————————————

记录祖先 or 记录路径长度

代码：

int h[N], e[M], ne[M], w[M], idx;
int dist[N], dep[N];
int fa[N][14];

void add(int a, int b, int x) {
	e[idx] = b, w[idx] = x, ne[idx] = h[a], h[a] = idx++;
}

void bfs(int x) {
	mem(dep, -1);
	queue<int> q;
	q.push(x);
	dep[0] = 0, dep[x] = 1;
	while (q.size())
	{
		int t = q.front();
		q.pop();
		for (int i = h[t]; ~i; i = ne[i]) {
			int j = e[i];
			if (dep[j] == -1) {
				q.push(j);
				dep[j] = dep[t] + 1;
				dist[j] = dist[t] + w[i];
				fa[j][0] = t;
				for (int k = 1; k <= 13; k++)//bug —— 加分号...
					fa[j][k] = fa[fa[j][k - 1]][k - 1];

			}
		}
	}
}

int lca(int a, int b) {
	if (dep[a] < dep[b])swap(a, b);
	for (int i = 13; i >= 0; i--)
		if (dep[fa[a][i]] >= dep[b])
			a = fa[a][i];
	if (a == b)return a;
	for (int i = 13; i >= 0; i--)
		if (fa[a][i] != fa[b][i]) {
			a = fa[a][i];
			b = fa[b][i];
		}
	return fa[a][0];
}

—————————————————————————————————————————————

维护路径 Max or Min 边权

int h[N], e[M], ne[M], w[M], idx;
int p[N], dep[N], q[N];
int fa[N][17], d1[N][17], d2[N][17];

void add(int a, int b, int x) {
	e[idx] = b, w[idx] = x, ne[idx] = h[a], h[a] = idx++;
}

void bfs(int x) {
	mem(dep, -1);
	dep[0] = 0, dep[x] = 1;
	queue<int> q;
	q.push(x);

	while (q.size())
	{
		int t = q.front();
		q.pop();
		for (int i = h[t]; ~i; i = ne[i]) {
			int j = e[i];
			if (dep[j] == -1) {
				dep[j] = dep[t] + 1;
				q.push(j);

				fa[j][0] = t;
				d1[j][0] = w[i], d2[j][0] = -INF;
				for (int k = 1; k <= 16; k++) {
					int anc = fa[j][k - 1];
					fa[j][k] = fa[anc][k - 1];

					int dist[] = { d1[j][k - 1],d2[j][k - 1],d1[anc][k - 1],d2[anc][k - 1] };
					d1[j][k] = d2[j][k] = -INF;
					for (int u = 0; u < 4; u++) {
						int d = dist[u];
						if (d > d1[j][k])d2[j][k] = d1[j][k], d1[j][k] = d;
						else if (d != d1[j][k] && d > d2[j][k])d2[j][k] = d;
						//视情况修改，维护 严格 or 非严格 最大次大
					}
				}
			}
		}
	}
}

int lca(int a, int b, int x) {
	//开数组存储路径上所有最大次大
	int distan[N * 2];
	int cnt = 0;
	if (dep[a] < dep[b])swap(a, b);
	for (int j = 16; j >= 0; j--)
		if (dep[fa[a][j]] >= dep[b]) {
			distan[cnt++] = d1[a][j];
			distan[cnt++] = d2[a][j];
			a = fa[a][j];
		}
	if (a != b) {
		for (int j = 16; j >= 0; j--)
			if (fa[a][j] != fa[b][j]) {
				distan[cnt++] = d1[a][j];
				distan[cnt++] = d2[a][j];
				distan[cnt++] = d1[b][j];
				distan[cnt++] = d2[b][j];
				a = fa[a][j], b = fa[b][j];
			}
		distan[cnt++] = d1[a][0];
		distan[cnt++] = d1[b][0];
	}

	int dist1 = -INF, dist2 = -INF;
	for (int i = 0; i < cnt; i++) {
		int d = distan[i];
		if (d > dist1)dist2 = dist1, dist1 = d;
		else if (d != dist1 && d > dist2)dist2 = d;
	}

	if (x > dist1)return x - dist1;
	if (x > dist2)return x - dist2;
	return INF;
}

Acwing：严格次小生成树（求两点间路径上最大边的权值）(模板)

洛谷：严格次小生成树

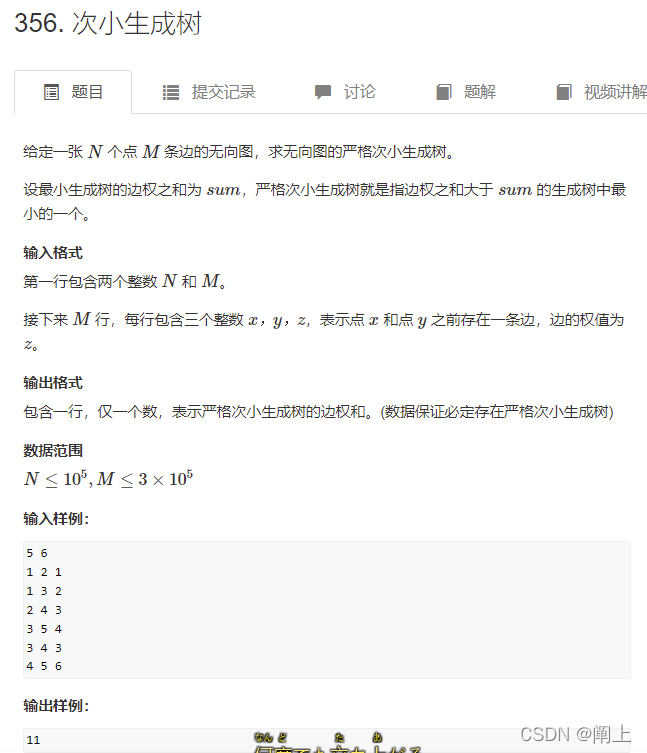
在这里插入图片描述
求两点间路径上最大边的权值，就不能通过前缀和了，会丢失信息。每个结点存到其他结点的路径最大边权又占用过多空间 $O(n^2)$

因此学习下倍增优化存点的思想，将这空间二进制压缩成 $O(nlog_2n)$

维护一个 $d [i] [j]$ ，维护从 i 点往上跳 $2^j$ 步这条路径上的最大边权

如果是求 $严格次小树$ 那就要维护一个最大 d1 和一个次大 d2 数组。最后 lca 求最近公共祖先时，随时记录每一条路径（二进制压缩过，但累计在一起信息不会丢失），就能得出两点间路径的最大和次大边权了

———————————————————————————————————————————

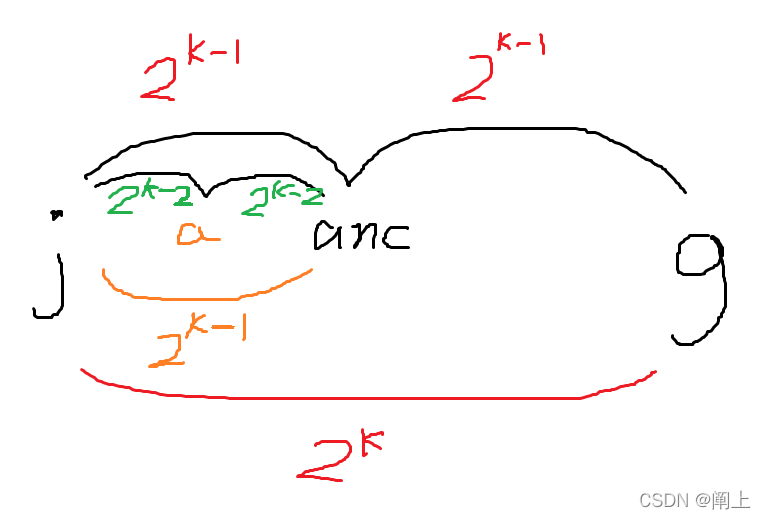
以下代码可以据图理解（倍增的核心!）：

for (int k = 1; k <= 16; k++) {
	int anc = fa[j][k - 1];
	fa[j][k] = fa[anc][k - 1];
}

在这里插入图片描述
代码：

#include<bits/stdc++.h>
#include<unordered_set>
#include<unordered_map>
#define mem(a,b) memset(a,b,sizeof a)
#define cinios (ios::sync_with_stdio(false),cin.tie(0),cout.tie(0))
#define sca scanf
#define pri printf
#define ul u << 1
#define ur u << 1 | 1
//#pragma GCC optimize(2)
//[博客地址](https://blog.youkuaiyun.com/weixin_51797626?t=1) 
using namespace std;

typedef long long ll;
typedef pair<int, int> PII;

const int N = 100010, M = N << 1, MM = 3000010;
int INF = 0x3f3f3f3f, mod = 100003;
ll LNF = 0x3f3f3f3f3f3f3f3f;
int n, m, k, T, S, D;
int h[N], e[M], ne[M], w[M], idx;
int p[N], dep[N], q[N];
int fa[N][17], d1[N][17], d2[N][17];

struct edge
{
	int l, r, w;
	bool tree;
	bool operator <(const edge& t)const {
		return w < t.w;
	}
}ed[N * 3];

void add(int a, int b, int x) {
	e[idx] = b, w[idx] = x, ne[idx] = h[a], h[a] = idx++;//bug —— h[a]++
}

int find(int x) {
	if (p[x] != x)p[x] = find(p[x]);
	return p[x];
}

ll kruskal() {
	mem(h, -1);
	sort(ed, ed + m);
	for (int i = 1; i <= n; i++)p[i] = i;

	ll res = 0;
	for (int i = 0; i < m; i++) {
		int a = ed[i].l, b = ed[i].r, w = ed[i].w;
		int fa = find(a), fb = find(b);
		if (fa != fb) {
			res += w;
			ed[i].tree = true;
			add(a, b, w), add(b, a, w);//随时建这颗最小生成树
			p[fa] = fb;
		}
	}
	return res;
}

void bfs() {
	mem(dep, 0x3f);
	dep[0] = 0, dep[1] = 1;
	int hh = 0, tt = 0;
	q[tt++] = 1;

	while (hh < tt)
	{
		int t = q[hh++];
		for (int i = h[t]; ~i; i = ne[i]) {
			int j = e[i];
			if (dep[j] > dep[t] + 1) {
				dep[j] = dep[t] + 1;
				q[tt++] = j;

				fa[j][0] = t;
				d1[j][0] = w[i], d2[j][0] = -INF;
				for (int k = 1; k <= 16; k++) {
					int anc = fa[j][k - 1];
					fa[j][k] = fa[anc][k - 1];

					//j 跳 2^k 步可以拆分成两部分：
					//先跳 2^k-1 步到anc点，再跳 2^k-1 步到终点
					//两段跳跃都有一个区间最大次大值，都记录下来
					int dist[] = { d1[j][k - 1],d2[j][k - 1],d1[anc][k - 1],d2[anc][k - 1] };
					d1[j][k] = d2[j][k] = -INF;//不能忘记此 k 处最大次大的初始化

					for (int u = 0; u < 4; u++) { //枚举每一种再维护新最大次大即可
						int d = dist[u];
						if (d > d1[j][k])d2[j][k] = d1[j][k], d1[j][k] = d;
						else if (d != d1[j][k] && d > d2[j][k])d2[j][k] = d;
					}
				}
			}
		}
	}
}

int lca(int a, int b, int x) {
	int distan[N * 2];//此处如果用vector的话测12组数据会多出400多ms的常数时间
	//容器还是要少用啊
	int cnt = 0;
	if (dep[a] < dep[b])swap(a, b);
	for (int j = 16; j >= 0; j--)
		if (dep[fa[a][j]] >= dep[b]) {
			distan[cnt++] = d1[a][j];//向上跳一段距离，这段距离的最大次大都记录下来
			distan[cnt++] = d2[a][j];
			a = fa[a][j];
		}
	if (a != b) {
		for (int j = 16; j >= 0; j--)
			if (fa[a][j] != fa[b][j]) {
				distan[cnt++] = d1[a][j];
				distan[cnt++] = d2[a][j];
				distan[cnt++] = d1[b][j];
				distan[cnt++] = d2[b][j];
				a = fa[a][j], b = fa[b][j];
			}
		distan[cnt++] = d1[a][0];
		distan[cnt++] = d1[b][0];
		//distan[cnt++](d2[a][0]);
		//不需要添加这段次大，因为只向上跳一步，显然只有最大没有次大
	}
	
	//对这样全部记录的数据，显然不会漏情况，肯定能得到 a 点到 b 点的最大次大
	int dist1 = -INF, dist2 = -INF;
	for (int i = 0; i < cnt; i++) {
		int d = distan[i];
		if (d > dist1)dist2 = dist1, dist1 = d;
		else if (d != dist1 && d > dist2)dist2 = d;
	}

	//bug —— dist1 < x ，显然若求次小生成树，添加的非树边 x 要大于树中找到的最大次大边
	if (x > dist1)return x - dist1;
	if (x > dist2)return x - dist2;
	return INF;
}

int main() {
	cinios;

	cin >> n >> m;
	for (int i = 0; i < m; i++) {
		int a, b, x;
		cin >> a >> b >> x;
		ed[i] = { a,b,x };
	}
	
	ll sum = kruskal();
	bfs();

	ll ans = LNF;
	for (int i = 0; i < m; i++) {
		if (!ed[i].tree) {
			int a = ed[i].l, b = ed[i].r, w = ed[i].w;
			ans = min(ans, sum + lca(a, b, w));//lca返回的是删去边加新边之后的增加值
		}
	}
	cout << ans;

	return 0;
}

——————————————————————————————————————————————

洛谷：货车运输（求两点间路径上最小边的权值）

在这里插入图片描述
理解了求严格次小生成树那道题的做法，此题就很简单了，不过需要动脑筋贪心思维一下

#include<bits/stdc++.h>
#include<unordered_set>
#include<unordered_map>
#define mem(a,b) memset(a,b,sizeof a)
#define cinios (ios::sync_with_stdio(false),cin.tie(0),cout.tie(0))
#define sca scanf
#define pri printf
#define ul u << 1
#define ur u << 1 | 1
//#pragma GCC optimize(2)
//[博客地址](https://blog.youkuaiyun.com/weixin_51797626?t=1) 
using namespace std;

typedef long long ll;
typedef pair<int, int> PII;

const int N = 10010, M = N << 1, MM = 3000010;
int INF = 0x3f3f3f3f, mod = 100003;
ll LNF = 0x3f3f3f3f3f3f3f3f;
int n, m, k, T, S, D;
int h[N], e[M], ne[M], w[M], idx;
int p[N], q[N];
int dep[N];
int fa[N][14], d1[N][14];
bool st[N];

struct edge
{
	int l, r, w;
	bool operator <(const edge& t)const {
		return w > t.w;
	}
}ed[N * 5];

void add(int a, int b, int x) {
	e[idx] = b, w[idx] = x, ne[idx] = h[a], h[a] = idx++;//bug —— h[a]++
}

int find(int x) {
	if (p[x] != x)p[x] = find(p[x]);
	return p[x];
}

void kruskal() {
	mem(h, -1);
	sort(ed, ed + m);
	for (int i = 1; i <= n; i++)p[i] = i;

	for (int i = 0; i < m; i++) {
		int a = ed[i].l, b = ed[i].r, w = ed[i].w;

		int fa = find(a), fb = find(b);
		if (fa != fb) {
			add(a, b, w), add(b, a, w);//随时建这颗最小生成树
			p[fa] = fb;
		}
	}
}

void bfs(int x) {
	dep[x] = 1;
	int hh = 0, tt = 0;
	q[tt++] = x;

	while (hh < tt)
	{
		int t = q[hh++];
		for (int i = h[t]; ~i; i = ne[i]) {
			int j = e[i];
			if (dep[j] > dep[t] + 1) {
				dep[j] = dep[t] + 1;
				q[tt++] = j;

				fa[j][0] = t;
				d1[j][0] = w[i];
				for (int k = 1; k <= 13; k++) {
					int anc = fa[j][k - 1];
					fa[j][k] = fa[anc][k - 1];
					d1[j][k] = min(d1[j][k - 1], d1[anc][k - 1]);
					//d1[anc][k - 1]不能保证一定有值，跳过头anc就是0
					//如果未初始化INF极值，d1[0][k]的值为0，影响取min
				}
			}
		}
	}
}

int lca(int a, int b) {
	int mi = INF;
	if (dep[a] < dep[b])swap(a, b);
	for (int j = 13; j >= 0; j--)//bug —— j = 14，数组越界了
		if (dep[fa[a][j]] >= dep[b]) {
			mi = min(mi, d1[a][j]);
			a = fa[a][j];
		}
	if (a != b) {
		for (int j = 13; j >= 0; j--)
			if (fa[a][j] != fa[b][j]) {
				mi = min({ mi, d1[a][j], d1[b][j] });
				a = fa[a][j];
				b = fa[b][j];
			}
		mi = min({ mi,d1[a][0],d1[b][0] });
	}
	return mi;
}

int main() {
	cinios;

	cin >> n >> m;
	for (int i = 0; i < m; i++) {
		int a, b, x;
		cin >> a >> b >> x;
		ed[i] = { a,b,x };
	}

	kruskal();

	mem(dep, 0x3f);
	mem(d1, 0x3f);//bug —— 未初始化 d1 数组极大值（维护min）
	dep[0] = 0;
	for (int i = 1; i <= n; i++) {
		int fi = find(i);
		if (!st[fi]) {
			st[fi] = true;
			bfs(fi);
		}
	}

	cin >> k;
	while (k--)
	{
		int a, b;
		cin >> a >> b;
		if (find(a) != find(b))cout << -1;
		else cout << lca(a, b);
		cout << '\n';
	}

	return 0;
}
/*
7 5
1 2 3
1 3 9
3 4 6
5 6 7
6 7 8
100
*/

——————————————————————————————————————————

2. Tarjan算法（并查集优化朴素查找）（离线处理）：

只能求距离和祖先

本质上是在 dfs 时将树中的点分成三种：
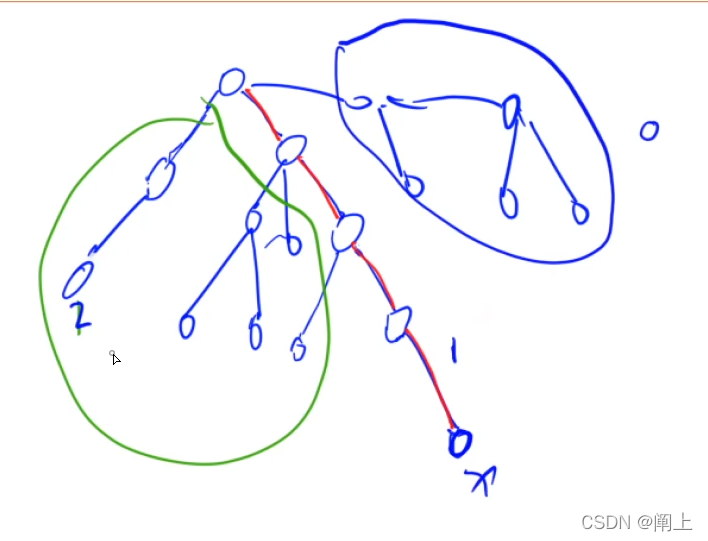
在这里插入图片描述
$0$ ：未处理到的点
$1$ ：正在处理的点（会形成一条链，该链也称为 1 链）
$2$ ：处理完毕的点

通过并查集将处理完毕的 2 类点连到 1 链上，1 链上的某点必定是某个子树上的点的父节点。

因此，查询 1 类点的询问时，如果询问的对象是 2 类点，两点的最近公共祖先必定是 2 类点的并查集父节点

因为是离线算法，整体能做到 $O (n + m)$ (遍历图)

——————————————————————————————————————————

Acwing：距离（同一题不同解法）

#include<bits/stdc++.h>
#include<unordered_set>
#include<unordered_map>
#define mem(a,b) memset(a,b,sizeof a)
#define cinios (ios::sync_with_stdio(false),cin.tie(0),cout.tie(0))
#define sca scanf
#define pri printf
#define ul u << 1
#define ur u << 1 | 1
//#pragma GCC optimize(2)
//[博客地址](https://blog.youkuaiyun.com/weixin_51797626?t=1) 
using namespace std;

typedef long long ll;
typedef pair<int, int> PII;

const int N = 10010, M = N << 1, MM = 3000010;
int INF = 0x3f3f3f3f, mod = 100003;
ll LNF = 0x3f3f3f3f3f3f3f3f;
int n, m, k, T, S, D;
int h[N], e[M], ne[M], w[M], idx;
int dist[N], p[N];
int st[N];
vector<PII> q[N];//记录询问，离线处理
int ans[M];//处理出每个询问的答案

void add(int a, int b, int x) {
	e[idx] = b, w[idx] = x, ne[idx] = h[a], h[a] = idx++;
}

int find(int x) {
	if (p[x] != x)p[x] = find(p[x]);
	return p[x];
}

void dfs(int x, int fa) {
	for (int i = h[x]; ~i; i = ne[i]) {
		int j = e[i];
		if (j == fa)continue;
		dist[j] = dist[x] + w[i];//同样维护一个前缀和到根的距离
		dfs(j, x);
	}
}

void tarjan(int x) {
	st[x] = 1;//当前遍历到的标记为 1
	for (int i = h[x]; ~i; i = ne[i]) {
		int j = e[i];
		if (!st[j]) { //处理子树
			tarjan(j);
			p[j] = x;//处理完后就将它连到 1 链上
		}
	}

	for (auto t : q[x]) {
		int ver = t.first, id = t.second;
		if (st[ver] == 2) { //唯有被处理完后的点才能拿来获得答案
			int fa = find(ver);
			//查看该点的父节点在 1 链上的位置
			ans[id] = dist[ver] + dist[x] - 2 * dist[fa];
		}
	}
	st[x] = 2;//处理完毕的标记为 2
	//未处理到的为 0
}

int main() {
	cinios;

	cin >> n >> m;
	mem(h, -1);
	for (int i = 1; i <= n; i++)p[i] = i;

	for (int i = 1; i < n; i++) {
		int a, b, x;
		cin >> a >> b >> x;
		add(a, b, x), add(b, a, x);
	}

	for (int i = 0; i < m; i++)
	{
		int a, b;
		cin >> a >> b;
		if (a != b) { //相同显然ans[i]为 0
			q[a].push_back({ b,i });
			q[b].push_back({ a,i });//记录询问的点和回答的编号
		}
	}

	dfs(1, -1);
	tarjan(1);

	for (int i = 0; i < m; i++)
		cout << ans[i] << '\n';

	return 0;
}

3. 树链剖分求LCA（常数和空间都会小一点）

思路就是用树剖把树变成一维序列，爬山法查询两点 LCA；

预处理 $O (n + m)$ ，查询 $O (l o g n)$

实际查询通常不会到 log 上限，常数比较小。

int dep[N], siz[N], top[N], son[N], fa[N];
int rid[N], id[N], idd;

void dfs_son(int x, int f, int d) {
    fa[x] = f, dep[x] = d; siz[x] = 1;
    for (int i = h[x]; ~i; i = ne[i]) {
        int j = e[i]; if (j == f)continue;
        dfs_son(j, x, d + 1);
        siz[x] += siz[j];
        if (siz[son[x]] < siz[j])son[x] = j;
    }
}
void dfs_top(int x, int t) {
    top[x] = t; id[x] = ++idd; rid[idd] = x;
    if (!son[x])return;
    dfs_top(son[x], t);
    for (int i = h[x]; ~i; i = ne[i]) {
        int j = e[i]; 
        if (j == fa[x] || j == son[x])continue;
        dfs_top(j, j);
    }
}

int lca(int u, int v) {
    while (top[u] != top[v])
    {
        if (dep[top[u]] < dep[top[v]])swap(u, v);
        u = fa[top[u]];
    }
    //选最上端dep小的
    return dep[u] < dep[v] ? u : v;
}

4. 树上预处理 ST 表实现 O(1) 查询 LCA （离线处理）

ST表和 Tarjan 都是离线处理，但 Tarjan 需要记录询问，看花眼了容易出bug。ST表相对而言不易出错。

此算法基于树上欧拉遍历序，对一棵树遍历出一个欧拉序（dfs遍历这颗树经过每个节点的顺序），同时我们记录每个点的深度：

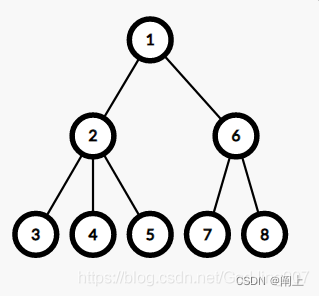
在这里插入图片描述
欧拉遍历序为：1 2 3 2 4 2 5 2 1 6 7 6 8 6 1
节点深度：0 1 2 1 2 1 2 1 0 1 2 1 2 1 0

现在记录下每个节点第一次出现的顺序，那么任意节点的 LCA 就是这两个点第一次出现的位置之间深度最小的点。

我们只需要对 dfs序 预处理 ST 表即可，最后就会变成 O(1) 的区间最小值查询问题。

预处理 $O (n l o g n)$ ，查询 $O (1)$

#include<bits/stdc++.h>
#include<unordered_map>
#define debug cout << "debug---  "
#define debug_ cout << "\n---debug---\n"
#define oper(a) operator<(const a& ee)const
#define forr(a,b,c) for(int a=b;a<=c;a++)
#define mem(a,b) memset(a,b,sizeof a)
#define cinios (ios::sync_with_stdio(false),cin.tie(0),cout.tie(0))
#define all(a) a.begin(),a.end()
#define sz(a) (int)a.size()
#define endl "\n"
#define ul (u << 1)
#define ur (u << 1 | 1)
using namespace std;

typedef unsigned long long ull;
typedef long long ll;
typedef pair<ll, int> PII;

const int N = 5e5 + 10, M = 2e6 + 10, mod = 1e9 + 7;
int INF = 0x3f3f3f3f; ll LNF = 0x3f3f3f3f3f3f3f3f;
int n, m, B = 10, ki;

int h[N], e[M], ne[M], idx;
void add(int a, int b) {
    e[idx] = b, ne[idx] = h[a], h[a] = idx++;
}
int dep[N], dfn[N << 1], tim, fir[N];

void dfs(int x, int f, int d) {
    dep[x] = d, dfn[++tim] = x;
    fir[x] = tim;
    //记录在dfs序中第一次出现的位置
    for (int i = h[x]; ~i; i = ne[i]) {
        int j = e[i];
        if (j == f)continue;
        dfs(j, x, d + 1);
        dfn[++tim] = x; 
        //回溯节点也要记录
    }
}

int f[N << 1][20];
int lg[N << 1];//预处理log2(N)

void RMQ(int nn) {
    for (int j = 0; (1 << j) <= nn; j++)
        for (int i = 1; i + (1 << j) - 1 <= nn; i++)
            if (!j) {
                f[i][j] = dfn[i];
                if (i > 1)lg[i] = lg[i >> 1] + 1;
            }
            else {
                int a = f[i][j - 1], b = f[i + (1 << j - 1)][j - 1];
                if (dep[a] <= dep[b])f[i][j] = a;
                else f[i][j] = b;
            }
}

int query(int l, int r) {
    l = fir[l], r = fir[r];
    if (l > r)swap(l, r);
    int k = lg[r - l + 1];
    int a = f[l][k], b = f[r - (1 << k) + 1][k];
    return dep[a] <= dep[b] ? a : b;
}

void solve() {
    int root;
    cin >> n >> m >> root;
    mem(h, -1);

    for (int i = 1; i < n; i++) {
        int a, b;
        cin >> a >> b;
        add(a, b), add(b, a);
    }

    dfs(root, 0, 0);

    RMQ(tim);

    while (m--)
    {
        int a, b;
        cin >> a >> b;
        cout << query(a, b) << '\n';
    }
}

signed main() {
    cinios;
    int T = 1;
    for (int t = 1; t <= T; t++) {
        solve();
    }
    return 0;
}
/*
*/
//板子