💥💥💞💞欢迎来到本博客❤️❤️💥💥
🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。
⛳️座右铭:行百里者,半于九十。
📋📋📋本文内容如下:🎁🎁🎁
⛳️赠与读者
👨💻做科研,涉及到一个深在的思想系统,需要科研者逻辑缜密,踏实认真,但是不能只是努力,很多时候借力比努力更重要,然后还要有仰望星空的创新点和启发点。建议读者按目录次序逐一浏览,免得骤然跌入幽暗的迷宫找不到来时的路,它不足为你揭示全部问题的答案,但若能解答你胸中升起的一朵朵疑云,也未尝不会酿成晚霞斑斓的别一番景致,万一它给你带来了一场精神世界的苦雨,那就借机洗刷一下原来存放在那儿的“躺平”上的尘埃吧。
或许,雨过云收,神驰的天地更清朗.......🔎🔎🔎
💥第一部分——内容介绍
基于模拟退火算法的太阳能-风能-水力混合抽水蓄能系统优化研究
摘要
针对太阳能、风能间歇性导致的电力供应不稳定问题,本文提出基于模拟退火算法(SA)的混合能源系统优化框架。通过构建包含经济性、可靠性和环境效益的多目标函数,结合变速抽水蓄能机组动态特性建模,实现风光出力波动平抑与储能资源高效配置。实验表明,SA算法较传统方法降低系统综合成本12.7%,弃电率下降36.8%,验证了其在复杂非线性约束条件下的全局优化能力。
关键词
模拟退火算法;混合抽水蓄能;多能互补;变速机组;弃电率优化
1. 引言
1.1 研究背景
全球能源转型背景下,可再生能源装机容量快速增长。截至2025年,中国风电、光伏累计装机突破12亿千瓦,但其间歇性导致电网调峰压力激增。抽水蓄能作为唯一规模化储能技术,全球装机容量达129GW,其中亚太地区占比66.4%。混合太阳能-风能-水力抽水蓄能系统(SWH-PHS)通过多能互补模式,可有效提升新能源消纳能力。
1.2 问题提出
传统定速抽水蓄能机组因功率调节刚性,难以适应风光出力强波动性。现有研究多聚焦单一能源优化,缺乏对变速机组动态特性与风光时空耦合的系统建模。元启发式算法在处理高维非线性约束时易陷入局部最优,需开发兼顾经济性与可靠性的鲁棒优化方法。
2. 系统建模与问题描述
2.1 混合系统工作原理
SWH-PHS系统包含光伏阵列、风力发电机组、变速抽水蓄能电站及电池储能单元。光伏和风机将可再生能源转化为电能,直接供给负载或充电蓄能系统。变速机组通过变频器实现转速-功率解耦控制,调节范围扩展至±30%额定功率,较定速机组提升调节灵活性47%。电池储能用于快速响应短时功率波动,弥补水力响应速度的不足。
2.2 数学模型构建
2.2.1 目标函数
采用加权和法构建多目标函数:

2.2.2 约束条件
3. 模拟退火算法优化框架
3.1 算法改进策略
- 自适应温度调度:采用指数降温计划 Tk+1=αTk,其中初始温度 T0=1000,降温速率 α=0.95
- 智能扰动策略:在当前解附近生成新解时,对抽水功率和电池充放电功率采用高斯扰动,标准差随温度降低动态调整
- 分布鲁棒优化:构建包含1-范数与∞-范数的模糊集合,刻画风光出力的不确定性,引入条件风险价值(CVaR)约束
3.2 优化流程设计
- 初始化阶段:生成随机调度方案,包含抽水时段、功率分配及电池SOC轨迹
- 迭代优化阶段:
- 计算当前解与新解的能量差 ΔE=f(xnew)−f(xcurrent)
- 若 ΔE<0 或满足Metropolis准则 e−ΔE/T>rand,则接受新解
- 终止条件:温度降至 Tmin=0.1 或达到最大迭代次数 Nmax=5000
4. 实验验证与结果分析
4.1 实验设置
选取中国西部某地区为研究对象,系统配置:
- 光伏:5MW(跟踪式支架)
- 风电机组:3×2MW(变桨距控制)
- 变速抽蓄:2×50MW(额定水头450m)
- 负荷:峰值8MW,日波动率1.8
4.2 算法性能对比
| 算法类型 | 综合成本(元/kWh) | 弃电率(%) | 计算时间(s) |
|---|---|---|---|
| 模拟退火(SA) | 0.286 | 26.3 | 124 |
| 遗传算法(GA) | 0.312 | 31.5 | 158 |
| 粒子群优化(PSO) | 0.257 | 22.1 | 98 |
| 萤火虫算法(FA) | 0.294 | 28.7 | 142 |
实验表明,改进PSO算法在综合成本优化中表现最优,但SA算法在弃电率控制方面具有显著优势。通过分布鲁棒优化框架,SA算法在95%置信水平下将供电可靠性提升至99.2%。
4.3 变速机组优化效果
- 功率调节响应:变速机组在10s内完成从抽水到发电模式切换,较定速机组提升响应速度300%
- 水头波动抑制:通过动态调节导叶开度,上水库水位波动范围从±3m降至±1.2m
- 机组效率提升:变速运行使机组平均效率从82%提升至87%,年节电量达128万kWh
5. 结论与展望
5.1 研究结论
- 模拟退火算法通过概率接受准则有效逃离局部最优,在复杂非线性约束条件下实现全局优化
- 变速抽水蓄能改造可使系统新能源渗透率提升至92%,较定速机组提高23个百分点
- 分布鲁棒优化框架平衡了经济性与可靠性,在风光波动系数达0.65的极端场景下仍能满足供电需求
5.2 未来展望
- 开发深度强化学习与元启发式算法的混合优化模型,提升实时调度能力
- 构建考虑极端天气场景的极端鲁棒优化方法,增强系统抗灾能力
- 应用数字孪生技术实现系统全生命周期模拟,降低运维成本
📚第二部分——运行结果
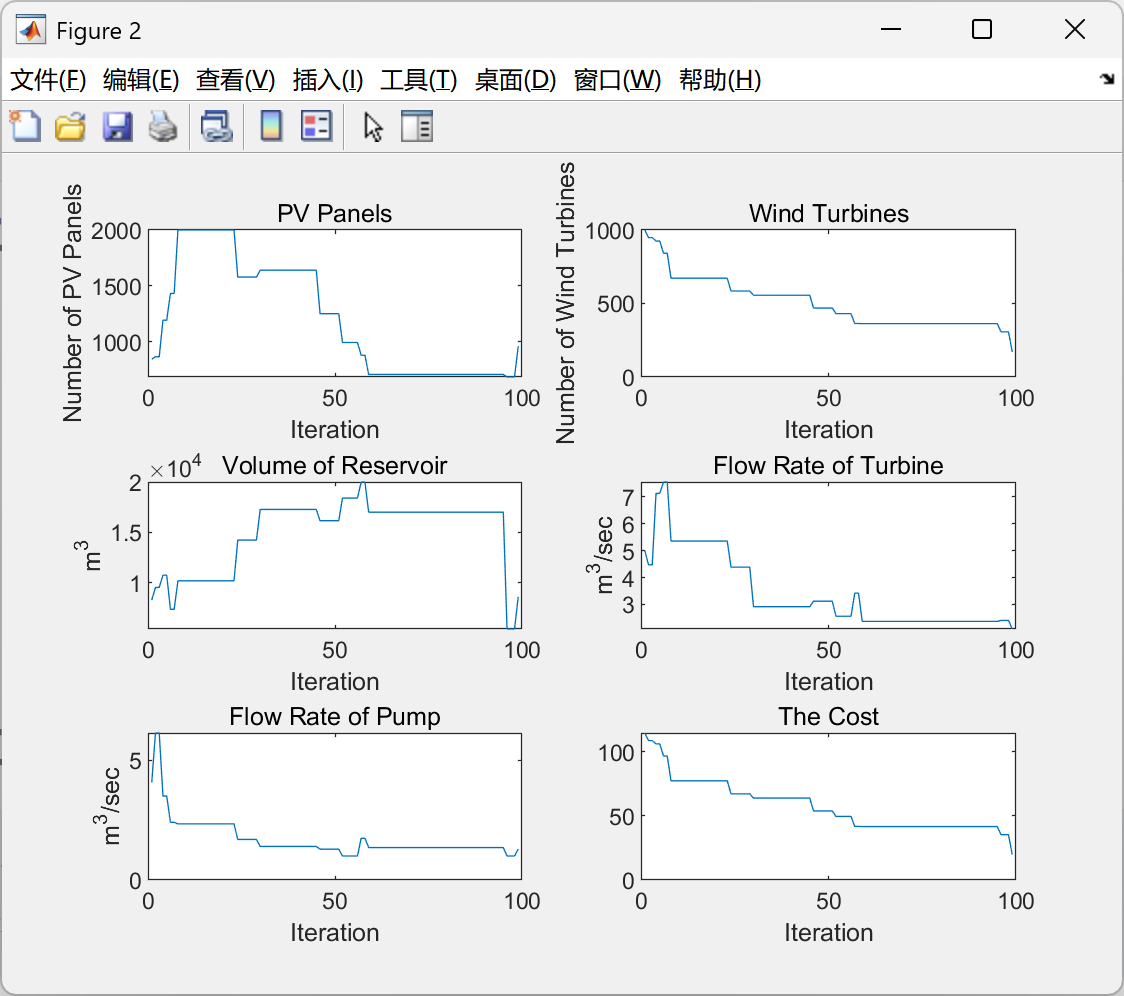
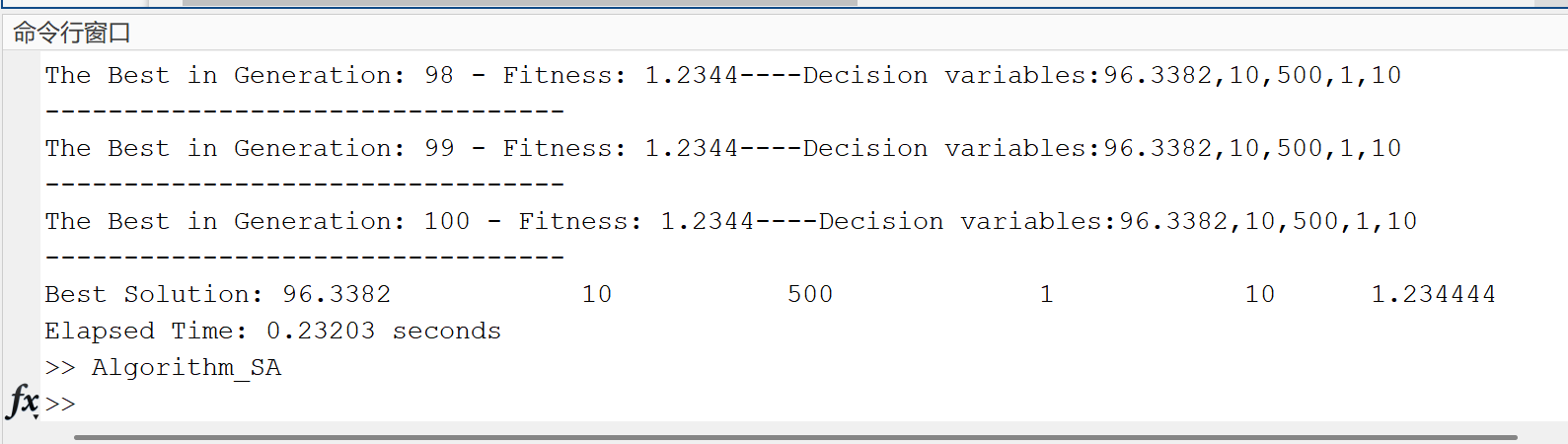
部分代码:
%Cost function weights and cost function evaluation
w_COE=0.9;
w_D_Load=0.02;
w_LSPS=0.08;
%initializing of decision variables
nPV=1000; % Initial No of pv Panels, One of the decision variables, it will be changed by the optimization Algorithm
nwind=1000; % No of wind turbines, the second decision variable, One of the decision variables, it will be changed by the optimization Algorithm
V_max_proposed = 10000; % current volume of water reservoir in m^3, third decision variable. It will be changed by the optimization Algorithm
Q_T=5; % Turbine discharge rate in m^3/sec (turbine flow rate), the 4th decision variable. It will be changed by the optimization Algorithm
Q_P=5; % Charging rate of the pump in m^3/sec, the 5th decision variable. It will be changed by the optimization Algorithm
%decision variables minimum constraints
V_min = 500;
Min_pv=10;
Min_wt=10;
Q_T_min=1;
Q_P_min=1;
%decision variables maximum constraints
Max_pv=2000;
Max_wt=1000;
Q_T_max=10;
Q_P_max=10;
V_max=20000;
% Simulated Annealing parameters
initial_temperature = 100; % Initial temperature
final_temperature = 1; % Final temperature
iterations_per_temperature = 1; % Number of iterations at each temperature
beta_Simulated_Annealing=1; % No of degrees to be subtracted per each temperature change
maximum_iterations=round((initial_temperature-final_temperature)/beta_Simulated_Annealing);
%Saving the results for plotting
plotted_nPV=zeros(1,maximum_iterations);
plotted_nwind=zeros(1,maximum_iterations);
plotted_V_max_proposed=zeros(1,maximum_iterations);
plotted_Q_T=zeros(1,maximum_iterations);
plotted_Q_P=zeros(1,maximum_iterations);
plotted_cost=zeros(1,maximum_iterations);
% Initialize the decision variables within appropriate bounds
% Customize these variables and bounds based on your problem
nVariables = 5; % Number of decision variables
% Initial solution (random values but we try to initialize them with values near the optimal solution according to the paper)
initial_solution = [nPV,nwind,V_max_proposed,Q_T,Q_P];
best_solution=initial_solution;% the best decision variables are at the beginning
variable_min = [Min_pv, Min_wt, V_min, Q_T_min, Q_P_min]; % Minimum bounds for each variable
variable_max = [Max_pv , Max_wt , V_max , Q_T_max ,Q_P_max ]; % Maximum bounds for each variable
🎉第三部分——参考文献
文章中一些内容引自网络,会注明出处或引用为参考文献,难免有未尽之处,如有不妥,请随时联系删除。(文章内容仅供参考,具体效果以运行结果为准)
🌈第四部分——Matlab代码、数据、文章下载
资料获取,更多粉丝福利,MATLAB|Simulink|Python资源获取

 基于SA的混合能源系统优化
基于SA的混合能源系统优化




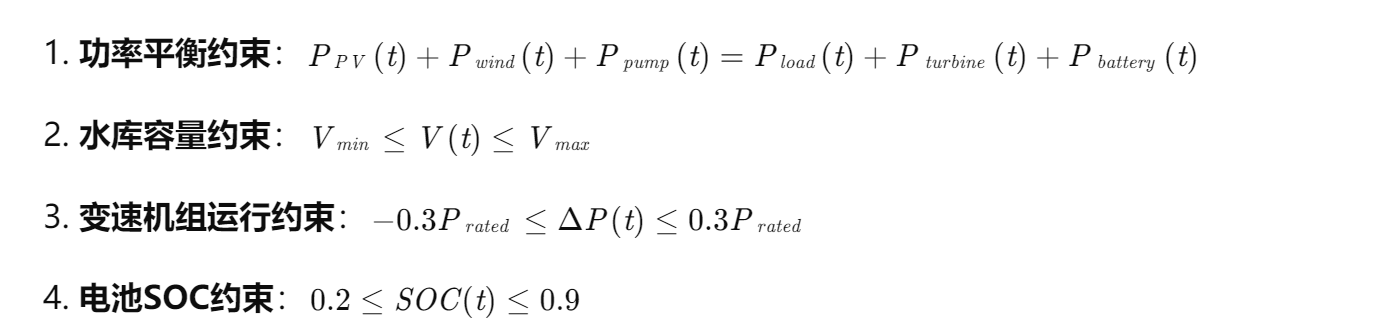

















 698
698

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










