目录
1.程序功能描述
本课题模型基于Stackelberg博弈理论,用于研究铁路物流中心中铁路运输企业与公路运输企业之间的定价策略和利益协同问题。
2.测试软件版本以及运行结果展示
MATLAB2022A/MATLAB2024B版本运行
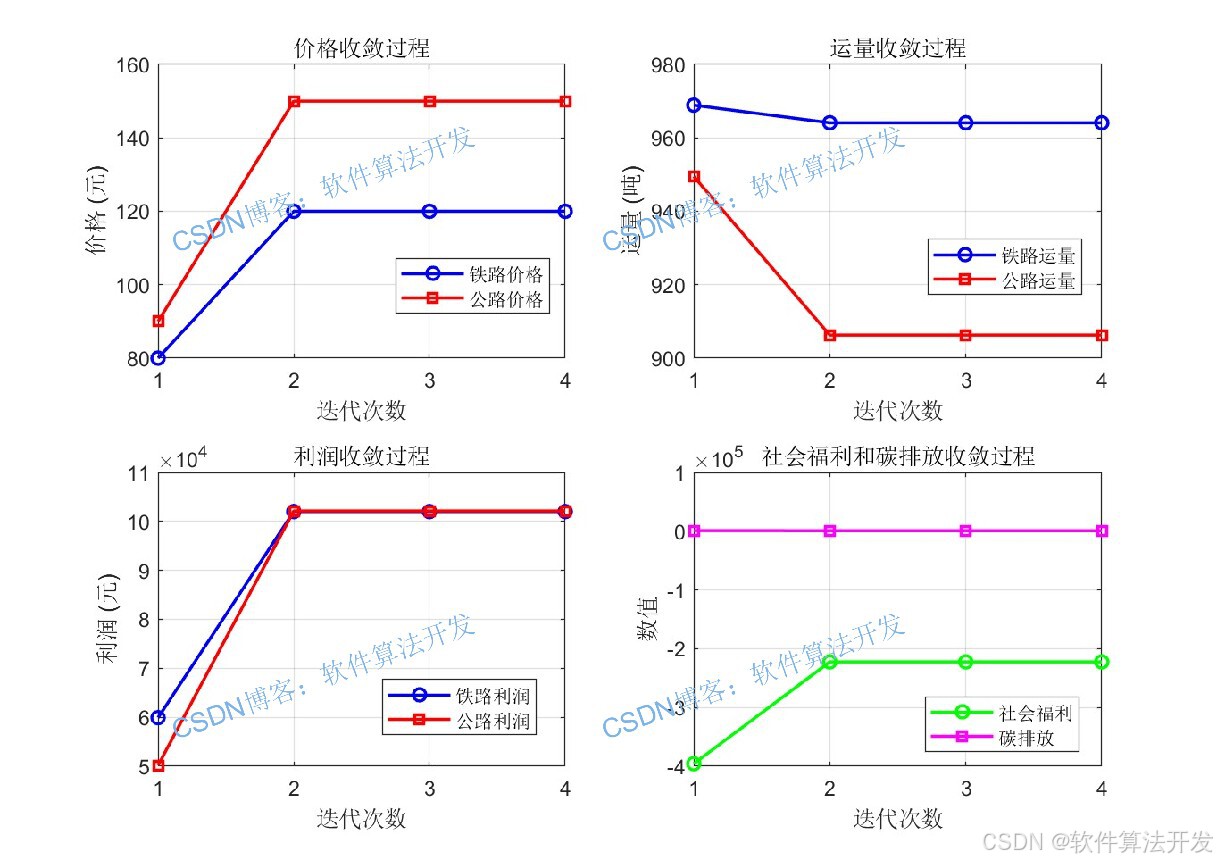
3.核心程序
.........................................
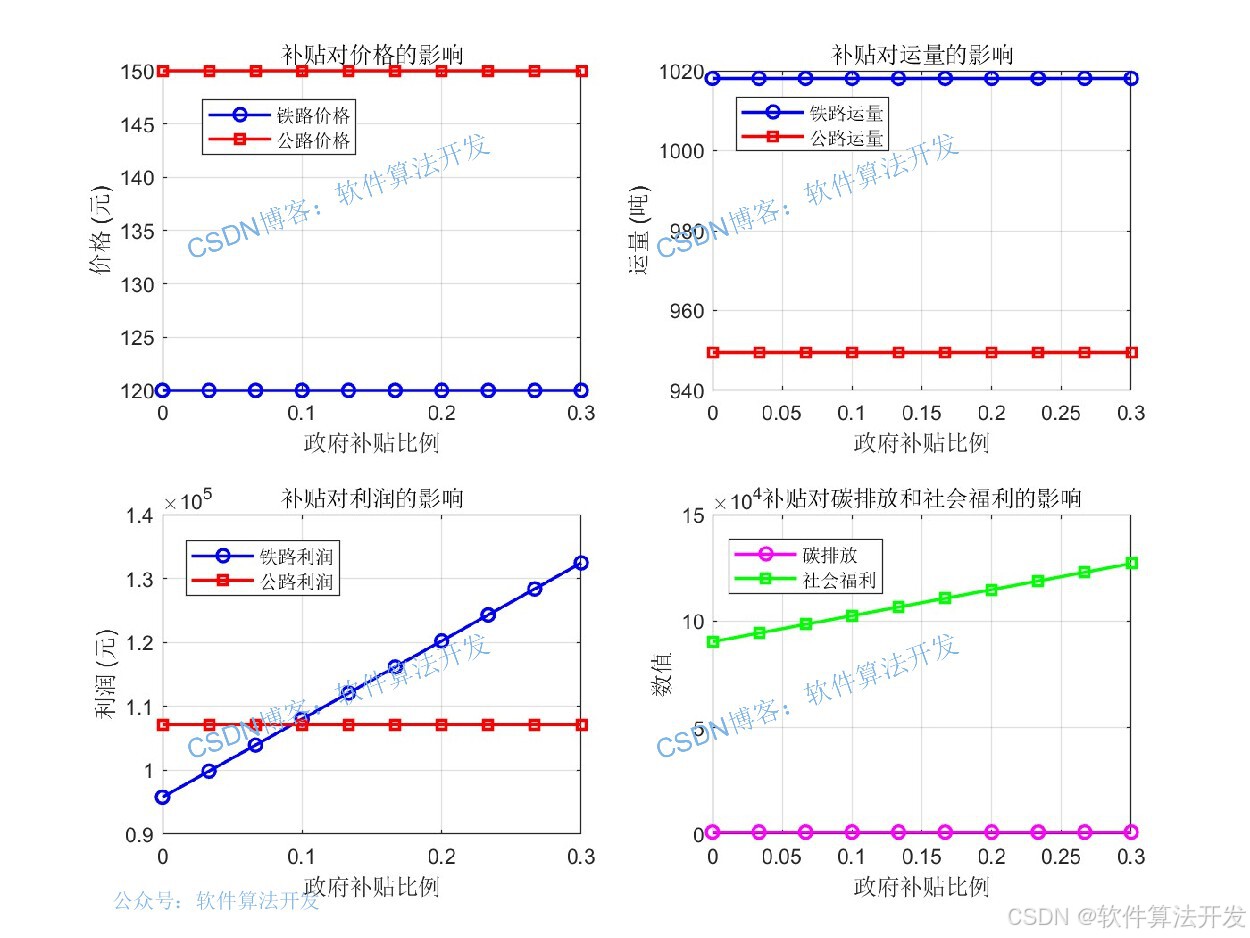
% 补贴影响分析图
figure('Position', [100, 100, 800, 600]);
subplot(2, 2, 1);
plot(subsidy_range, subsidy_results(:,1), 'b-o', 'LineWidth', 1.5);
hold on;
plot(subsidy_range, subsidy_results(:,2), 'r-s', 'LineWidth', 1.5);
grid on;
xlabel('补贴比例');
ylabel('价格 (元)');
title('补贴对价格的影响');
legend('铁路价格', '公路价格');
set(gca, 'FontSize', 10);
subplot(2, 2, 2);
plot(subsidy_range, subsidy_results(:,3), 'b-o', 'LineWidth', 1.5);
hold on;
plot(subsidy_range, subsidy_results(:,4), 'r-s', 'LineWidth', 1.5);
grid on;
xlabel('补贴比例');
ylabel('运量 (吨)');
title('补贴对运量的影响');
legend('铁路运量', '公路运量');
set(gca, 'FontSize', 10);
subplot(2, 2, 3);
plot(subsidy_range, subsidy_results(:,5), 'b-o', 'LineWidth', 1.5);
hold on;
plot(subsidy_range, subsidy_results(:,6), 'r-s', 'LineWidth', 1.5);
grid on;
xlabel('补贴比例');
ylabel('利润 (元)');
title('补贴对利润的影响');
legend('铁路利润', '公路利润');
set(gca, 'FontSize', 10);
subplot(2, 2, 4);
plot(subsidy_range, subsidy_results(:,7), 'm-o', 'LineWidth', 1.5);
hold on;
plot(subsidy_range, subsidy_results(:,8), 'g-s', 'LineWidth', 1.5);
grid on;
xlabel('补贴比例');
ylabel('数值');
title('补贴对碳排放和社会福利的影响');
legend('碳排放', '社会福利');
set(gca, 'FontSize', 10);
% 输出详细的指标结果
fprintf('\n敏感性分析结果:\n');
fprintf('------------------------\n');
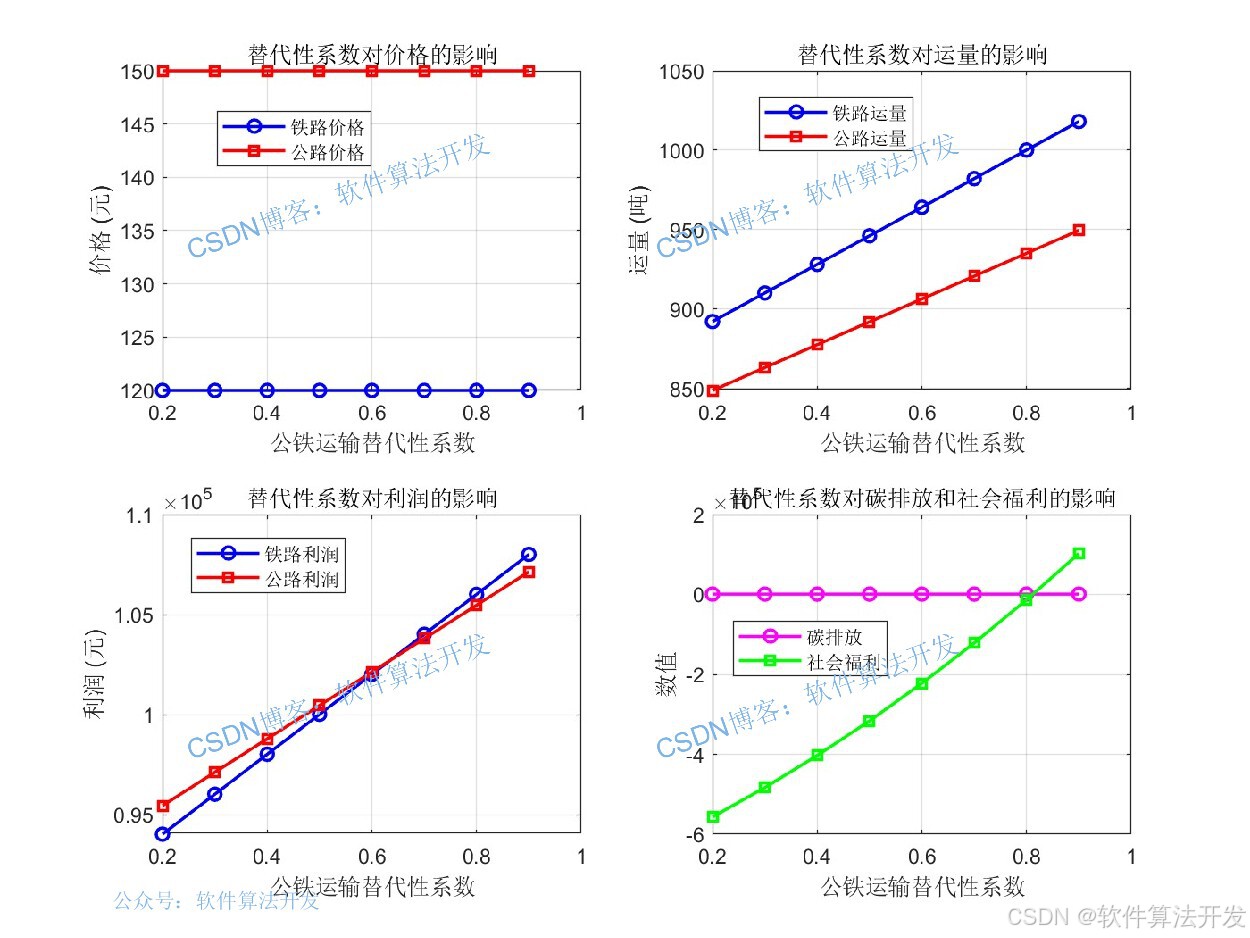
fprintf('\n不同替代性系数下的结果:\n');
fprintf('替代性系数\t铁路价格\t公路价格\t铁路运量\t公路运量\t铁路利润\t公路利润\t碳排放\t社会福利\n');
for i = 1:length(gamma_range)
fprintf('%.2f\t\t%.2f\t\t%.2f\t\t%.2f\t\t%.2f\t\t%.2f\t\t%.2f\t\t%.2f\t%.2f\n', ...
gamma_range(i), subsidy_results(i,1), subsidy_results(i,2), subsidy_results(i,3), ...
subsidy_results(i,4), subsidy_results(i,5), subsidy_results(i,6), subsidy_results(i,7), subsidy_results(i,8));
end
fprintf('\n不同补贴比例下的结果:\n');
fprintf('补贴比例\t铁路价格\t公路价格\t铁路运量\t公路运量\t铁路利润\t公路利润\t碳排放\t社会福利\n');
for i = 1:length(subsidy_range)
fprintf('%.2f\t\t%.2f\t\t%.2f\t\t%.2f\t\t%.2f\t\t%.2f\t\t%.2f\t\t%.2f\t%.2f\n', ...
subsidy_range(i), subsidy_results(i,1), subsidy_results(i,2), subsidy_results(i,3), ...
subsidy_results(i,4), subsidy_results(i,5), subsidy_results(i,6), subsidy_results(i,7), subsidy_results(i,8));
end
06_100m4.算法仿真参数
% 市场基本参数
a = 1000; % 市场潜在需求规模
b = 1.2; % 价格敏感度系数
gamma = 0.7; % 公铁运输替代性系数(0-1之间)% 成本参数
c_r = 20; % 铁路单位运输成本
c_r_fixed = 5000; % 铁路固定运营成本
c_t = 30; % 公路单位运输成本
c_t_fixed = 3000; % 公路固定运营成本% 服务质量参数
k_r = 0.8; % 铁路服务质量系数
k_t = 0.6; % 公路服务质量系数
delta = 0.5; % 服务质量对需求的影响系数% 碳排放参数
e_r = 0.2; % 铁路单位运输碳排放量(kg/吨·公里)
e_t = 0.8; % 公路单位运输碳排放量(kg/吨·公里)
carbon_price = 5; % 碳排放价格(元/kg)% 补贴参数
subsidy_rate = 0.1; % 对铁路运输的补贴比例% 价格上限约束
p_r_max = 120; % 铁路运输最高价格
p_t_max = 150; % 公路运输最高价格% 博弈迭代参数
max_iter = 100; % 最大迭代次数
tolerance = 1e-6; % 收敛容差
%% Stackelberg博弈求解
% 初始化价格
p_r = 80; % 铁路初始价格
p_t = 90; % 公路初始价格
5.算法理论概述
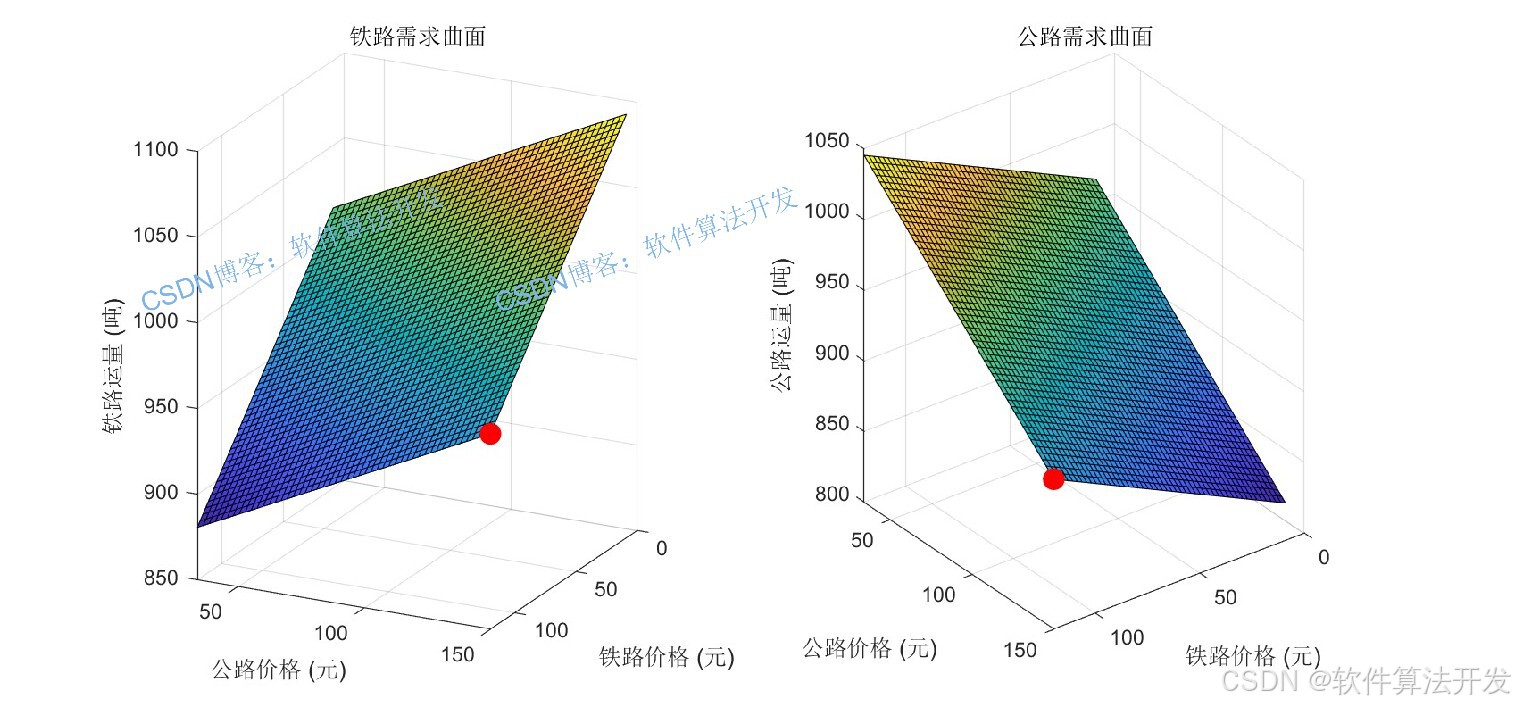
模型中使用的需求函数基于线性需求理论,考虑了价格和服务质量对需求的影响:
铁路运输需求函数:
qr=a−b⋅pr+γ⋅b⋅pt+δ⋅(kr−kt)
公路运输需求函数:
qt=a−b⋅pt+γ⋅b⋅pr+δ⋅(kt−kr)
其中:
qr和qt分别为铁路和公路的运输量
pr和pt分别为铁路和公路的运输价格
a表示市场潜在需求规模
b表示价格敏感度系数
γ表示公铁运输替代性系数 (0-1 之间)
kr和kt分别为铁路和公路的服务质量系数
δ表示服务质量对需求的影响系数
成本与利润函数:



Stackelberg博弈原理
Stackelberg博弈是一种序贯博弈,其中有一个领导者 (Leader) 和一个或多个跟随者 (Follower)。在本模型中:
铁路运输企业作为领导者,首先制定价格 pr
公路运输企业作为跟随者,观察到铁路价格后制定自己的价格 pt
博弈的求解过程是逆向归纳法:
首先求解公路企业的最优反应函数 pt∗(pr)
然后铁路企业在考虑公路企业反应的情况下,求解自己的最优价格 pr∗
6.参考文献
[1]王庆利,王丹,井元伟,等.激励Stackelberg策略下的电价算法[J].东北大学学报:自然科学版, 2006, 27(1):4.DOI:10.3321/j.issn:1005-3026.2006.01.001.
[2]程杉,陈欢田.基于Stackelberg博弈的智能电网完全分布式需求响应策略[J].陕西电力, 2019, 047(003):60-65,96.
7.完整程序
VVV
























 1104
1104

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










