力扣 第 284 场周赛 2203. 得到要求路径的最小带权子图

 

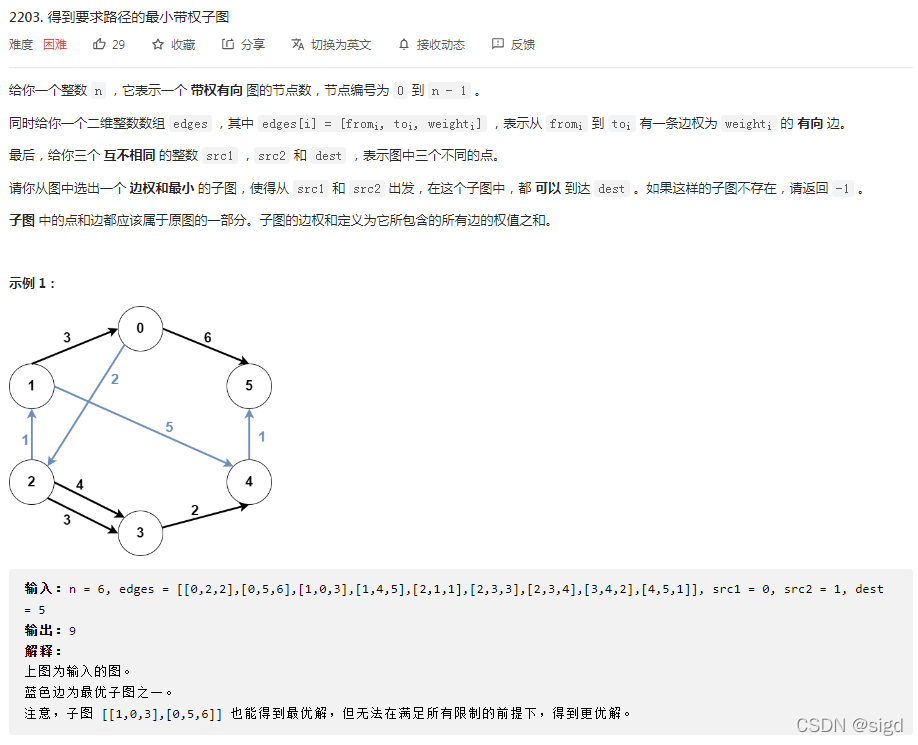
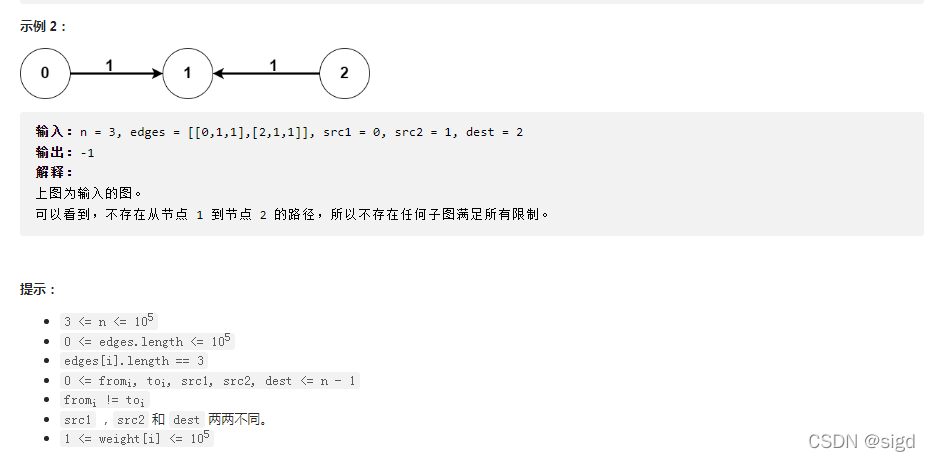
解题思路：这个题思路相对简单，考察优化的迪杰斯塔拉算法。

题意s1和s2存在到dest的路径，而且又要子图权值最小。
先介绍一个知识点，在有向图求多个点s1...sx到一个点d的最短路径时，解决方式是将图结构反向存储，然后求d到其他点最短路径。
当然，我们并不需要求出dest到s1和s2的最短路径和，因为很容易证明这个和不是答案，因为可能存在公共边，公共边不需要计算两次。这些公共边构成了“公共路径”，这条公共路径终点必然是dest，起点不确定。
实际上通过模拟可以知道，公共路径起点可以是任意一个点，包括（src1，src2，dest）。
因此，枚举这个公共路径起点，假设它为X，这样答案就是:src1到X最短距离+src1到X最短距离+X到dest最短距离。
因此做三次最短路径算法，其中src1和src2的最短路径用原图，X到dest的最短路径将图反向存储，再求dest到其他点最短路径。

因为此题目数据比较大，一旦不开longlong的结果就是无情的WA（我中招了）。

class Solution {
public:
    struct node
    {
        long long adj,v;/**< 习惯性用结构体，其实用pair就行 */
        bool operator <(const node B)const
        {
            return v>B.v;
        }
    };
    void getPath(int n, vector<node >e[], int s, long long d[])
    {
        priority_queue<node>pq;/**< 优先队列找到最短路径 */
        int i,j;
        for(i=0;i<n;i++)
            d[i]=20000000000,pq.push({i,20000000000});
        d[s]=0;
        pq.push({s,0});
        for(j=1;j<n;j++)
        {
            int now=pq.top().adj;
            pq.pop();
            for(i=0;i<e[now].size();i++)
            {
                int y=e[now][i].adj,z=e[now][i].v;
                if(d[y]>d[now]+z)
                    d[y]=d[now]+z,pq.push({y,d[y]});
            }
        }
    }
    long long minimumWeight(int n, vector<vector<int> >& edges, int src1, int src2, int dest) {
        long long i,j,s1[100005],s2[100005],d[100005],ans=30000000000;
        vector<node > e [n+1],e2[n+1];
        for(i=0;i<edges.size();i++ )
        {
            e[edges[i][0]].push_back({edges[i][1],edges[i][2]});
            e2[edges[i][1]].push_back({edges[i][0],edges[i][2]});
        }
        getPath(n,e,src1,s1);
        getPath(n,e,src2,s2);
        getPath(n,e2,dest,d);/**< 求dest时用反向图结构 */
      for(i=0;i<n;i++)
         ans=min(ans,d[i]+s1[i]+s2[i]);
      if(ans>=20000000000)
          ans=-1;
      return ans;
    }
};