小苯的区间删除-2024年淘天集团春招研发岗笔试

解题思路：删除区间后剩余的部分合并是有序。可以将剩余的区间分为左半段和右半段。左半段有序且最大值a[i]小于右半段最小值a[j]。

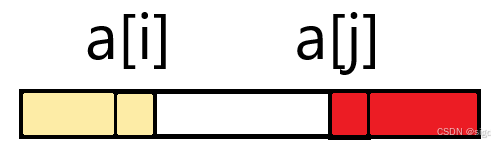
那么如何确定i和j的位置呢？

此类问题的解题思路一定是采用枚举法，枚举左区间i，计算右区间j的位置。

i的位置从左侧循环枚举，从0开始哦，（枚举i的过程中，一旦不满足升序，那么后面不会有符合条件左区间，可以结束枚举），当确定升序左区间[0,i]之后，可以从n+1开始由后向前确定j的位置，（同理，必须是降序向左侧前进，一旦不是降序，也就不用前进了）。

降低复杂度的思路：后一次用前一次的结果，当计算完a[i]之后，枚举符合条件的a[i+1]时，可以使用上一次计算得到的j。具体做法参看代码。

时间复杂度：枚举i=0时确定一个右区间端点j，此后随着i不断增大，j的值也只能向后移动，所以算法的时间复杂度为O（n）.

#include <iostream>
using namespace std;
int n,a[200005];
long long ans=0;
int main()
{
    int i,j;
    cin>>n;
    for(i=1; i<=n; i++)
        cin>>a[i];
    a[n+1]=1e9+1;/**< 增加两个边界点a[0]=0<a[1],a[n+1]>a[n],方便处理 */
    j=n+1;
    for(i=0; i<=n; i++) /**< i为左区间最后一个结点,为什么是0开始，因为删除可以从头开始删除 */
    {
        if(i>0&&a[i]<a[i-1]) break;/**< 当[0,i]这个左区间无法升序时结束循环 */
        if(a[j]>=a[i]&&j>i) /**< 向左前进，找到比a[i]大的a[j],注意a[j]<=a[j+1] */
        {
            while(a[j-1]>=a[i]&&a[j]>=a[j-1]&&j-1>i)
                j--;
        }
        else  /**< 向右前进，因为右侧有序，调用二分查找找到第一个大于等于a[i]的a[j] */
            j=lower_bound(a+j+1,a+n+2,a[i])-a;
        ans+=n+2-j;/**< 为什么是n+2-j呢，因为当[1,i] 和[j,n]满足条件式，删除可能性[i+1,j-1]
         [i+1,j]......[i+1,n],正好是n-(j-2)*/
        if(j==i+1) ans--;/**< 当这个条件满足时,i+1就是j，那么上面那个计算次数会少一次 */
    }
    cout<<ans;
    return 0;
}