一文看懂 LQR 算法：让自动驾驶小车 “聪明转弯” 的最优控制方案

原创于 2025-11-23 19:23:04 发布 · 645 阅读

CC 4.0 BY-SA版权

文章标签：

如果你已经学过 Stanley 或 PurePursuit 算法，可能会发现一个特点：它们都是 “哪里偏了补哪里” 的几何跟踪方法 —— 看到小车离路径远了、方向歪了，再调整方向盘。但如果想让小车 “更聪明”，比如提前考虑 “车身惯性”“转弯力度”，避免猛打方向盘或晃荡，那LQR（线性二次调节器） 就是更合适的选择。

LQR 是自动驾驶路径跟踪里 “基于模型的最优控制” 入门款，核心逻辑很简单：先给小车画一张 “运动蓝图”（数学模型），再算一个 “又准又稳” 的控制方案—— 既让小车贴紧路径，又不让控制动作太激烈。哪怕你刚接触 “最优控制”，也能通过这篇文章搞懂它的核心思路。

一、先想明白：为什么需要 LQR？

在学 LQR 之前，先回顾下之前的算法问题：Stanley 和 PurePursuit 都不怎么考虑小车的 “物理特性”。比如：

小车有惯性，猛打方向盘会晃；
转向电机有最大转角，不能转太狠；
高速和低速时，小车的反应完全不一样。

而 LQR 的优势就在于：它会先 “摸清小车的脾气”（建立运动模型），再根据模型算 “最优的控制动作”—— 不是 “粗暴纠正偏差”，而是 “优雅地引导小车回到路径”。

举个生活化的例子：

Stanley/PurePursuit 像 “新手开车”：看到偏了就猛打方向，修正过头了再往回打，容易晃；
LQR 像 “老司机开车”：提前预判车身惯性，轻轻打方向，既不跑偏又平稳。

二、LQR 的核心：先建 “模型”，再找 “最优”

LQR 的逻辑分两步：先给小车建一个 “线性运动模型”（告诉算法小车怎么动），再定义一个 “代价函数”（告诉算法什么是 “好的控制”），最后算出让代价最小的控制方案。

1. 第一步：给小车建 “运动蓝图”—— 线性状态方程

小车的运动不是随心所欲的，比如 “打 10° 方向盘，小车会怎么拐”，是有物理规律的。LQR 会把这个规律写成一个线性状态方程（核心公式 1），这是 LQR 的 “基础”：

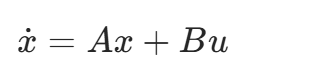
别被符号吓到，我们逐个拆成 “人话”，用小车最常用的 “自行车模型” 举例：

符号	含义（小车场景）	通俗解释
. x	状态变化率	小车 “下一步” 的状态变化（比如横向偏差会变大还是变小）
x	状态向量	描述小车 “当前情况” 的关键信息，比如：\(x = [横向偏差, 航向误差, 横向速度]\)（这三个量能反映小车是否跑偏、会不会继续跑偏）
A	状态矩阵	小车 “自身运动的规律”：比如横向偏差怎么影响后续的航向误差（由小车物理参数决定，如轴距、质量）
B	控制矩阵	控制动作对小车的影响：比如打方向盘（控制量）会让横向偏差怎么变
u	控制量	我们能给小车的指令：这里就是 “前轮转角”（和 Stanley、PurePursuit 的控制目标一样）

关键补充：为什么叫 “线性”？因为小车的真实运动是 “非线性” 的（比如大转角时，运动规律不是直线关系），但 LQR 会把它 “近似成线性”（比如在 “接近路径” 的小范围内，运动规律接近直线），这样才能用上面的方程计算 —— 这就是 “线性化”，是 LQR 的核心前提，但不用你手动算，仿真工具（如 Python 的 scipy）能帮你搞定。

2. 第二步：定义 “好控制” 的标准 —— 代价函数

有了模型，LQR 还需要知道 “什么样的控制是好的”。比如：

希望小车离路径越近越好（横向偏差小）；
希望方向盘别猛打（转角变化小，避免晃荡）；
这两个目标可能冲突（比如为了快速纠偏，不得不猛打方向），需要 “权衡”。

LQR 用二次型代价函数（核心公式 2）来量化这个标准，目标是让这个函数的值最小：

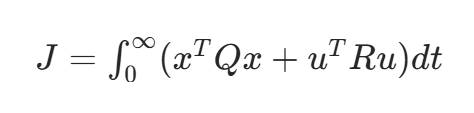
同样拆成 “人话”：

符号	含义	通俗解释
J	总代价	代价越小，控制效果越好
x^TQx	状态代价	衡量 “跑偏的严重程度”：Q是 “权重矩阵”，你想让 “横向偏差” 更重要，就把Q里对应 “横向偏差” 的位置设大一点（比如设 10）；想让 “航向误差” 没那么重要，就设小一点（比如设 1）
u^TRu	控制代价	衡量 “控制动作的激烈程度”：R是 “控制权重矩阵”，你想让方向盘别猛打，就把R设大一点（比如设 5）；如果允许激烈调整，就设小一点（比如设 1）
	积分	考虑 “整个过程” 的代价，不是只看某一瞬间

举个例子：如果你的小车是实验室的低速小车，怕晃荡，就把R设大（比如\(R=10\)），这样 LQR 会优先保证方向盘平缓；如果是高速小车，怕跑偏，就把Q里 “横向偏差” 的权重设大（比如设 20），优先保证贴紧路径。

3. 第三步：算出 “最优控制”—— 反馈增益 K

有了模型（\(\dot{x}=Ax+Bu\)）和代价标准（J），LQR 会通过求解一个叫 “黎卡提方程” 的数学方程（不用你手动解，工具能算），得到一个最优反馈增益矩阵 K，最后用下面的公式输出控制量（前轮转角）：

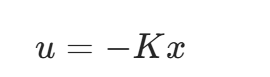
这是 LQR 的 “最终执行公式”，逻辑特别直接：

小车的当前状态x（比如横向偏差 2cm、航向误差 3°）乘以K，得到一个 “调整量”；
加个负号，意思是 “反向纠正”（比如横向偏差在左边，就输出右拐的转角）；
最终的u就是 “最优的前轮转角”，既纠正了偏差，又不会太激烈。

三、LQR 怎么 “工作”？三步循环

和 Stanley 的 “实时循环” 类似，LQR 在小车上运行时，也是每秒几十次重复下面三步，保证持续最优控制：

测状态：通过传感器（如 GPS、IMU、里程计）获取小车当前的状态x（横向偏差、航向误差、横向速度）；
算转角：把x代入\(u=-Kx\)，算出最优的前轮转角u（这里的K是提前通过黎卡提方程算好的，运行时不用再算）；
控小车：把转角u发给转向电机，小车执行后，进入下一次循环，重复 1-3 步。

关键区别：Stanley 是 “看到偏差再补偿”，而 LQR 是 “根据模型预判偏差变化，提前输出最优控制”—— 比如小车刚有点跑偏趋势，LQR 就已经算出 “最小力度的转角”，避免偏差变大。

四、LQR vs Stanley/PurePursuit：该选哪个？

作为新手，你可能会纠结 “学了几何算法，为什么还要学 LQR”。用一张表对比，你就清楚了：

对比维度	LQR 算法	Stanley/PurePursuit 算法
核心逻辑	基于模型的 “最优控制”（预判 + 权衡）	基于几何的 “偏差补偿”（哪里偏补哪里）
跟踪精度	更高（考虑小车动力学，不易跑偏）	稍低（低速 OK，高速易晃）
稳定性	更好（控制动作平缓，不易超调）	一般（可能因偏差大而猛打方向）
依赖条件	需小车模型（如轴距、质量）和线性化	无需模型（只需几何位置）
实现难度	中等（需理解模型和权重调节）	简单（只需算偏差）

新手建议：先在仿真里实现 LQR（不用真实小车模型），比如用 Python 的scipy.linalg.solve_continuous_are求解黎卡提方程，再和 Stanley 对比 —— 你会明显看到 LQR 的控制动作更平缓，跟踪精度更高，这就是 “最优控制” 的优势。

总结

LQR 的核心不是 “复杂的数学”，而是 “先懂小车，再做最优决策”—— 它不像 Stanley 那样 “见招拆招”，而是提前通过模型预判小车的运动，再用代价函数权衡 “精度” 和 “平稳”，最后输出最优控制。

如果你想从 “简单几何跟踪” 升级到 “基于模型的控制”，LQR 是必经之路。试着用仿真实现它，再和之前的算法对比，你会对自动驾驶的 “控制逻辑” 有更深的理解 —— 这不仅能帮你搞定小车实验，也能为后续学更复杂的 MPC 算法打下基础～