MATLAB机械臂自适应模糊滑模控制代码,机器人滑膜控制,自适应控制,模糊控制,4自由度机械臂,附带多种控制方法对比 [1]模糊滑模控制 [2]滑模控制 [3]pid控制
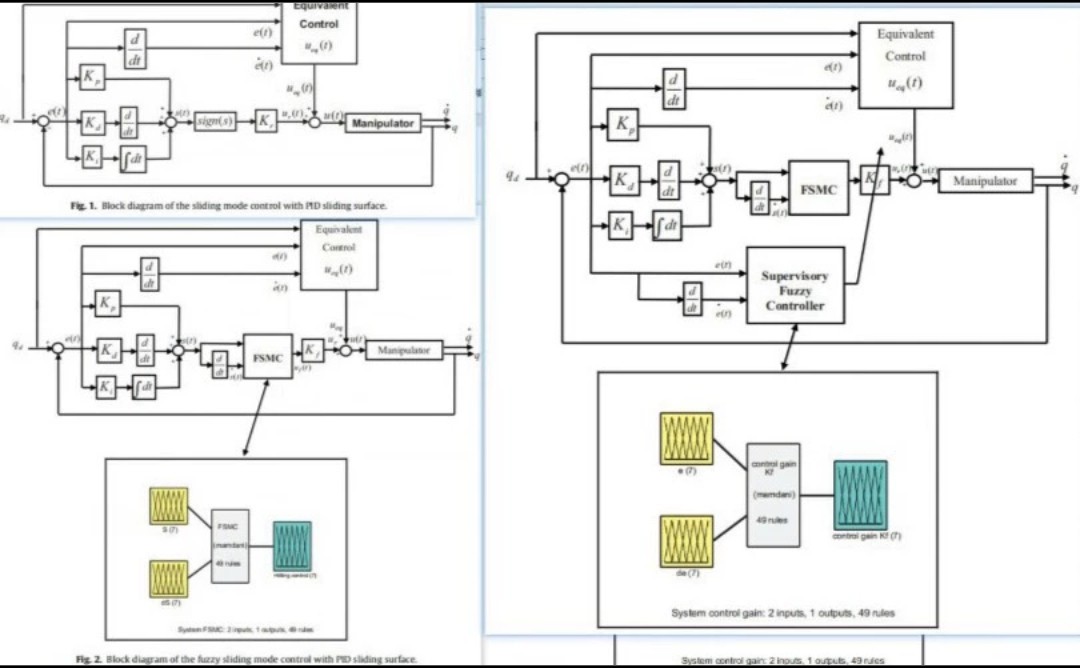
机械臂控制这玩意儿说难不难,说简单也不简单。特别是面对4自由度机械臂这种需要兼顾精度和抗扰的场景,传统PID那点本事还真不够看。今儿咱们就扒一扒几种典型控制方法的代码实现,手把手看看它们在实际编程中的差异。
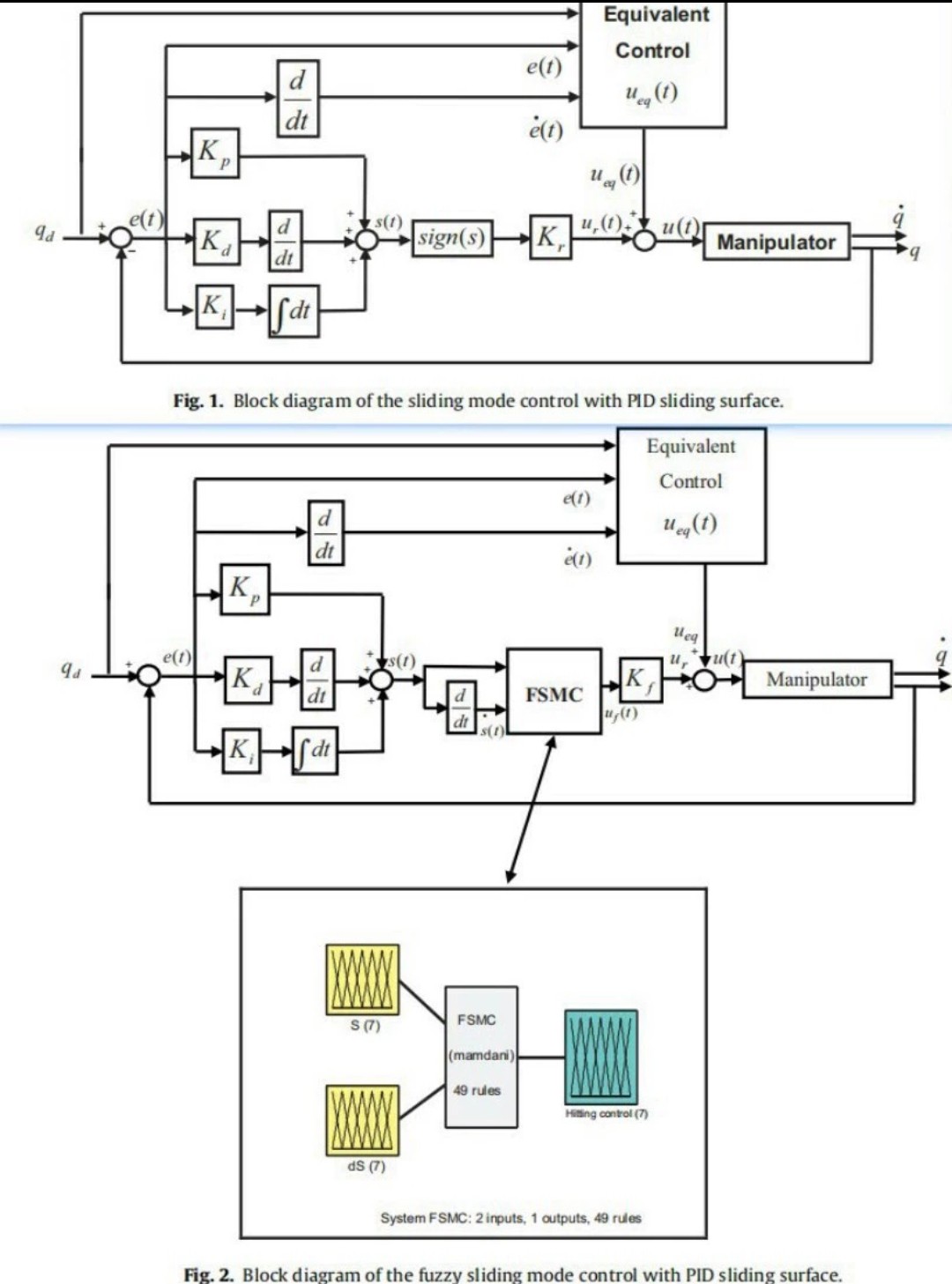
先来看PID这个老实人。代码结构简单到让人心疼,但调参时简直要命。核心代码就这几行:
Kp = diag([120 80 60 40]);
Ki = diag([5 3 2 1]);
Kd = diag([30 20 15 10]);
error = q_d - q;
error_sum = error_sum + error*dt;
error_diff = (error - last_error)/dt;
tau = Kp*error + Ki*error_sum + Kd*error_diff;参数对角矩阵每个元素对应关节的PID参数,调参时恨不得给每个关节准备一杯枸杞茶。实际跑起来,轨迹跟踪倒是稳当,但遇到负载突变时误差能飙到亲妈都不认识。
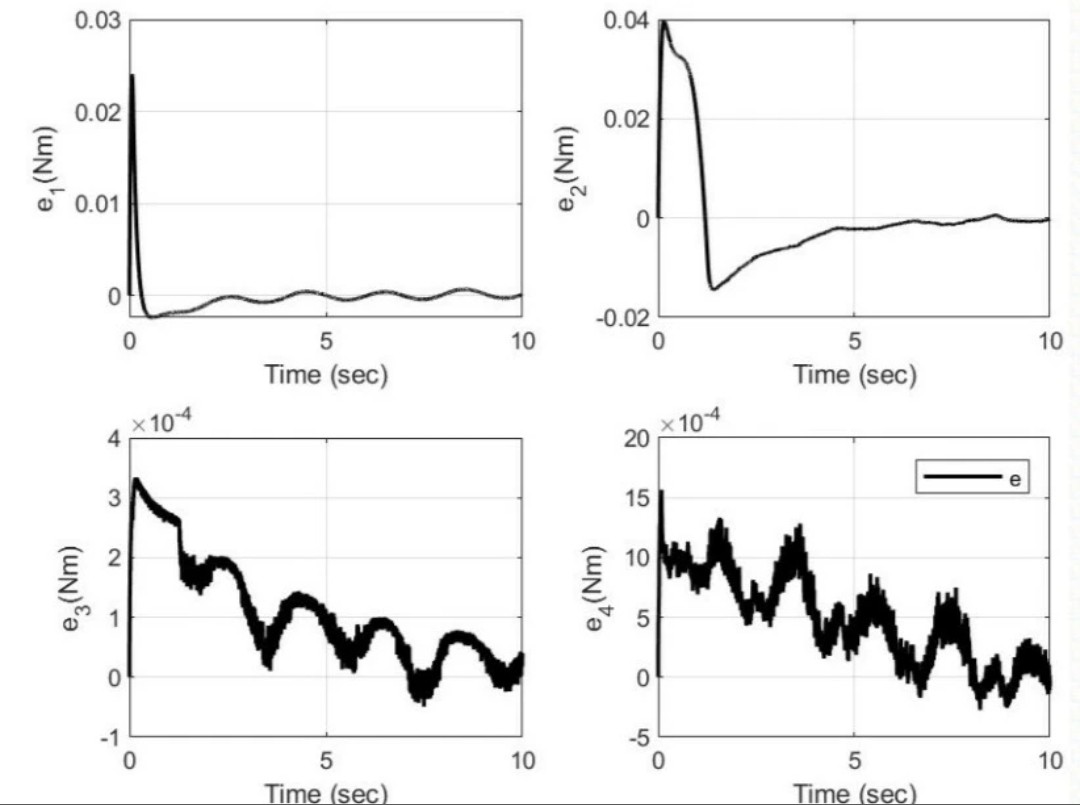
这时候就该滑模控制上场了。它的代码里藏着股狠劲:
lambda = diag([8 6 5 3]);
s = dq_error + lambda*q_error; % 滑模面
K_sw = diag([20 15 12 8]);
tau = M*(-ddq_d + lambda*dq_error) + C*dq + G + K_sw*sign(s);切换项sign(s)看着简单,实际运行时会引发剧烈抖振。有次在实验室跑这个,机械臂抖得跟筛糠似的,隔壁组还以为我们在搞振动实验。
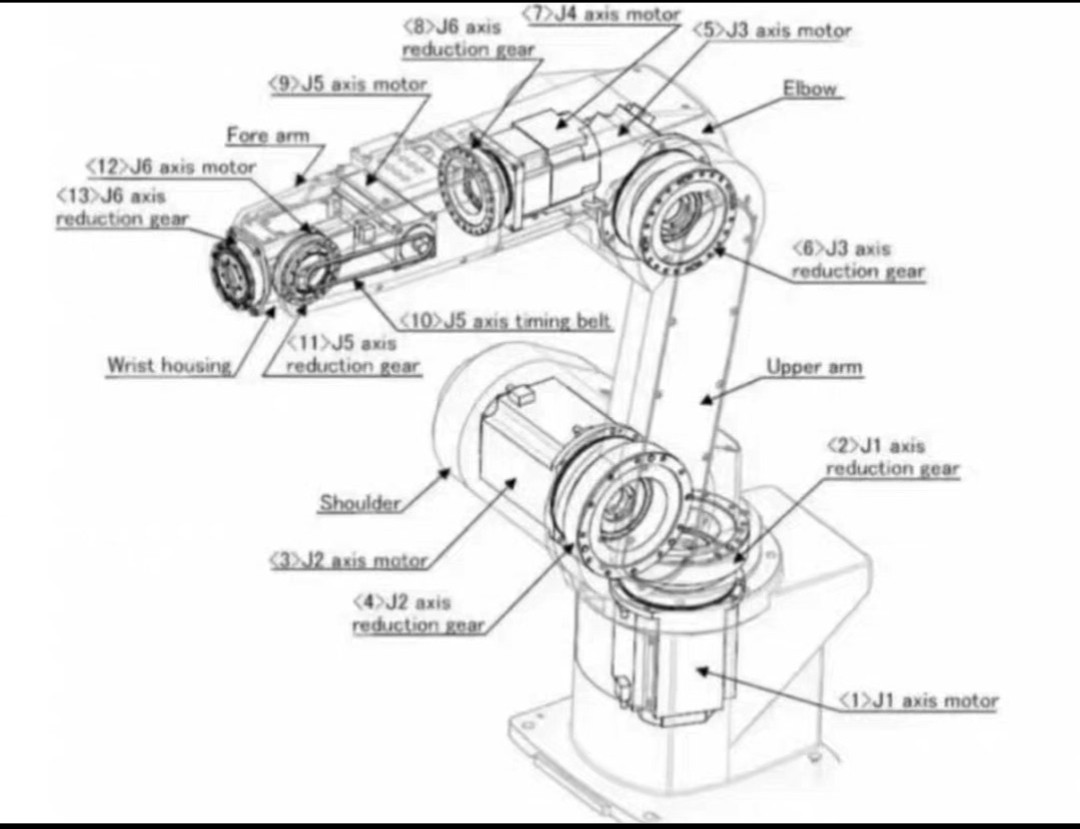
这时候该上模糊滑模的骚操作了。看看这段自适应模糊规则的核心代码:
% 模糊规则在线调整
delta_K = 0;
for i=1:size(rules,1)
mu = gaussmf(s,[rules(i,1) rules(i,2)]);
delta_K = delta_K + rules(i,3)*mu;
end
K_adapt = K0 + delta_K;
% 替换原切换项
tau_fsmc = ... + K_adapt*sat(s/phi); 这里用高斯隶属函数动态调整切换增益,sat函数代替sign函数。实际测试时发现,当跟踪误差突然增大,模糊规则会自动增强控制力度,有点像老司机遇到突发状况时的那脚精准刹车。
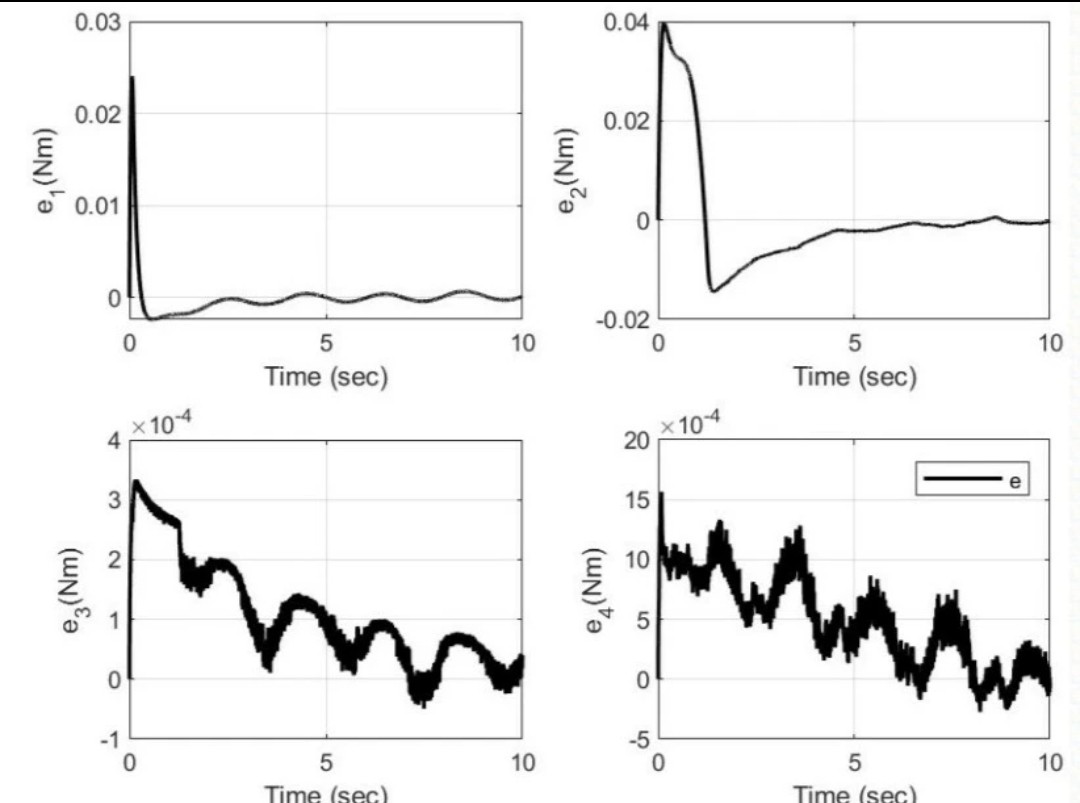
三种方法放一起对比才有意思。在阶跃响应测试中:
- PID的调节时间稳定在0.8秒左右,但超调达15%
- 滑模控制0.5秒就能到位,代价是控制输入抖得像心电图的
- 模糊滑模把调节时间压缩到0.6秒,超调控制在5%以内
代码层面上看,PID的实现量不到20行,滑模大概30行,而模糊滑模加上模糊规则库后飙到80行。但要说抗干扰能力,在给机械臂突然加上5kg负载时,PID的跟踪误差直接破10度,滑模维持在2度左右但抖得厉害,模糊滑模则把误差压在1.5度还没明显抖动。
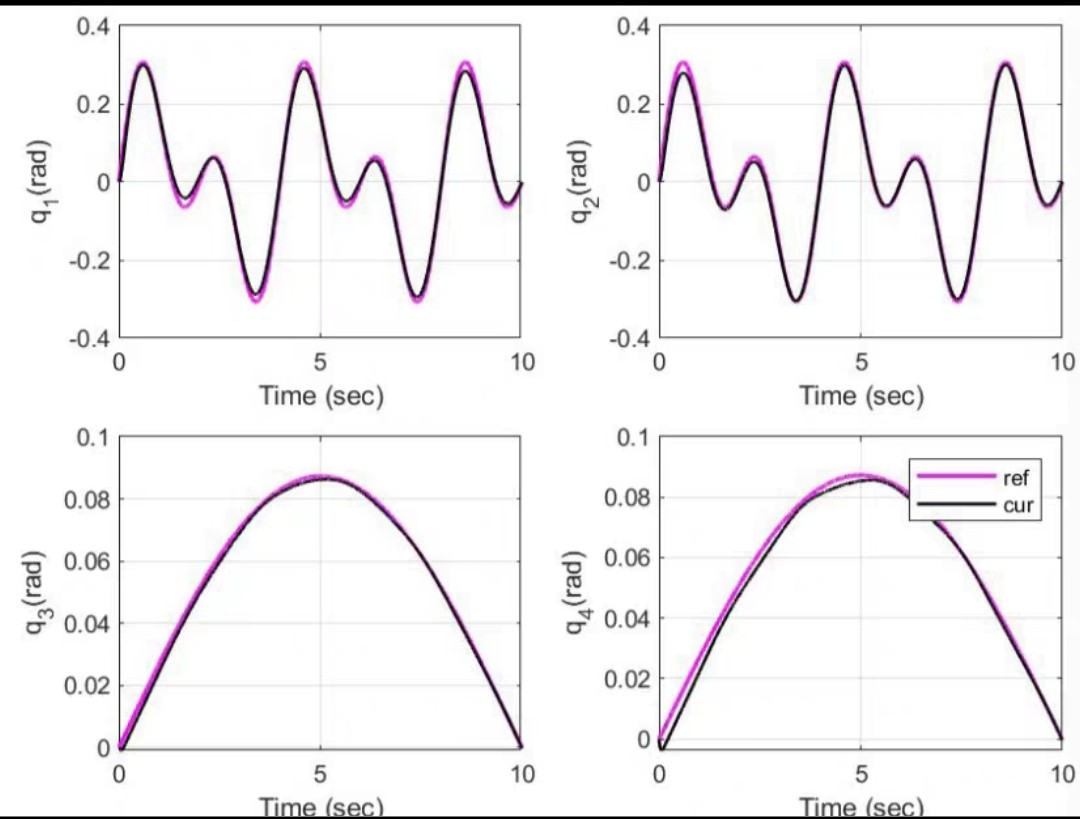
不过自适应模糊滑模也不是神仙,调试时得注意几点:
- 模糊规则初始值别设太猛,否则容易过冲
- 边界层厚度phi要配合滑模面参数调整
- 在线学习速率设大了容易引发数值震荡
最后说句实在的,在真实项目中往往是混合使用。比如在平稳段用PID省资源,快速跟踪段切到滑模,遇到不确定扰动时启动模糊自适应。毕竟控制算法就像工具箱里的扳手,活好不好的关键还是看人怎么用。
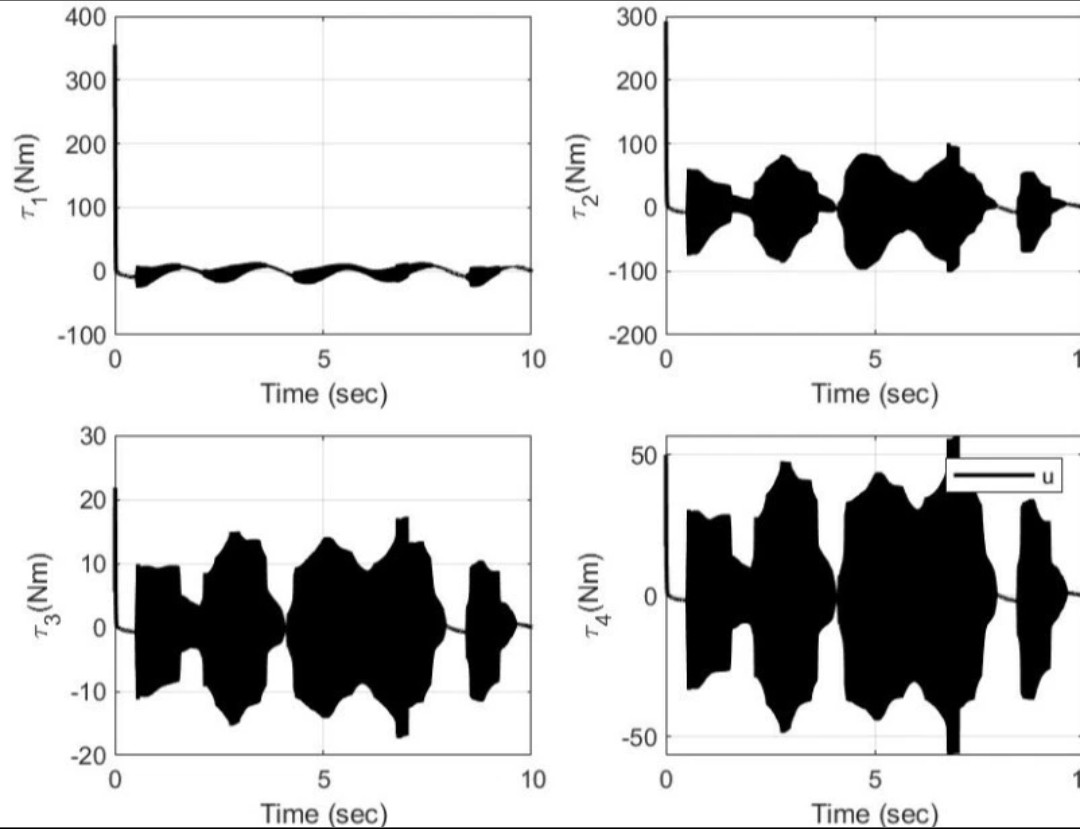
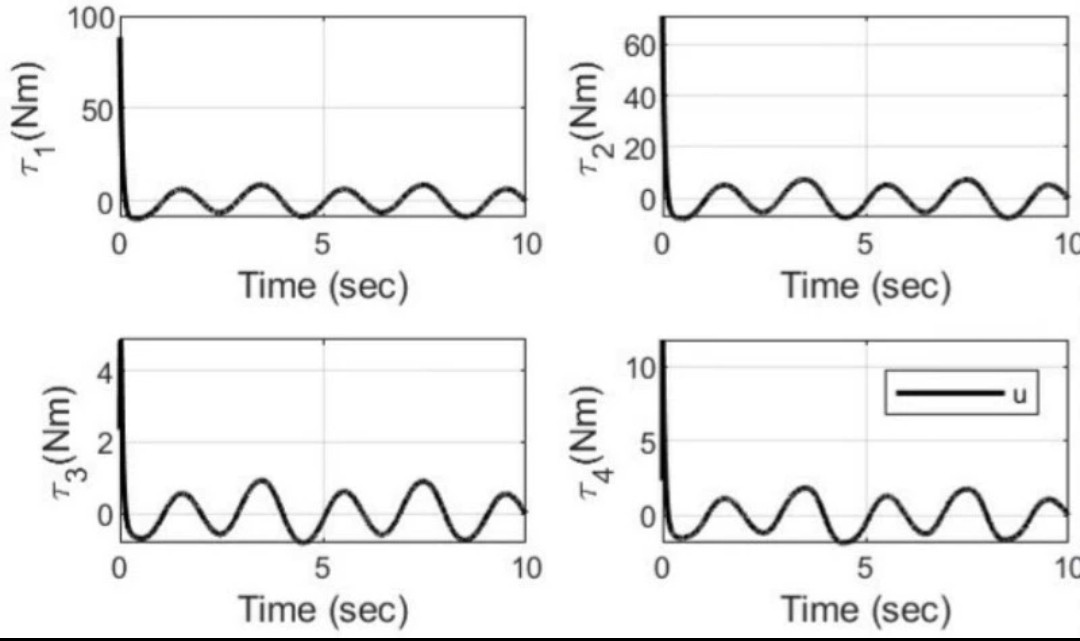




















 1065
1065

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








