1. 研究背景与意义
- 燃气轮机叶片的重要性:叶片是燃气轮机的核心部件,其加工质量直接决定发动机的效率、可靠性和寿命。
- N87耐热钢的材料特性:作为一种典型的镍基高温合金,N87具有优异的高温强度、抗蠕变和耐腐蚀性能。但正是这些特性导致其加工性极差,属于典型的难加工材料。具体问题包括:
- 加工硬化严重
- 切削力大、切削温度高
- 刀具磨损剧烈
- 加工表面质量难以控制
- 优化必要性:传统的“试错法”选择铣削参数成本高、效率低。通过科学的优化方法,寻找最优的铣削参数组合,对于提高加工效率、降低制造成本、保证加工质量(如表面粗糙度、形状精度)、延长刀具寿命具有重要意义。
2. 总体技术路线
本研究的核心思想是:
- 实验设计:通过设计实验,获取不同铣削参数下的多个性能指标数据。
- 多目标归一化:使用灰色关联分析 将多个优化目标(如表面粗糙度Ra、材料去除率MRR、切削力Fc)转化为一个单一的综合评价指标——灰色关联度。
- 非线性映射建模:使用径向基函数神经网络 建立从铣削参数到灰色关联度的精确非线性模型。
- 全局参数寻优:使用粒子群优化算法 在RBFNN模型上寻找使灰色关联度最大的铣削参数组合。
技术路线图:
实验设计 (DOE) → 数据采集 (Ra, MRR, Fc) → GRA多目标转化 → RBFNN模型训练与测试 → PSO在RBFNN模型空间寻优 → 获得最优参数组合并验证
3. 方法论详解
3.1 铣削参数与性能指标(优化目标)的确定
-
输入变量(铣削参数):
- 切削速度 (vc): m/min
- 进给量 (fz): mm/z
- 切削深度 (ap): mm
- (可选)径向切宽 (ae)
-
输出响应(性能指标):
- 表面粗糙度 (Ra): µm,代表加工质量,“望小特性”(越小越好)。
- 材料去除率 (MRR): cm³/min,代表加工效率,“望大特性”(越大越好)。
- 切削力 (Fc): N,代表加工载荷和能耗,也与刀具磨损有关,“望小特性”。
矛盾性:这些目标相互矛盾。例如,提高进给量可以增加MRR,但通常会导致Ra和Fc增大。因此,这是一个典型的多目标优化问题。
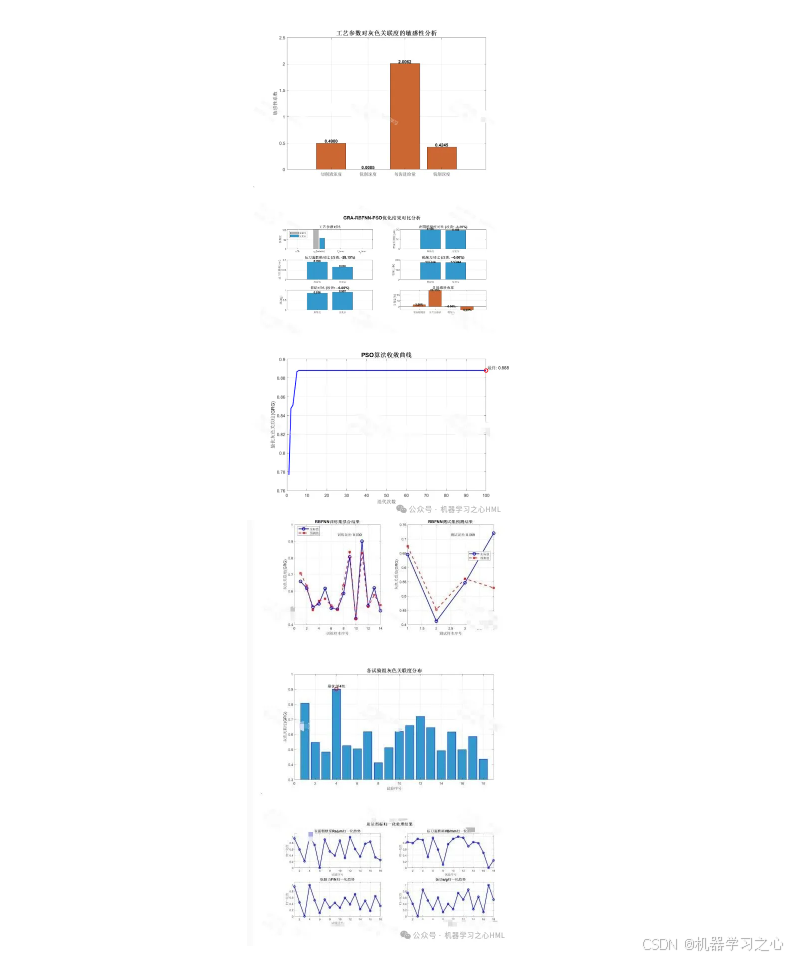
3.2 灰色关联分析 (GRA)
GRA用于解决多目标间的矛盾,将其转化为单目标优化问题。
-
数据预处理(归一化):
- 对于“望小特性”(Ra, Fc): ( x_i^*(k) = \frac{\max x_i(k) - x_i(k)}{\max x_i(k) - \min x_i(k)} )
- 对于“望大特性”(MRR): ( x_i^*(k) = \frac{x_i(k) - \min x_i(k)}{\max x_i(k) - \min x_i(k)} )
- 得到预处理后的序列 ( X_i^* )。
-
计算灰色关联系数:
( \gamma(x_0^(k), x_i^(k)) = \frac{\min\limits_i \min\limits_k |x_0*(k)-x_i(k)| + \zeta \max\limits_i \max\limits_k |x_0*(k)-x_i(k)|}{|x_0*(k)-x_i(k)| + \zeta \max\limits_i \max\limits_k |x_0*(k)-x_i(k)|} )- 其中,( x_0^*(k) ) 是参考序列(通常取
[1, 1, 1],即理想最优值)。 - ( \zeta ) 是分辨系数,通常取0.5。
- 其中,( x_0^*(k) ) 是参考序列(通常取
-
计算灰色关联度(GRG):
( GRG_i = \frac{1}{n} \sum_{k=1}^n \gamma(x_0^(k), x_i^(k)) )- ( n ) 是响应指标的数量(本例中为3:Ra, MRR, Fc)。
- ( GRG_i ) 是一个介于0和1之间的值,越大代表该组参数的综合性越好。
至此,多目标问题转化为单目标问题:最大化灰色关联度(GRG)。
3.3 径向基函数神经网络 (RBFNN)
由于铣削过程是高度非线性的,需要一个强大的模型来拟合参数与GRG之间的复杂关系。RBFNN是一种三层前馈网络,具有收敛速度快、全局逼近能力强的优点。
- 输入层:3个节点,对应
[v_c, f_z, a_p]。 - 隐含层:使用高斯函数作为激活函数。节点数通过聚类算法(如K-means)或经验确定。
- 第j个节点的输出: ( \phi_j(X) = \exp(-\frac{||X - c_j||2}{2\sigma_j2}) )
- 其中,( c_j ) 是第j个基函数的中心,( \sigma_j ) 是宽度。
- 输出层:1个节点,输出预测的GRG值。
任务:用实验数据 [输入参数, 计算出的GRG] 来训练RBFNN,使其能够准确预测任意一组给定铣削参数的GRG。
3.4 粒子群优化算法 (PSO)
PSO模拟鸟群觅食行为,用于在RBFNN构建的复杂响应面上寻找全局最优解。
- 粒子:每个粒子代表一个候选的铣削参数组合
P_i = [v_c, f_z, a_p]。 - 搜索空间:每个参数的取值范围(由机床和刀具性能决定)。
- 适应度函数:训练好的RBFNN模型。将粒子的位置(一组参数)输入RBFNN,其输出的预测GRG值即为该粒子的适应度值。目标是最大化适应度。
- 更新公式:
- 速度更新: ( v_{id}(t+1) = w \cdot v_{id}(t) + c_1 r_1 (pbest_{id} - x_{id}(t)) + c_2 r_2 (gbest_{d} - x_{id}(t)) )
- 位置更新: ( x_{id}(t+1) = x_{id}(t) + v_{id}(t+1) )
- 流程:
- 初始化粒子群(随机位置和速度)。
- 评估每个粒子的适应度(通过RBFNN计算GRG)。
- 更新个体最优
pbest和全局最优gbest。 - 根据公式更新粒子的速度和位置。
- 重复步骤2-4,直到满足终止条件(如最大迭代次数或适应度收敛)。
PSO的最终输出 gbest 即为寻找到的最优铣削参数组合。
4. 实施步骤示例
-
实验设计与数据采集:
- 采用中心复合设计 或 Box-Behnken设计 等响应面方法,设计约20-30组实验。
- 在五轴加工中心上,使用特定刀具对N87试件进行铣削试验。
- 记录每组参数下的Ra(用轮廓仪)、MRR(计算得出)和Fc(用测力仪)。
-
GRA计算:
- 对采集到的Ra、MRR、Fc数据进行预处理。
- 计算每组实验的灰色关联系数和最终的GRG。
-
RBFNN建模:
- 将实验数据分为训练集(70-80%)和测试集(20-30%)。
- 使用训练集数据训练RBFNN,输入为
[v_c, f_z, a_p],输出为GRG。 - 使用测试集验证模型的预测精度(如计算R², RMSE)。
-
PSO优化:
- 设置PSO参数:种群大小(如30)、迭代次数(如100)、学习因子c1/c2、惯性权重w。
- 将训练好的RBFNN模型作为PSO的适应度函数。
- 运行PSO算法,寻找最大化GRG的最优参数组合
[v_c_opt, f_z_opt, a_p_opt]。
-
验证实验:
- 将PSO推荐的最优参数组合在实际机床上进行一次或多次验证实验。
- 测量实际的Ra、MRR、Fc,并计算实际的GRG。
- 比较实际GRG与预测GRG,验证整个优化系统的有效性和可靠性。























 833
833

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










