PINN预测圆形区域内的二维声场MATLAB实现

原创于 2025-11-24 22:23:32 发布 · 205 阅读

0 ·

CC 4.0 BY-SA版权

文章标签：

#matlab #PINN #二维声场

PINN物理信息神经网络专栏收录该内容

22 篇文章

订阅专栏

主要功能

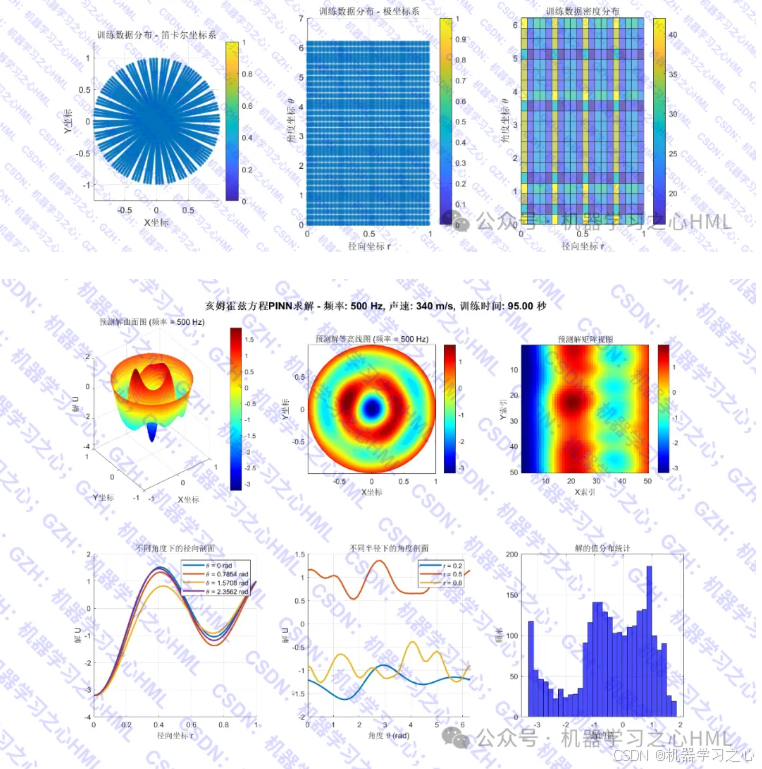
开发了一个基于物理信息神经网络(PINN)MATLAB代码，用于在圆形域上求解亥姆霍兹方程（预测圆形区域内的二维声场）。该代码通过深度学习技术将物理约束直接嵌入神经网络，无需传统数值方法的网格离散化。。

算法步骤

数据生成：使用Sobol序列在圆形域内生成准随机训练点
网络构建：构建深度全连接神经网络，使用sin激活函数
物理约束嵌入：通过自动微分计算PDE残差，构造试函数满足边界条件
优化训练：使用L-BFGS算法最小化物理约束损失函数
结果评估：在测试网格上评估解的质量并可视化

技术路线

物理信息神经网络(PINN)：将物理方程作为正则项加入损失函数
自动微分：精确计算偏微分方程所需的高阶导数
距离函数技巧：构造试函数自动满足边界条件
准随机采样：使用Sobol序列提高训练点分布均匀性
L-BFGS优化：内存高效的拟牛顿优化算法

公式原理

亥姆霍兹方程

$\nabla^{2} U + k^{2} U = 0, 其中 k = 2 π f / c$

试函数构造

$G = (1 - φ) U_{0} + φ U$
$φ = (R^{2} - (x^{2} + y^{2})) / (2 R)$
确保在边界上G=U₀（狄利克雷条件）

损失函数

$l oss = ∣∣ \nabla^{2} G + k^{2} G ∣ ∣_{2}^{2}$

网络架构

输入(x,y) → 全连接 → sin激活 → 全连接 → ... → 输出U

参数设定

物理参数

频率：freq = 500 Hz
声速：c = 340 m/s
圆域半径：R = 1
边界条件：U₀ = 1

网络参数

层数：numLayers = 5
神经元数：numNeurons = 90
激活函数：sin函数
初始化：He初始化（权重），零初始化（偏置）

优化参数

算法：L-BFGS
最大迭代：maxIterations = 100
最大函数评估：maxFuncEvaluations = 100
最优性容差：1e-5

运行环境

软件要求

MATLAB (推荐R2024b或更新版本)
必需工具箱：
- 深度学习工具箱 (Deep Learning Toolbox)
- 优化工具箱 (Optimization Toolbox)
- 统计和机器学习工具箱 (Statistics and Machine Learning Toolbox)

文件依赖

main.m → buildNet.m → initializeHe.m, initializeZeros.m
     ↓
modelLoss.m → model.m
     ↓
objectiveFunction.m → parameterVectorToStruct.m, parameterStructToVector.m