29、自然语言理解与生成问题中的深度学习：梯度下降与激活函数

最新推荐文章于 2025-11-24 19:11:26 发布
最新推荐文章于 2025-11-24 19:11:26 发布
阅读量12 收藏
点赞数
CC 4.0 BY-SA版权
分类专栏： 解锁NLP：从入门到精通 文章标签： 梯度下降 激活函数 深度学习
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.youkuaiyun.com/gitlab7runner/article/details/154384251

自然语言理解与生成问题中的深度学习：梯度下降与激活函数

1. 梯度下降计算

1.1 代码部分与梯度下降引入

首先我们来看代码部分，之后会进入核心的梯度下降计算环节。计算平方误差和的代码片段如下：
Code snippet for calculating sum of squared error

接下来我们进入梯度下降的计算。使用误差函数，我们能判断是否需要更新直线以得到最佳拟合直线，但如何更新直线正是本部分要探讨的内容。我们要思考如何最小化误差并得到最佳拟合直线。为了回答这个问题，我们先对梯度下降有个基本了解，在代码方面，我们只剩下最后一个函数 gradient_descent_runner() 了。参考下面这个用于理解梯度下降的 3D 图：
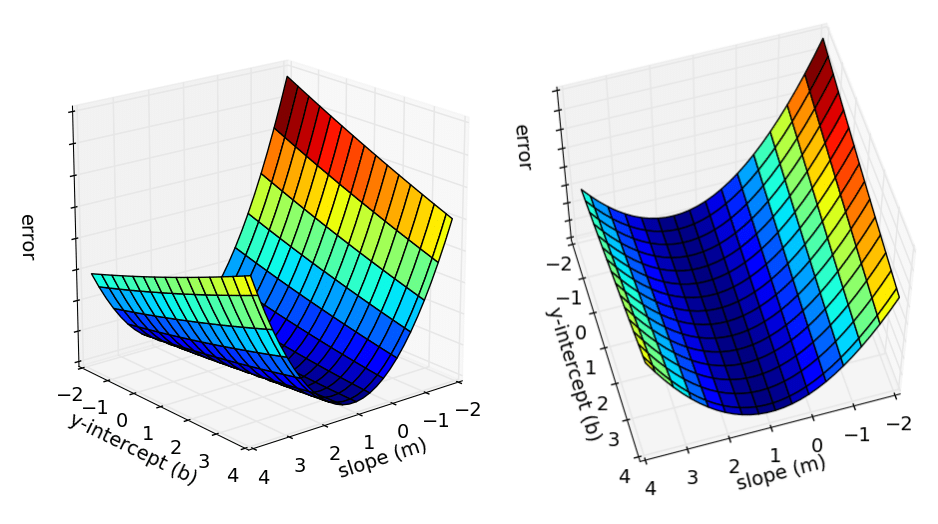
A 3D graph for understanding gradient descent

1.2 梯度下降的原理

这个 3D 图展示了斜率 m 、y 截距 b 和误差的所有可能值。x 轴是斜率值，y 轴是 y 截距，z 轴是误差值。我们的目标是找到误差最小的点。仔细观察图形会发现，曲线底部的误差值最小，这个误差最小的点在机器学习中被称为局部最小值。在复杂数据集中可能存在多个局部最小值，而这里我们的数据集简单，只有一个局部最

订阅专栏 解锁全文 会员秒杀 ¥9.9 重磅福利 超级会员免费看
现代C++中的从头开始深度学习：【4/8】梯度下降
gongdiwudu的专栏
08-08 7312
让我们通过在纯C++和特征中实现梯度下降来获得乐趣。跟随发表于10 分钟阅读9月日60一、说明中，我们将学习如何仅使用普通和现代C++编写必须知道的深度学习算法，例如卷积、反向传播、激活函数、优化器、深度神经网络等。在这个故事中，我们将通过引入算法来介绍数据中 2D 卷积核的拟合。我们将使用卷积和中引入的成本函数概念，将所有内容编码为现代C++和特征。这个故事是：C++的梯度下降...更多内容即将推出。二、函数逼近作为优化问题。
PyTorch深度学习实战（1）——神经网络与模型训练过程详解
盼小辉丶的博客
05-28 9万+
在本节中，我们将了解传统机器学习与人工神经网络间的差异，并了解如何在实现前向传播之前连接网络的各个层，以计算与网络当前权重对应的损失值；实现反向传播以优化权重达到最小化损失值的目标。并将实现网络的所有关键组成——前向传播、激活函数、损失函数、链式法则和梯度下降，从零开始构建并训练了一个简单的神经网络。
深度学习｜梯度下降法：误差最小化的权重参数
三余知行
09-09 2799
梯度下降法是神经网络训练的核心算法，通过梯度下降法，我们可以找到使损失函数最小的权重参数，从而使神经网络的推理结果更加准确。梯度下降法是一个迭代的过程，需要不断调整参数，直至损失函数收敛。在实际应用中，我们还会使用一些优化算法（如 `Adam`、`RMSprop` 等）来加速梯度下降的过程，具体的优化算法我们将在后续篇章中详细介绍。
一文掌握Sigmoid激活函数：深度学习的“隐形”英雄
码上飞扬的博客
07-08 3659
Sigmoid函数，有时也称作逻辑函数或Logistic函数，是深度学习和神经网络中最初期使用的一种激活函数。其中，e是自然对数的底数（约等于2.71828），x是神经元的输入。Sigmoid函数的图形是一个S形的曲线，也被称为S曲线（S-curve）。这个函数的核心特点是能够把输入值压缩到0到1的范围内。这种压缩的效果给予了它一些特别的优点，在机器学习和统计领域被广泛利用。Sigmoid函数曾是深度学习领域的宠儿，尽管现在它可能不再是第一选择，但在某些场景下它依旧显示出其不可替代的优势。
深度学习：激活函数
皮皮blog
05-04 3万+
激活函数神经网络神经元中，输入的 inputs 通过加权，求和后，还被作用了一个函数，这个函数就是激活函数 Activation Function。 为什么要用激活函数神经网络中激活函数的主要作用是提供网络的非线性建模能力，如不特别说明，激活函数一般而言是非线性函数。假设一个示例神经网络中仅包含线性卷积和全连接运算，那么该网络仅能够表达线性映射，即便增加网络的深度也依旧还是线性映射，难以有效建模
【深度学习】（三）神经网络中的学习：损失函数、梯度下降
一亿少女的梦
07-13 2060
“学习”指从训练数据中自动获取最优权重参数的过程。 数据处理 感知机收敛定理：通过有限次数的学习，线性可分问题是可解的。非线性问题不能通过自动学习来解决。 机器学习 深度学习 人为设计从图像转换为向量时使用的特征量；在用机器学习技术学习这些特征量的模式 不存在人为介入，全部都由机器来学习 对于不同的问题，必须使用适合的特征量 （端到端机器学习）与处理无关，从输入的原始数据中获得输出的目标结果。 特征量指可以从输入数据中准确地提取本质数据的转换器。 机器学习中，将数据分为训练数据/监督
【机器学习】深度探索：从基础概念到深度学习关键技术的全面解析——梯度下降、激活函数、正则化与批量归一化
Allen-
06-05 2728
随着科技的飞速发展，人工智能（AI）已经成为当今世界的热门话题。作为AI的核心技术之一，机器学习（Machine Learning, ML）在各个领域都发挥着举足轻重的作用。特别是在深度学习（Deep Learning, DL）领域中，机器学习提供了重要的理论支撑和实践指导。本文将通俗易懂地介绍机器学习的基本概念、原理和应用场景，并深入解析机器学习在深度学习领域中的重要作用。
深度学习知识点全面总结
热门推荐
专注大数据与人工智能技术分享，欢迎私信加群互相学习！
01-05 36万+
本文详细介绍深度学习概念及原理，参考网上相关资料汇总，内容包含众多章节，包括神经网络基础及常见深度学习网络结构介绍，用于个人学习总结，适合深度学习初学者学习。同时介绍机器学习常见的分类算法：SVM、神经网络、随机森林、逻辑回归、KNN、贝叶斯。常见的监督学习算法：感知机、SVM、人工神经网络、决策树、逻辑回归.........
TensorFlow深度学习实战（3）——深度学习中常用激活函数详解
盼小辉丶的博客
01-02 1万+
激活函数是神经网络中至关重要的一部分，它决定了神经元的输出以及神经网络模型的非线性特性。没有激活函数，神经网络就会变成一个简单的线性模型，无法处理复杂的任务。因此，激活函数的选择直接影响神经网络的表达能力和学习效果。
深度学习笔记（六）：激活函数常见问题总结
不积跬步，无以至千里！
07-20 4706
激活函数深入理解！
深度学习笔记：梯度与梯度衰减、滤波器
2301_81845359的博客
11-25 971
梯度、梯度爆炸、梯度消失、层次梯度衰减（HGD）、滤波器
反向传播、梯度下降与学习率：深度学习中的优化艺术
ciweic的博客
12-02 1451
反向传播、梯度下降和学习率是深度学习中不可或缺的三个概念。它们共同构成了深度学习模型训练的基石。理解这些概念及其相互作用对于设计和训练有效的深度学习模型至关重要。随着深度学习技术的不断发展，对这些基础概念的深入理解和创新应用将推动人工智能领域取得更多的突破。
鱼类识别系统【最新版】Python+TensorFlow+Vue3+Django+人工智能+深度学习+卷积神经网络算法
最新发布
2301_78372746的博客
11-24 660
鱼类识别系统，基于TensorFlow搭建卷积神经网络算法，通过收集了包括‘墨鱼’、‘多宝鱼’、‘带鱼’、‘石斑鱼’等在内的30种鱼类图像数据集进行训练，最后得到一个识别精度较高的模型，然后搭建Web可视化操作平台。前端后端：Django算法：TensorFlow、卷积神经网络算法具体功能系统分为管理员和用户两个角色，登录后根据角色显示其可访问的页面模块。登录系统后可发布、查看、编辑文章，创建文章功能中集成了markdown编辑器，可对文章进行编辑。
快速上手大模型：深度学习9（池化层、卷积神经网络1）
weixin_45728280的博客
11-20 1108
本文介绍了卷积神经网络的关键技术和经典模型。主要内容包括：1）池化层的作用与实现（最大/平均池化）；2）经典CNN模型（LeNet、AlexNet、VGG、NiN）的原理与代码实现，重点分析了AlexNet的架构改进（ReLU、Dropout、数据增强）和VGG的深层结构；3）计算机硬件配置查询方法（CPU、内存、GPU等），为模型训练提供硬件支持。文章提供了详细的PyTorch代码示例，涵盖网络构建、数据预处理和训练过程，并针对训练中的OOM问题给出了解决方案建议。
【Python TensorFlow】CNN-BiLSTM时序预测 卷积神经网络-双向长短期记忆神经网络组合模型（附代码）
vvoennvv的博客
11-19 499
本文提出了一种结合CNN与BiLSTM的混合神经网络模型（CNN-BiLSTM）用于多特征时序预测。该模型通过一维卷积提取局部时间特征，双向LSTM捕获长期依赖关系，实现了多步预测能力。算法流程包括数据预处理、网络构建（含卷积层、池化层、双向LSTM层）、模型训练（采用Adam优化器和MSE损失函数）及评估。实验采用电力负荷或风电场功率数据，通过滑动窗口构造样本并进行归一化处理，支持多输入多步预测。代码提供详细注释，可直接替换CSV/Excel数据集运行，包含完整的训练测试集划分和评估流程。
神经网络深度解析：从神经元到深度学习的进化之路
qq_51229257的博客
11-24 444
周志华《机器学习》第五章“神经网络”是连接传统机器学习与深度学习的桥梁——它从模拟人脑神经元的基本模型出发，逐步构建多层网络，核心突破是BP算法的提出，最终延伸到深度学习的核心思想。本章的核心逻辑是：通过“神经元加权求和+激活函数”构建基本单元，用多层结构拟合非线性关系，靠BP算法优化参数，再通过不同网络拓扑适应不同任务。本文将从“基础模型→核心算法→代码实现→习题解答”四个维度，用通俗比喻和实例拆解第五章的核心知识，帮你吃透神经网络的设计原理与工程实践。神经网络的最小单元是神经元，源于1943年提出的M-
李沐动手学深度学习笔记（2）---卷积神经网络
2301_80484013的博客
11-23 803
定义： 是 PyTorch 所有神经网络层、模型的基类（base class）。 所有的网络层（Linear、Conv2d、RNN等）以及你自己写的自定义网络，都必须继承它。特点：举例： Block（块，结构单元） 定义： Block 并不是 PyTorch 中的一个正式类名，而是我们在设计网络时人为定义的中间层次结构。 它是由若干 组成的一个子结构。用途：举例（ResNet 残差块）： Sequential（顺序容器） 定义： 是 的一种特殊子类，用来按顺序堆叠层，让代码更简洁。特点：
深度学习之基于paddle的多机训练资源配置
qq_42936727的博客
11-24 22
实际应用时，常会遇到更加复杂的机器学习或深度学习任务，需要运算速度更高的硬件（如GPU、NPU），甚至同时使用多个机器共同训练一个任务（多卡训练和多机训练）
人工智能、机器学习与深度学习：从概念到实践
已掌握java全栈，简单的java项目逻辑。目前正在学习鸿蒙开发，有兴趣的小伙伴可以一起学习！！！
11-21 985
今天开始去探索ai的路程，带领大家实现从0到1的探索之路！！！ 在当今科技浪潮中，“人工智能”（Artificial Intelligence, AI）已成为家喻户晓的热词。然而，很多人对“AI”“机器学习”（Machine Learning, ML）和“深度学习”（Deep Learning, DL）之间的关系感到困惑。它们究竟是同一事物的不同叫法，还是层层递进的技术体系？本文将用通俗语言厘清三者的关系，并通过经典案例帮助你建立清晰的认知框架。
评论
成就一亿技术人!
拼手气红包6.0元
还能输入1000个字符  | 博主筛选后可见
 
红包 添加红包
表情包 插入表情
表情包 代码片
 条评论被折叠 查看
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值