FastPlanner论文解读（二）——B样条轨迹优化

最新推荐文章于 2025-03-03 10:45:53 发布
原创 最新推荐文章于 2025-03-03 10:45:53 发布 · 2.9k 阅读 · 39 ·
CC 4.0 BY-SA版权
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
文章标签：

#无人机 #c++ #机器人

        在前端搜索出来的路径并不能保证其最优性，而是一个次优的路径（在实践中可以忍受对最优性的一些牺牲），同时，因为在前端路径搜索过程中，没有考虑与障碍物的距离信息，搜索出来的路径基本上是很靠近障碍物的。因此我们需要在后端去优化轨迹的平滑性和与障碍物的距离，这里采用B样条类的轨迹进行优化，主要利用其凸包性质。

一、B样条轨迹的介绍

1.贝塞尔曲线

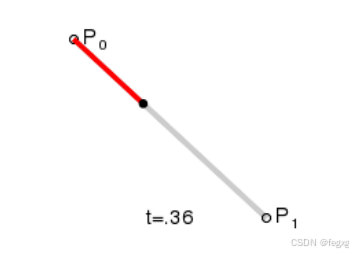
假设有两个点P0和P1，则过这两个点的曲线方程为：

B(t)=P_{0}+(1-t)P_{1}

t在0到1之间变化时，实际上该曲线B(t)表示过P0和P1的线段。

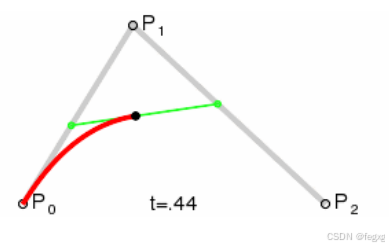
三个点P0、P1和P2时，构造其贝塞尔曲线：

首先构造P0P1线段：P_{0}P_{1}=P_{0}+(1-t)P_{1}

再构造P1P2线段：P_{1}P_{2}=P_{1}+(1-t)P_{2}

从P0P1上选一个点P0,1，P1P2上选一个点P1,2，由这两个点构成的曲线方程为：

P_{2}=P_{0,1}+(1-t)P_{1,2}

将P0,1和P1,2的方程带入进去后得到二阶的贝塞尔曲线方程为：

B(t)=(1-t)^{2}P_{0}+2(1-t)tP_{1}+t^{2}P_{2}

同理可以构造三阶的贝塞尔曲线：

B(t)=(1-t)^{3}P_{0}+3(1-t)^{2}tP_{1}+3(1-t)t^{2}P_{2}+t^{3}P_{3}

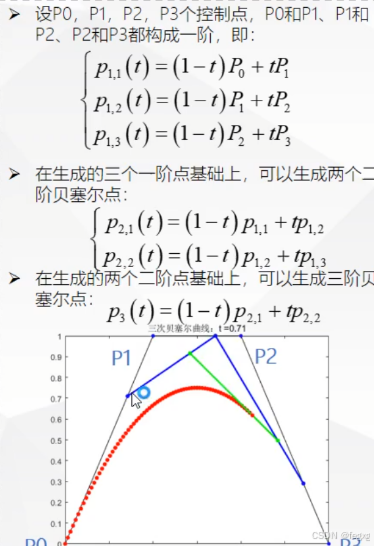
这里给出n阶贝塞尔曲线的表达式：

B(t)=\sum_{i=0}^{n}C_{n}^{i}(1-t)^{n-i}t^{i}P_{i}

贝塞尔曲线有以下的特点：

1.通过控制点{P1,P2...Pn}来控制曲线的形状

2.曲线通过起始点P1，终止点Pn，但不通过中间的控制点

3.贝塞尔曲线的阶次数等于控制点数量减一，3个点对应二阶曲线

4.曲线总是在控制点组成的凸包内部，若凸包之间不相交，则曲线也不相交

5.令基函数为：B_{n,i}=C_{n}^{i}(1-t)^{n-i}t^{i}，则其导数也为基函数：

B(t)^{1}_{i,n}=n(B_{i-1,n-1}(t)-B_{i,n-1}(t))

则说明贝塞尔曲线的导数也为贝塞尔曲线，这样对于速度V，加速度A，同样可以使用贝塞尔曲线的方式来表示来达到一些要求。(如范围限制可以转为控制点的限制)

贝塞尔曲线还有一些缺点：

1.多项式的阶数和控制点的个数相关，控制点数量过多后，多项式阶数太高

2.改变一个控制点将会改变整个曲线，难以局部进行修改

3.确保曲线连接处光滑的条件为连接点与其两侧的控制点共线，太复杂

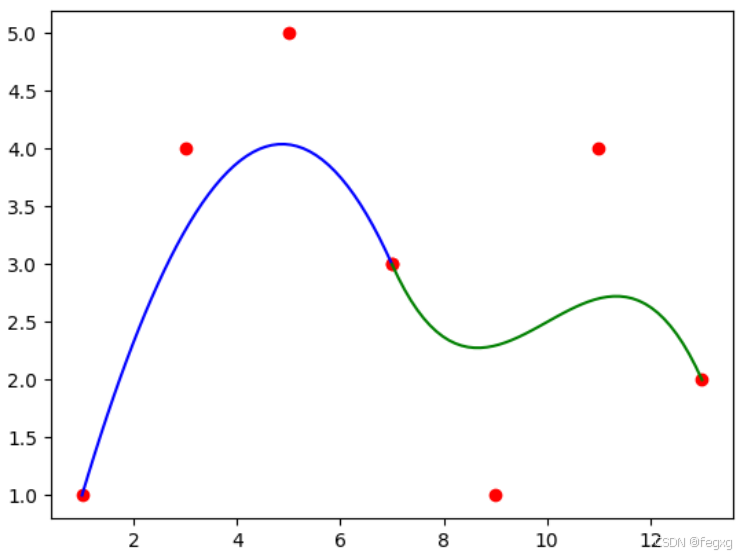
为了解决这些缺点提出了B样条曲线。

2.B样条曲线

1.定义

为了使控制点的改动影响更小，人为的将曲线分为若干段，使得各部分之间有影响但也有一定的独立性，改变控制点只影响局部。

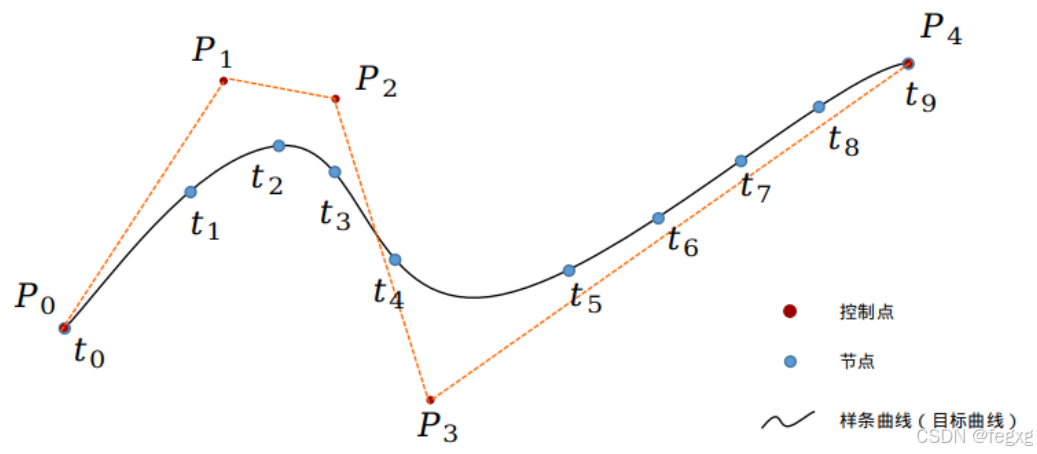
曲线段数为m（即节点向量为[t0,t1,...tm]），节点的个数为m+1，多项式的次数为pb（下图中的k即是pb），控制点个数为n+1，有如下关系式成立：

m=n+1+pb

2.B样条曲线计算

再看贝塞尔曲线的表达式，B(t)=\sum_{i=0}^{n}C_{n}^{i}(1-t)^{n-i}t^{i}P_{i}，其本质上是控制点前加上权重的累加和，即B(t)=\sum_{i=0}^{n}W_{i}P_{i}，Wi=B_{i,k}(t)，其中k代表最高次，如五个点的基函数为B_{0,4}、B_{1,4}、B_{2,4}、B_{3,4}、B_{4,4}，基函数的计算是通过如下表的来推算的：

第一列的值规定，当t落在[tj,tj+1]时，对应该区间的bi,0值为1，其余值为0，如：

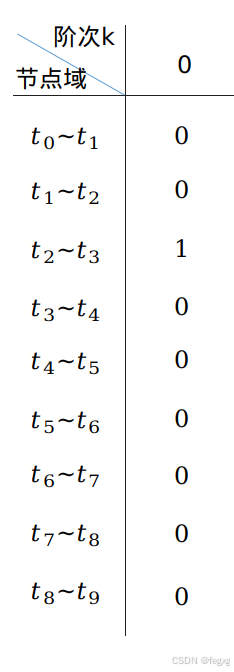
当k大于0时，以k=1为例子，

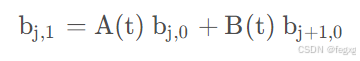
这里 A(t), B(t) 是关于 t 的一次幂函数。具体为

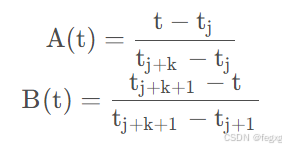
即bi,k是左边和左下两个值的加权和。

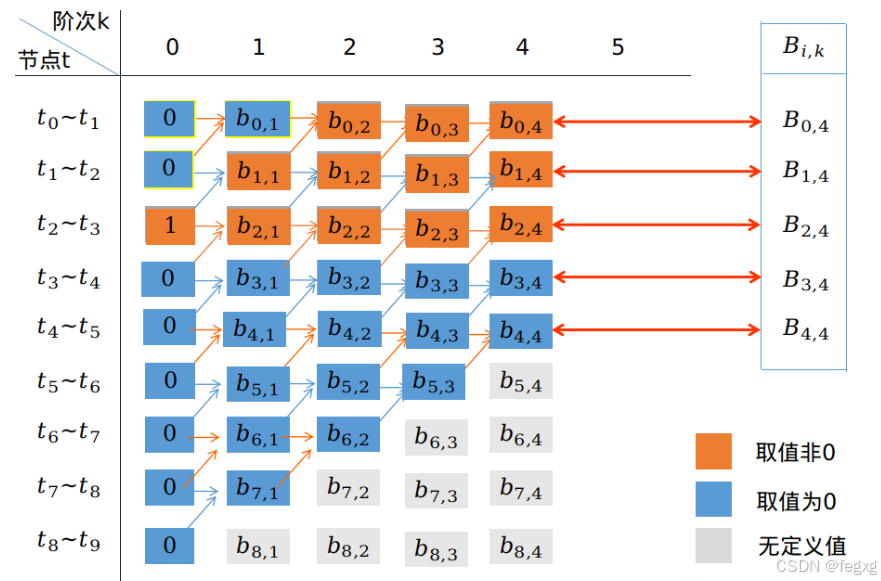
由图中可以看出，当t∈[tj,tj+1]时，非零的B_{j,k}值为：B_{j-k,k}到B_{j,k}，即[tj,tj+1]内的曲线，由第j-pb到j共pb+1个控制点决定，

即：

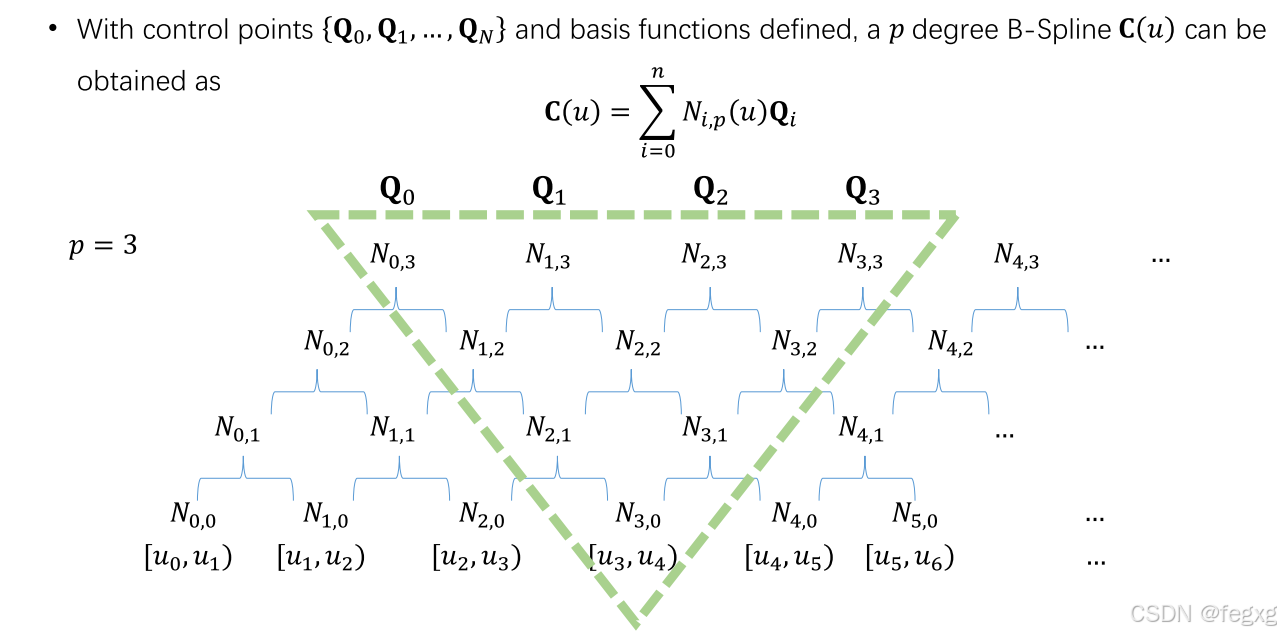
同样的，控制点Qi对应的影响区间为[ti,ti+pb+1]，如基函数W0，即控制点Q0的非零区域为t0-t4

即：

同样，我们可以看出，当t∈[t4,t5]时，Bi,4都是非零值，则说明该区间的点是由基函数完全定义（基函数和控制点的加权和，没有哪一项基函数为0）。一般性的，t的范围为[tpb,tm-pb]，而不是[t0,tm]。

均匀B样条曲线则是节点向量是均匀分布的，如：

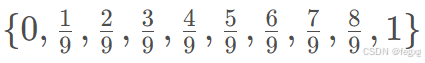
非均匀B样条的节点向量则不是均匀分布的

当我们值得t时，可以通过Dedoor公式进行递推计算系数（基函数Bi,k）：

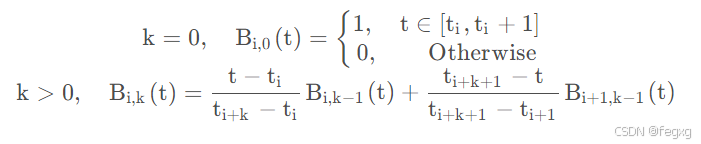
再根据B样条曲线公式B(t)=\sum_{i=0}^{n}B_{i,k}(t)P_{i}计算出t时刻对应在B样条曲线的位置坐标。

3.fastplanner中的B样条轨迹表达式

在fastplanner中，B样条曲线的公式如下：这里的m对应我们之前的j

这里

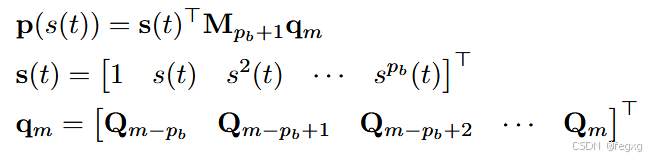
其中

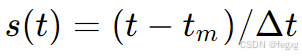
首先我们的次数为pb，则我们的B样条曲线是一段一段pb次的多项式拼接，这里t的区间为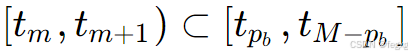

因此第一步，将时间t归一化到区间[tm,tm+1]上，得到s(t)。

由前面的内容可以知道，[tj,tj+1]时间段对应的控制点为Qm-pb到Qm，而控制点控制点Qj对应的影响区间为[tj,tj+pb+1]，则如图所示：

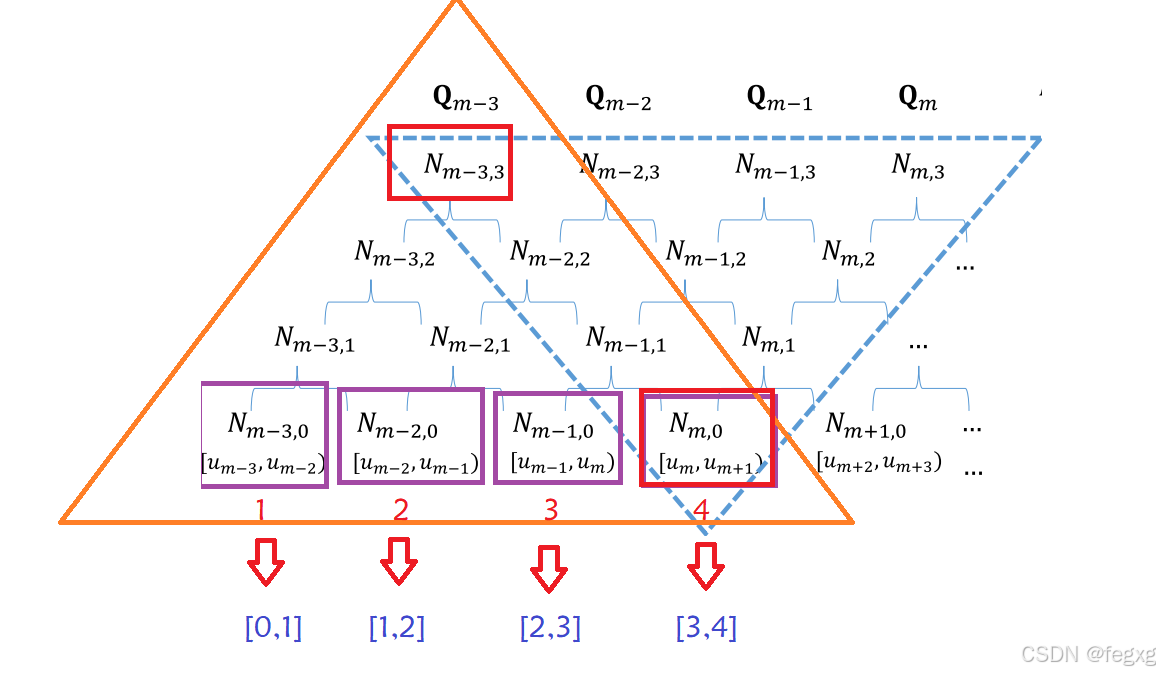
        通过前面的Dedoor递推公式，我们可以得到基函数Bi,k（这里图中就是Ni,k）在其不同时间区间的表达式，我们要计算的是[tm,tm+1]区间，因此我们把各个基函数在[tm,tm+1]的表达式写出来，这里要注意的是，我们之前做的归一化变化t是在[tm，tm+1]区间，而计算基函数的表达式时，基函数自身的非零区间为[tj,tj+pb+1]，比如图中Nm-3,3的非零区间为um-3到um+1，因此这里的s(t)=3+s(t)，3对应的是前面三个区间的长度（归一化）。

然后将表达式的系数项和s(t)的多项式分离，得到s(t)^{T}M_{pb+1}，最终得到表达式为

p(s(t))=s(t)^{T}M_{pb+1}q_{m}

在代码中是用NonUniformBspline类来表示B样条曲线：

#ifndef _UNIFORM_BSPLINE_H_
#define _UNIFORM_BSPLINE_H_

#include <Eigen/Eigen>
#include <algorithm>
#include <iostream>

using namespace std;

namespace ego_planner
{
  // An implementation of non-uniform B-spline with different dimensions
  // It also represents uniform B-spline which is a special case of non-uniform
  class UniformBspline
  {
  private:
    // control points for B-spline with different dimensions.
    // Each row represents one single control point
    // The dimension is determined by column number
    // e.g. B-spline with N points in 3D space -> Nx3 matrix
    Eigen::MatrixXd control_points_;//储存控制点

    int p_, n_, m_;     // p degree, n+1 control points, m = n+p+1，p_是多项式阶数，n_是控制点数量，m_节点数量
    Eigen::VectorXd u_; // knots vector，u_是节点向量，[0,1/4,1/2 ...]
    double interval_;   // knot span \delta t//时间间隔

    Eigen::MatrixXd getDerivativeControlPoints();

    double limit_vel_, limit_acc_, limit_ratio_, feasibility_tolerance_; // physical limits and time adjustment ratio，//物理限制，速度加速度调整比例和容忍度

  public:
    UniformBspline() {}
    UniformBspline(const Eigen::MatrixXd &points, const int &order, const double &interval);//构造函数
    ~UniformBspline();

    Eigen::MatrixXd get_control_points(void) { return control_points_; }//获取控制点矩阵

    // initialize as an uniform B-spline
    void setUniformBspline(const Eigen::MatrixXd &points, const int &order, const double &interval);//设置控制点、阶数和间隔，初始化一个均匀B样条

    // get / set basic bspline info

    void setKnot(const Eigen::VectorXd &knot);//设置节点向量
    Eigen::VectorXd getKnot();//获取节点向量
    Eigen::MatrixXd getControlPoint();//获取B样条的时间跨度
    double getInterval();//获取时间间隔
    bool getTimeSpan(double &um, double &um_p);//获取时间跨度

    // compute position / derivative

    Eigen::VectorXd evaluateDeBoor(const double &u);//给定u，评估在B样条曲线的什么位置                                             // use u \in [up, u_mp]
    inline Eigen::VectorXd evaluateDeBoorT(const double &t) { return evaluateDeBoor(t + u_(p_)); } // use t \in [0, duration]//给定时间t，判断在B样条什么位置
    UniformBspline getDerivative();//获取导数信息

    // 3D B-spline interpolation of points in point_set, with boundary vel&acc
    // constraints
    // input : (K+2) points with boundary vel/acc; ts
    // output: (K+6) control_pts
    static void parameterizeToBspline(const double &ts, const vector<Eigen::Vector3d> &point_set,
                                      const vector<Eigen::Vector3d> &start_end_derivative,
                                      Eigen::MatrixXd &ctrl_pts);//将给定的轨迹点变为控制点

    /* check feasibility, adjust time */

    void setPhysicalLimits(const double &vel, const double &acc, const double &tolerance);//设置物理限制
    bool checkFeasibility(double &ratio, bool show = false);//检查是否符合物理约束
    void lengthenTime(const double &ratio);//通过比例调整轨迹的时间长度

    /* for performance evaluation */

    double getTimeSum();//获取B样条的总时间
    double getLength(const double &res = 0.01);//获取B样条的总长度
    double getJerk();//获取轨迹的jerk
    void getMeanAndMaxVel(double &mean_v, double &max_v);//获取轨迹平均速度和最大速度
    void getMeanAndMaxAcc(double &mean_a, double &max_a);//获取轨迹的平均加速度和最大加速度

    EIGEN_MAKE_ALIGNED_OPERATOR_NEW
  };
} // namespace ego_planner
#endif

这里的成员变量主要为：

control_points_：存储 B-Spline 轨迹的控制点，每行对应一个 3D 控制点。
p_：B-Spline 的阶数。
n_：控制点的数量（n+1 个控制点）。
m_：节点向量的维度 m = n + p + 1。
u_：节点向量（Knots），用于参数化曲线。
interval_：轨迹的时间间隔 \delta t，影响轨迹的平滑程度。
limit_vel_：速度上限
limit_acc_：加速度上限
limit_ratio_：时间调整的比例

主要成员函数为：

setKnot(knot)	设置 B-Spline 的节点向量 u_。
getKnot()	获取节点向量 u_。
getControlPoint()	获取控制点矩阵 control_points_。
getInterval()	获取轨迹时间间隔 interval_。
getTimeSpan(um, um_p)	获取轨迹的时间范围 [u_min, u_max]。
getHeadTailPts()	获取轨迹的起点 & 终点的状态信息（位置、速度等）。
evaluateDeBoor(u)	计算 参数 u 处 的轨迹点（De Boor 算法）。
evaluateDeBoorT(t)	计算 时间 t 处 的轨迹点（时间映射到 u）。
getDerivative()	计算轨迹的导数（速度、加速度）。
parameterizeToBspline(ts, point_set, start_end_derivative, ctrl_pts)  通过轨迹点计算控制点 
setPhysicalLimits(vel, acc)	设置速度 & 加速度限制。
checkFeasibility(show)	检查轨迹是否可行（是否超出速度 & 加速度限制）。
checkRatio()	计算时间调整比例（若不满足约束，需要调整时间）。
lengthenTime(ratio)	按 ratio 扩展轨迹时间，降低加速度。
reallocateTime(show)	重新分配轨迹时间，确保满足动力学约束。
getTimeSum()	获取轨迹总时间。
getLength(res)	计算轨迹总长度（步长 res 控制精度）。
getJerk()	计算轨迹的jerk。
getMeanAndMaxVel(mean_v, max_v)	获取 平均 & 最大速度。
getMeanAndMaxAcc(mean_a, max_a)	获取 平均 & 最大加速度

4.B样条的特点

B样条有许多特点：

1.每个区间仅由相邻的几个控制点完全描述，即[tj,tj+1]时间段对应的控制点为Qm-pb到Qm

2.在多项式阶数大于等于1时，B样条是连续的曲线，随着控制点的增加，B样条曲线会在原曲线的基础上不断进行扩展，而不会改变整个轨迹

3.B样条的导数也是B样条

4.凸包性，轨迹始终会在包含了所有控制点的最小凸多边形中

以上的特点包括了贝塞尔曲线的特点，同时克服了贝塞尔曲线的一些缺点。

二、凸包特性的应用

B样条的凸包特性保证了B样条可以通过凸包来实现无碰撞性，如以下的图：

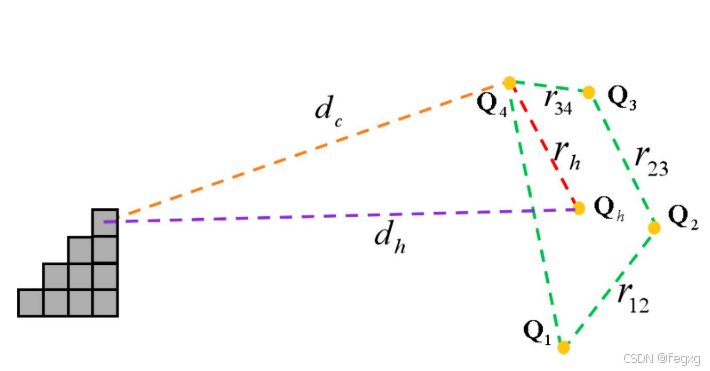
dh是控制点构成的凸包中任意一个点Qh到障碍物栅格区间中任意一个点的距离，dc是控制点到障碍物栅格区间该点的距离，Qh到凸包的控制点的距离为rh，r12，r23，r34是控制点之间的距离。根据三角形的特性，dh>dc-rh，而rh<r12+r23+r34，因此可以推导出dh>dc-(r12+r23+r34)，由此可以得到：

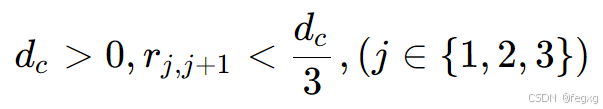
只要保证障碍物到凸包顶点的距离大于0，满足rj,j+1<dc/3，就能保证凸包一定在障碍物外面，则根据凸包特性，轨迹也一定在障碍物外面。

三、优化问题的构建

对于pb阶，N+1个控制点的B样条轨迹，控制点集合为{Q0,Q1,...QN}，我们只优化中间N+1-2pb个控制点，{Qpb,Qpb+1,...,QN-pb}，开头和结尾的各pb个控制点由起始和终端状态来决定。

代价函数为：

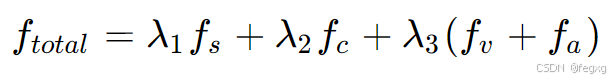
第一项fs代表轨迹平滑项，第二项fc代表碰撞项（安全性），第三项fv+fa是动力学可行项，λ1，λ2，λ3是权重（超参数）。

1.平滑项fs

Fast Planner中通过捕获轨迹的几何信息并且不依赖于时间分配的函数来定义平滑成本fs，不同于用jerk和snap的平方积分做平滑项，因为优化之后时间分配可能会发生改变。

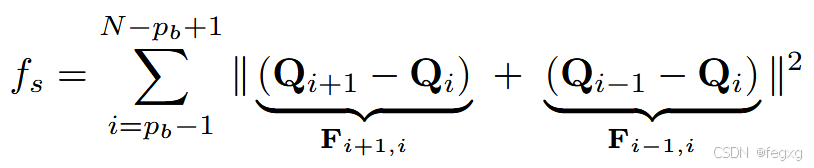
该公式实际是在Qi点两个方向的力（论文中叫做elastic band），如果所有项都等于零，则所有控制点将均匀分布在一条直线上，这是理想的平滑线。

平滑项的代价和导数计算代码如下：

void BsplineOptimizer::calcSmoothnessCost(const vector<Eigen::Vector3d> &q, double &cost,
                                            vector<Eigen::Vector3d> &gradient)
  {
    // q是控制点集合，cost是输出的平滑项cost，gradient是输出平滑项的梯度值，用于优化
    // 平滑项cost计算
    cost = 0.0;
    Eigen::Vector3d zero(0, 0, 0);
    std::fill(gradient.begin(), gradient.end(), zero);
    Eigen::Vector3d jerk, temp_j;

    for (int i = 0; i < q.size() - order_; i++)
    {
      /* evaluate jerk */
      jerk = q[i + 3] - 3 * q[i + 2] + 3 * q[i + 1] - q[i];
      cost += jerk.squaredNorm();
      temp_j = 2.0 * jerk;
      /* jerk gradient */
      gradient[i + 0] += -temp_j;       // qi点的梯度贡献值
      gradient[i + 1] += 3.0 * temp_j;  // 对qi+1点的梯度贡献值
      gradient[i + 2] += -3.0 * temp_j; // 对qi+2点的梯度贡献值
      gradient[i + 3] += temp_j;        // 对qi+3点的梯度贡献值
    }
  }

代码实现中使用的是jerk的平方项来计算smooth项，对应的控制点是Qi到Qi+3，其导数如代码中所示，这里使用了一个&gradient来记录整体计算cost过程中的每个控制点的Qi的梯度值。用&cost来记录总的cost值。

2.障碍项

Fast Planner中的碰撞成本被公式化为作用在每个控制点上的障碍物的排斥力，表达式为：

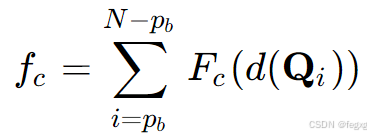
d(Qi)是Qi和最近的障碍物的距离，Fc函数是一个可微的势函数，表达式为：

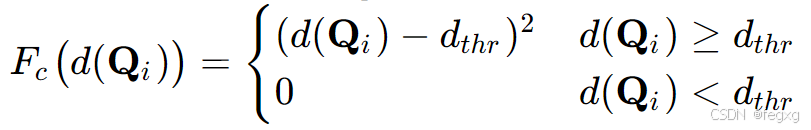
dthr是一个threhold，用于衡量和障碍物之间的距离。

当d(Qi)小于dthr时，不做惩罚，当d(Qi)超过了阈值，则做二次函数的惩罚。

之前由凸包性得出，rj,j+1<dc/3，这个条件，其实这个条件是否满足完全取决于我们在构造B样条的时候，如何进行参数化，如果控制点取的密一些，时间间隔短一些，这个条件就很容易满足了，一般取rj,j+1<0.2时，基本上都能满足。

障碍项的cost和导数计算代码如下所示：

void BsplineOptimizer::calcDistanceCost(const vector<Eigen::Vector3d> &q, double &cost,
                                          vector<Eigen::Vector3d> &gradient)
  {
    // q为控制点，cost是障碍项的cost，gradient是梯度
    // 障碍项cost计算
    cost = 0.0;
    Eigen::Vector3d zero(0, 0, 0);
    std::fill(gradient.begin(), gradient.end(), zero);

    double dist;
    Eigen::Vector3d dist_grad, g_zero(0, 0, 0);

    int end_idx = (cost_function_ & ENDPOINT) ? q.size() : q.size() - order_; // 根据条件判断是否计算终点的障碍代价，如果有ENDPOINT标志符则处理整个轨迹，否则忽略末尾的pb个点

    for (int i = order_; i < end_idx; i++)
    {
      edt_environment_->evaluateEDTWithGrad(q[i], -1.0, dist, dist_grad); // 计算控制点与障碍物的距离和梯度，即公式中的d(Qi)函数的值和梯度
      if (dist_grad.norm() > 1e-4)
        dist_grad.normalize(); // 对梯度做规范化

      if (dist < dist0_)
      {                                                   // 小于threshold做惩罚
        cost += pow(dist - dist0_, 2);                    // cost项(d(Qi)-dthr)^2
        gradient[i] += 2.0 * (dist - dist0_) * dist_grad; // 梯度项2(d(Qi)-dthr)*d_grad
      }
    }
  }

这里的dist0_是公式里的dthr，使用evaluateEDTWithGrad函数计算出d(Qi)的值，存放在dist里，梯度记录在dist_grad中，这个梯度是d()函数的导数在Qi的值。所以这里求导后得到梯度值为2(d(Qi)-dthr)*d_grad。

3.动力学可行项

动力学可行项是保证速度v和加速度a不超过限制，在xyz三个维度上，若加速度或速度的平方小于设定的最大值的平方时，该项代价值为0，大于设定的最大值的平方时为二次函数的惩罚。其表达式如下所示：

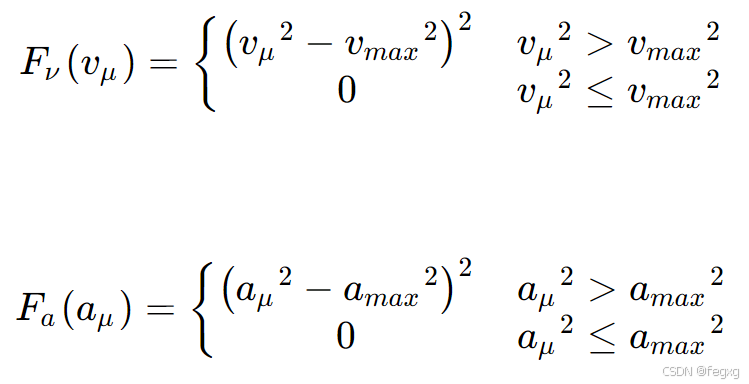
由于B样条曲线的导数也是B样条，所以利用凸包特性，只要保证V的控制点和A的控制点在范围之内，就能保证速度v和加速度a在范围内，对每个维度的控制点进行检查惩罚。内存是遍历每个点，外层是遍历每个维度。

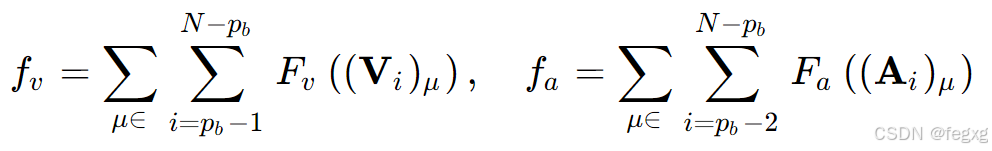
这里V和A的计算表达式为：

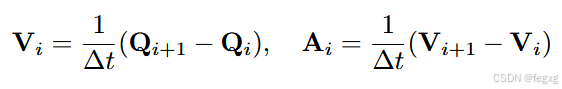
动力学可行项的cost和导数的计算为：

void BsplineOptimizer::calcFeasibilityCost(const vector<Eigen::Vector3d> &q, double &cost,
                                             vector<Eigen::Vector3d> &gradient)
  {
    // q是控制点，cost是动力学可行项的cost，gradient是梯度
    // 动力学可行性项cost计算
    cost = 0.0;
    Eigen::Vector3d zero(0, 0, 0);
    std::fill(gradient.begin(), gradient.end(), zero);

    /* abbreviation */
    double ts, vm2, am2, ts_inv2, ts_inv4;
    vm2 = max_vel_ * max_vel_;
    am2 = max_acc_ * max_acc_;

    ts = bspline_interval_;
    ts_inv2 = 1 / ts / ts;
    ts_inv4 = ts_inv2 * ts_inv2;

    /* velocity feasibility */
    for (int i = 0; i < q.size() - 1; i++)
    {
      Eigen::Vector3d vi = q[i + 1] - q[i];

      for (int j = 0; j < 3; j++)
      {
        double vd = vi(j) * vi(j) * ts_inv2 - vm2; // Vi^2-vmax^2,Vi=(Qi+1-Qi)/ts
        if (vd > 0.0)
        {
          cost += pow(vd, 2); // cost项

          double temp_v = 4.0 * vd * ts_inv2;
          gradient[i + 0](j) += -temp_v * vi(j);
          gradient[i + 1](j) += temp_v * vi(j); // 对上面的公式求导得到对控制点Qi和Qi+1的导数
        }
      }
    }

    /* acceleration feasibility */
    for (int i = 0; i < q.size() - 2; i++)
    {
      Eigen::Vector3d ai = q[i + 2] - 2 * q[i + 1] + q[i];

      for (int j = 0; j < 3; j++)
      {
        double ad = ai(j) * ai(j) * ts_inv4 - am2;
        if (ad > 0.0)
        {
          cost += pow(ad, 2);

          double temp_a = 4.0 * ad * ts_inv4;
          gradient[i + 0](j) += temp_a * ai(j); // 对控制点Qi、Qi+1和Qi+2的导数
          gradient[i + 1](j) += -2 * temp_a * ai(j);
          gradient[i + 2](j) += temp_a * ai(j);
        }
      }
    }
  }

这里用控制点来做动力学限制，速度Vi控制点的计算公式为：

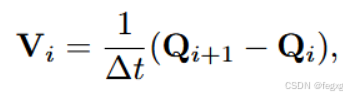
这里代码中用vi来记录q[i+1]-q[i]，ts_inv2来记录时间间隔的平方1/ts/ts，控制点Vi的平方就为：vi[j]*vi[j]*ts_inv2。

当速度Vi超限后，对其做平方项惩罚，再计算其对应控制点Qi的导数。加速度项同理，计算较为简单。

3.总的cost计算

最后使用combineCost函数对各个项的cost和导数汇总：

void BsplineOptimizer::combineCost(const std::vector<double> &x, std::vector<double> &grad,
                                     double &f_combine)
                                     //x代表当前的控制点集合，grad记录梯度信息，f_combine记录总的成本
    //用于计算多个成本项的加权和，计算每个控制点相关梯度
  {
    /* convert the NLopt format vector to control points. */

    // This solver can support 1D-3D B-spline optimization, but we use Vector3d to store each control point
    // For 1D case, the second and third elements are zero, and similar for the 2D case.
    for (int i = 0; i < order_; i++)//前pb个控制点
    {
      for (int j = 0; j < dim_; ++j)//每个维度
      {
        g_q_[i][j] = control_points_(i, j);//将控制点的格式转为二维数组的形式
      }
      for (int j = dim_; j < 3; ++j)//如果是低维度的控制点，将其剩余维度填充为0
      {
        g_q_[i][j] = 0.0;
      }
    }

    for (int i = 0; i < variable_num_ / dim_; i++)//x是个一维向量，控制点的维度为3，所以总个数为variable_num/3个，x里的控制点是需要优化的控制点，对应Qpb到QN-pb，前pb个和后pb个由初始点和目标点决定
    {
      for (int j = 0; j < dim_; ++j)
      {
        g_q_[i + order_][j] = x[dim_ * i + j];//用x来赋值剩下的控制点
      }
      for (int j = dim_; j < 3; ++j)
      {
        g_q_[i + order_][j] = 0.0;
      }
    }

    if (!(cost_function_ & ENDPOINT))//没有设置终点约束时，要处理最后的pb个控制点
    {
      for (int i = 0; i < order_; i++)
      {

        for (int j = 0; j < dim_; ++j)
        {
          g_q_[order_ + variable_num_ / dim_ + i][j] =
              control_points_(control_points_.rows() - order_ + i, j);
        }
        for (int j = dim_; j < 3; ++j)
        {
          g_q_[order_ + variable_num_ / dim_ + i][j] = 0.0;
        }
      }
    }

    f_combine = 0.0;
    grad.resize(variable_num_);
    fill(grad.begin(), grad.end(), 0.0);

    /*  evaluate costs and their gradient  */
    double f_smoothness, f_distance, f_feasibility, f_endpoint, f_guide, f_waypoints;
    f_smoothness = f_distance = f_feasibility = f_endpoint = f_guide = f_waypoints = 0.0;

    if (cost_function_ & SMOOTHNESS)
    {
      calcSmoothnessCost(g_q_, f_smoothness, g_smoothness_);//平滑项代价和梯度
      f_combine += lambda1_ * f_smoothness;//平滑项的代价由平滑项的cost乘以权重
      for (int i = 0; i < variable_num_ / dim_; i++)
        for (int j = 0; j < dim_; j++)
          grad[dim_ * i + j] += lambda1_ * g_smoothness_[i + order_](j);//梯度是一个一维向量，需要进行坐标的转化
    }
    if (cost_function_ & DISTANCE)
    {
      calcDistanceCost(g_q_, f_distance, g_distance_);//障碍项代价和梯度
      f_combine += lambda2_ * f_distance;
      for (int i = 0; i < variable_num_ / dim_; i++)
        for (int j = 0; j < dim_; j++)
          grad[dim_ * i + j] += lambda2_ * g_distance_[i + order_](j);
    }
    if (cost_function_ & FEASIBILITY)//动力学可行性项代价和梯度
    {
      calcFeasibilityCost(g_q_, f_feasibility, g_feasibility_);
      f_combine += lambda3_ * f_feasibility;
      for (int i = 0; i < variable_num_ / dim_; i++)
        for (int j = 0; j < dim_; j++)
          grad[dim_ * i + j] += lambda3_ * g_feasibility_[i + order_](j);
    }
    if (cost_function_ & ENDPOINT)
    {
      calcEndpointCost(g_q_, f_endpoint, g_endpoint_);
      f_combine += lambda4_ * f_endpoint;
      for (int i = 0; i < variable_num_ / dim_; i++)
        for (int j = 0; j < dim_; j++)
          grad[dim_ * i + j] += lambda4_ * g_endpoint_[i + order_](j);
    }
    if (cost_function_ & GUIDE)
    {
      calcGuideCost(g_q_, f_guide, g_guide_);
      f_combine += lambda5_ * f_guide;
      for (int i = 0; i < variable_num_ / dim_; i++)
        for (int j = 0; j < dim_; j++)
          grad[dim_ * i + j] += lambda5_ * g_guide_[i + order_](j);
    }
    if (cost_function_ & WAYPOINTS)
    {
      calcWaypointsCost(g_q_, f_waypoints, g_waypoints_);
      f_combine += lambda7_ * f_waypoints;
      for (int i = 0; i < variable_num_ / dim_; i++)
        for (int j = 0; j < dim_; j++)
          grad[dim_ * i + j] += lambda7_ * g_waypoints_[i + order_](j);
    }
    /*  print cost  */
    // if ((cost_function_ & WAYPOINTS) && iter_num_ % 10 == 0) {
    //   cout << iter_num_ << ", total: " << f_combine << ", acc: " << lambda8_ * f_view
    //        << ", waypt: " << lambda7_ * f_waypoints << endl;
    // }

    // if (optimization_phase_ == SECOND_PHASE) {
    //  << ", smooth: " << lambda1_ * f_smoothness
    //  << " , dist:" << lambda2_ * f_distance
    //  << ", fea: " << lambda3_ * f_feasibility << endl;
    // << ", end: " << lambda4_ * f_endpoint
    // << ", guide: " << lambda5_ * f_guide
    // }
  }

首先就是对前pb个点进行赋值：

for (int i = 0; i < order_; i++)//前pb个控制点
    {
      for (int j = 0; j < dim_; ++j)//每个维度
      {
        g_q_[i][j] = control_points_(i, j);//将控制点的格式转为二维数组的形式
      }
      for (int j = dim_; j < 3; ++j)//如果是低维度的控制点，将其剩余维度填充为0
      {
        g_q_[i][j] = 0.0;
      }
    }

将control_points_转为二维数组g_q_[][]，同时如果不是做xyz三维的优化，将其他多余的维度填为0。

中间的Qpb到QN-pb个点，用x向量来赋值，

for (int i = 0; i < variable_num_ / dim_; i++)//x是个一维向量，控制点的维度为3，所以总个数为variable_num/3个，x里的控制点是需要优化的控制点，对应Qpb到QN-pb，前pb个和后pb个由初始点和目标点决定
    {
      for (int j = 0; j < dim_; ++j)
      {
        g_q_[i + order_][j] = x[dim_ * i + j];//用x来赋值剩下的控制点
      }
      for (int j = dim_; j < 3; ++j)
      {
        g_q_[i + order_][j] = 0.0;
      }
    }

这里x是一维向量，即是将三维的控制点坐标拉成一维的，第i个点第j维的计算公式就是dim_*i+j，dim_就是控制点的维度，这里为3维。其余多余的维度用0来赋值。

这里control_points_是Bspline的总的N+1个控制点，而x传入的是points是我们中间需要优化的控制点变量。

然后对终点的pb个控制点处理

if (!(cost_function_ & ENDPOINT))//没有设置终点约束时，要处理最后的pb个控制点
    {
      for (int i = 0; i < order_; i++)
      {

        for (int j = 0; j < dim_; ++j)
        {
          g_q_[order_ + variable_num_ / dim_ + i][j] =
              control_points_(control_points_.rows() - order_ + i, j);
        }
        for (int j = dim_; j < 3; ++j)
        {
          g_q_[order_ + variable_num_ / dim_ + i][j] = 0.0;
        }
      }
    }

这里是用标志位来判断是否需要处理终点的pb个控制点，处理的点的范围即是control_points_(control_points_.rows() - order_ + i, j)，即QN-pb到QN。

赋值到二维数组g_q_，i+order_就是从第pb位置开始，再加上variable_num_/dim_（需要优化的控制点数量，这里对应中间的点），因此这里下标对应的是最后的pb个点。

之后便进行cost和导数的计算：

f_combine = 0.0;
grad.resize(variable_num_);
fill(grad.begin(), grad.end(), 0.0);

/*  evaluate costs and their gradient  */
double f_smoothness, f_distance, f_feasibility, f_endpoint, f_guide, f_waypoints;
f_smoothness = f_distance = f_feasibility = f_endpoint = f_guide = f_waypoints = 0.0;

首先初始化变量f_cost记录总的代价，grad记录梯度，且大小为variable_num_个，初始赋值为0。再定义各项的代价。

然后是各项代价和导数的计算，这里只说明平滑项、碰撞项和动力学可行项

if (cost_function_ & SMOOTHNESS)
    {
      calcSmoothnessCost(g_q_, f_smoothness, g_smoothness_);//平滑项代价和梯度
      f_combine += lambda1_ * f_smoothness;//平滑项的代价由平滑项的cost乘以权重
      for (int i = 0; i < variable_num_ / dim_; i++)
        for (int j = 0; j < dim_; j++)
          grad[dim_ * i + j] += lambda1_ * g_smoothness_[i + order_](j);//梯度是一个一维向量，需要进行坐标的转化
    }
    if (cost_function_ & DISTANCE)
    {
      calcDistanceCost(g_q_, f_distance, g_distance_);//障碍项代价和梯度
      f_combine += lambda2_ * f_distance;
      for (int i = 0; i < variable_num_ / dim_; i++)
        for (int j = 0; j < dim_; j++)
          grad[dim_ * i + j] += lambda2_ * g_distance_[i + order_](j);
    }
    if (cost_function_ & FEASIBILITY)//动力学可行性项代价和梯度
    {
      calcFeasibilityCost(g_q_, f_feasibility, g_feasibility_);
      f_combine += lambda3_ * f_feasibility;
      for (int i = 0; i < variable_num_ / dim_; i++)
        for (int j = 0; j < dim_; j++)
          grad[dim_ * i + j] += lambda3_ * g_feasibility_[i + order_](j);
    }

这里主要做了一个从各个项二维的梯度量转为grad中一维的梯度量的换算。

在函数optimize中，使用nlopt优化器求解该无约束优化问题。

nlopt::opt opt(nlopt::algorithm(isQuadratic() ? algorithm1_ : algorithm2_), variable_num_);

四、从前端轨迹点到B样条控制点

从前端采样得到的轨迹点到我们要优化的控制点中间还有个转化的过程，这个过程在fastplanner的代码中体现。

核心函数为：parameterizeToBspline

void NonUniformBspline::parameterizeToBspline(const double &ts, const vector<Eigen::Vector3d> &point_set,
                                                const vector<Eigen::Vector3d> &start_end_derivative,
                                                Eigen::MatrixXd &ctrl_pts)
  {
    // ts为时间间隔，point_set为前端搜索的路径点，start_end_derivative起点和终点的导数，ctrl_pts是生成的控制点,大小为(K+2)*3，K是轨迹点的数量
    if (ts <= 0)
    {
      cout << "[B-spline]:time step error." << endl;
      return;
    }

    if (point_set.size() < 2)
    {
      cout << "[B-spline]:point set have only " << point_set.size() << " points." << endl;
      return;
    }

    if (start_end_derivative.size() != 4)
    {
      cout << "[B-spline]:derivatives error." << endl;
    } // 进行检查，时间间隔必须大于0，轨迹点的数量必须大于2，起始和目标点的导数量数必须等于4

    int K = point_set.size(); // 轨迹点的数量

    // write A
    Eigen::Vector3d prow(3), vrow(3), arow(3);
    prow << 1, 4, 1;
    vrow << -1, 0, 1;
    arow << 1, -2, 1;

    Eigen::MatrixXd A = Eigen::MatrixXd::Zero(K + 4, K + 2); // A是参数化过程中的线性系统矩阵，大小为K+4*K+2

    for (int i = 0; i < K; ++i)
      A.block(i, i, 1, 3) = (1 / 6.0) * prow.transpose();

    A.block(K, 0, 1, 3) = (1 / 2.0 / ts) * vrow.transpose(); // block块，起点为前两个数，块的大小为后两个数
    A.block(K + 1, K - 1, 1, 3) = (1 / 2.0 / ts) * vrow.transpose();

    A.block(K + 2, 0, 1, 3) = (1 / ts / ts) * arow.transpose();
    A.block(K + 3, K - 1, 1, 3) = (1 / ts / ts) * arow.transpose();
    // cout << "A:\n" << A << endl;

    // A.block(0, 0, K, K + 2) = (1 / 6.0) * A.block(0, 0, K, K + 2);
    // A.block(K, 0, 2, K + 2) = (1 / 2.0 / ts) * A.block(K, 0, 2, K + 2);
    // A.row(K + 4) = (1 / ts / ts) * A.row(K + 4);
    // A.row(K + 5) = (1 / ts / ts) * A.row(K + 5);

    // write b
    Eigen::VectorXd bx(K + 4), by(K + 4), bz(K + 4);
    for (int i = 0; i < K; ++i)
    {
      bx(i) = point_set[i](0);
      by(i) = point_set[i](1);
      bz(i) = point_set[i](2);
    }

    for (int i = 0; i < 4; ++i)
    {
      bx(K + i) = start_end_derivative[i](0);
      by(K + i) = start_end_derivative[i](1);
      bz(K + i) = start_end_derivative[i](2);
    }

    // solve Ax = b
    Eigen::VectorXd px = A.colPivHouseholderQr().solve(bx); // 使用 QR 分解求解线性系统
    Eigen::VectorXd py = A.colPivHouseholderQr().solve(by);
    Eigen::VectorXd pz = A.colPivHouseholderQr().solve(bz);

    // convert to control pts
    ctrl_pts.resize(K + 2, 3);
    ctrl_pts.col(0) = px;
    ctrl_pts.col(1) = py;
    ctrl_pts.col(2) = pz; // 控制点三列分别为px，py，px，一共K+2个控制点

    // cout << "[B-spline]: parameterization ok." << endl;
  }

这里的核心思想是构造线性等式：

Aq_{m}=b

通过轨迹点构造矩阵A和b，从而求出控制点向量pm。

这里定义K代表轨迹点的数量（前端轨迹采样获得）。矩阵A的大小为K+4*K+2，控制点向量pm的大小为K+2*3，b向量的大小为K+4*3。

现在来构造A矩阵：

前K行，对应的是每个轨迹点的位置约束（一共K个轨迹点，共K个约束）。这里的计算公式为：

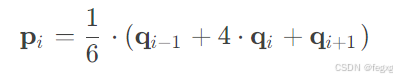
这里的权重是用基函数计算出来的。

因此，0-K-1行的A：A[k][K-1:K+1]=1/6[1,4,1]，k代表行，范围是0-K-1。

后面四行对应起始点和目标点的速度和加速度。

K行和K+1行对应的是起始点和目标点的速度约束：

V_{0}=\frac{1}{2\Delta t}(-P_{0}+P_{2})

V_{k}=\frac{1}{2\Delta t}(-P_{k-1}+P_{k+1})

对应A矩阵为：

A[K][0:2]=1/2Δt[-1,0,1],

A[K+1][k-1:k+1]=1/2Δt[-1,0,1],

K行和K+1行对应的是起始点和目标点的加速度约束：

A_{0}=\frac{1}{\Delta t^{2}}(P_{0}-2P_{1}+P_{2})

A_{K}=\frac{1}{\Delta t^{2}}(P_{K-1}-2P_{K}+P_{K+1})

对应A矩阵为：

A[K+2][0:2]=1/Δt^2[1,-2,1],

A[K+3][k-1:k+1]=1/2Δt^2[1,-2,1],

b向量前K行为位置px，py，pz，后四行为起终点的速度和加速度。

fegxg
关注
Fast Planner规划算法（二）—— Fast Planner后端之贝塞尔曲线与B样条曲线
慕羽★的博客
08-08 3687
本系列文章用于学习记录Fast-Planner规划算法的相关内容，主要学习资料是深蓝学院的移动机器人运动规划课程Fast Planner后端的主要任务是基于前端生成的轨迹，生成一条满足其他约束的轨迹，Fast Planner后端包含轨迹优化和迭代时间调整两部分
Fast Planner规划算法（三）—— Fast Planner后端之轨迹优化与轨迹优化与时间重分配
慕羽★的博客
08-08 3251
本系列文章用于学习记录Fast-Planner规划算法的相关内容，主要学习资料是深蓝学院的移动机器人运动规划课程
将FastPlanner后端基于B样条的轨迹优化封装单独可用的C++文件，并将三维轨迹将为2维轨迹，适用于地面小车实时规划
最新发布
10-31
将FastPlanner后端基于B样条的轨迹优化封装单独可用的C++文件，并将三维轨迹将为2维轨迹，适用于地面小车实时规划
FastPlanner论文解读（三）——后端时间优化及代码流程
fegxg的博客
02-06 1660
详细解读fastplanner论文和代码
【无人机路径规划】三维A星算法+B样条曲线优化无人机(UAV)路径规划
matlab_dingdang的博客
03-03 2220
无人机(UAV)技术近年来发展迅猛，在物流、巡检、遥感、救援等领域展现出巨大的应用潜力。其中，路径规划作为无人机自主飞行的核心技术之一，旨在寻找一条从起点到终点，同时满足各种约束条件的最优或次优飞行路径。在复杂的三维环境中，无人机需要考虑障碍物规避、飞行效率、能源消耗等多重因素，因此高效、可靠的路径规划算法至关重要。本文将深入探讨基于三维A*算法与B样条曲线优化的无人机路径规划方法，分析其原理、优势与挑战，并展望未来的发展方向。一、三维A*算法：基础与挑战A。
基于遗传算法B样条曲线优化在机器人轨迹规划中应用.
01-05
自适应遗传算法交叉变异算子的改进论文
Fast Planner——代码解读参考资料整理
怕什么真理无穷,进一寸有一寸的欢喜
02-13 8466
Fast planner代码解读参考资料整理
Fast-Planner论文阅读
qq_45858842的博客
06-27 1661
无人机路径规划有两个待解决的问题，一是在给定时间和有限机载电脑资源条件下难以保证高成功率的生成安全且符合动力学可行轨迹，在未知环境中高速飞行的无人机，应该在很短的时间内不断地重新生成轨迹，以避免出现紧急威胁。二是为了确保生成运动的动态可行性，速度和加速度的约束通常保守的执行，因此需要提高生成轨迹的攻击性以满足高飞行速度的应用。Fast采用基于启发式搜索和线性二次型最小时间控制的动态路径搜索方法。它在离散控制空间中有效地搜索一条安全、可行、时间最短的初始路径。
B样条曲线优化各种路径规划算法，matlab栅格地图。
m0_71097207的博客
05-18 1997
B样条曲线优化各种路径规划算法，matlab栅格地图。 ID:6998670946345345
Fast-Planner论文第一篇：Robust and Efficient Quadrotor Trajectory Generation for Fast Autonomous Flight
hongchennihao的博客
05-29 1552
摘要： 采用运动动力学路径搜索方法在离散化控制空间中寻找安全、运动可行、最短时间的初始轨迹。利用b样条的凸包特性，结合欧几里得距离场(EDF)的梯度信息和动态约束，采用b样条优化方法提高轨迹的平滑度和间隙。最后，通过将最终轨迹表示为非均匀b样条，采用迭代时间调整方法保证轨迹的动态可行和开放性。 引言 在四旋翼运动规划领域存在两个重要的未被解决的问题：1、有限的时间和板载计算资源下，现有工作不能保证高成功率地生成安全和运动动力学可行的轨迹；2、为保证运动动力学可行性，对速度和加速度进行了较大限制。 在本文中，
无人机多项式插值轨迹优化和B样条插值轨迹优化对比
03-21
本程序自己学习用！
用B样条函数对S形弯曲波导进行结构优化
02-13
S形弯曲波导是集成光器件中不可缺少的部分。在光开关阵列、星形耦合器以及阵列波导光栅等器件中,以及将多个元件集成到一个芯片上时,都需要很多的S形弯曲波导来实现波导的侧向位移和连接。其尺寸和损耗直接影响整个器件的损耗以及集成密度。弯曲波导插入损耗(不包括由于结构缺陷而产生的光的散射损耗)由两部分组成
A*算法C#实现，三次B样条优化
04-12
用于路径规划算法，A*源代码，三次B样条源代码 用于路径规划算法，A*源代码，三次B样条源代码 用于路径规划算法，A*源代码，三次B样条源代码
将EgoPlanner后端（纯净版）基于B样条的轨迹优化封装单独可用的C++文件，并将三维轨迹将为2维轨迹，适用于地面移动机器人实时局部路径规划
10-27
在此情境下，B样条曲线被用于轨迹优化，即通过调整曲线参数，使得在规划路径时能够生成符合特定性能指标的轨迹。 轨迹优化是路径规划中的一个核心环节，尤其是对于机器人来说，它需要处理和适应动态变化的环境，并...
Fast-Planner(三)详解后端B-Spline曲线优化
weixin_45534376的博客
03-25 3054
本文上接Fast-Planner的B-spline曲线生成详解，介绍B-spline曲线优化。如有问题，欢迎各位大佬评论指出，带着我一起进步。
【论文学习】fast-planner学习
weixin_45058446的博客
09-08 1617
fast planner学习
基于遗传算法优化B样条曲线
GYY8023的博客
05-30 1737
基于遗传算法优化B样条曲线一、B样条曲线学习二、遗传算法学习 一、B样条曲线学习 B-样条曲线入门 B-spline Curves 定义 二、遗传算法学习 详解遗传算法（含MATLAB代码）
先从路径优化开始学习FastPlanner之B样条曲线平滑路径（一）：从拉格朗日插值到B样条曲线
qq_51013517的博客
08-25 2303
B样条学习整理，易错点和关键点。我会列出学习他人的博客，但我不涉及具体推导，原理讲解，旨在于理解必须概念后写代码出效果和使用。
MATLAB B样条轨迹规划与多目标优化
gitblog_09751的博客
10-12 884
MATLAB B样条轨迹规划与多目标优化 【下载地址】MATLABB样条轨迹规划与多目标优化 本资源提供了一个基于MATLAB的B样条轨迹规划工具，结合多目标优化技术，实现了7次非均匀B样条轨迹规划。该工具采用了NSGA-II遗传算法，旨在优化轨迹的时间、能量和冲击，从而实现最优的轨迹规划效果 ...
fastplanner论文
03-17
- 后端精细化轨迹优化利用 SOCP 技术完成平滑处理。 ```python import numpy as np def esdf_update(grid_map, obstacle_points): """ 更新欧几里得带符号距离场 """ updated_esdf = grid_map.copy() for ...
评论
成就一亿技术人!
拼手气红包6.0元
还能输入1000个字符
 
红包 添加红包
表情包 插入表情
表情包 代码片
 条评论被折叠 查看
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值