FastPlanner论文解读（一）——前端路径搜索

本系列将更新FastPlanner论文内容对应代码的解读，其github的工程位置如下：

GitCode - 全球开发者的开源社区,开源代码托管平台

一、摘要

        在本文中，提出了一种稳健高效的四旋翼运动规划系统，主要架构如下：

1.kinodynamic 路径搜索方法在离散控制空间中找到一个安全的、kinodynamic 可行且时间最短初始轨迹。

2.我们通过 B 样条优化来改善轨迹的平滑度和间隙，该优化结合了来自欧几里得距离场 （EDF） 的梯度信息和动态约束，有效地利用了 B 样条的凸包特性。

3.将最终轨迹表示为非均匀 B 样条，采用迭代时间调整方法来保证动态可行和非保守轨迹。

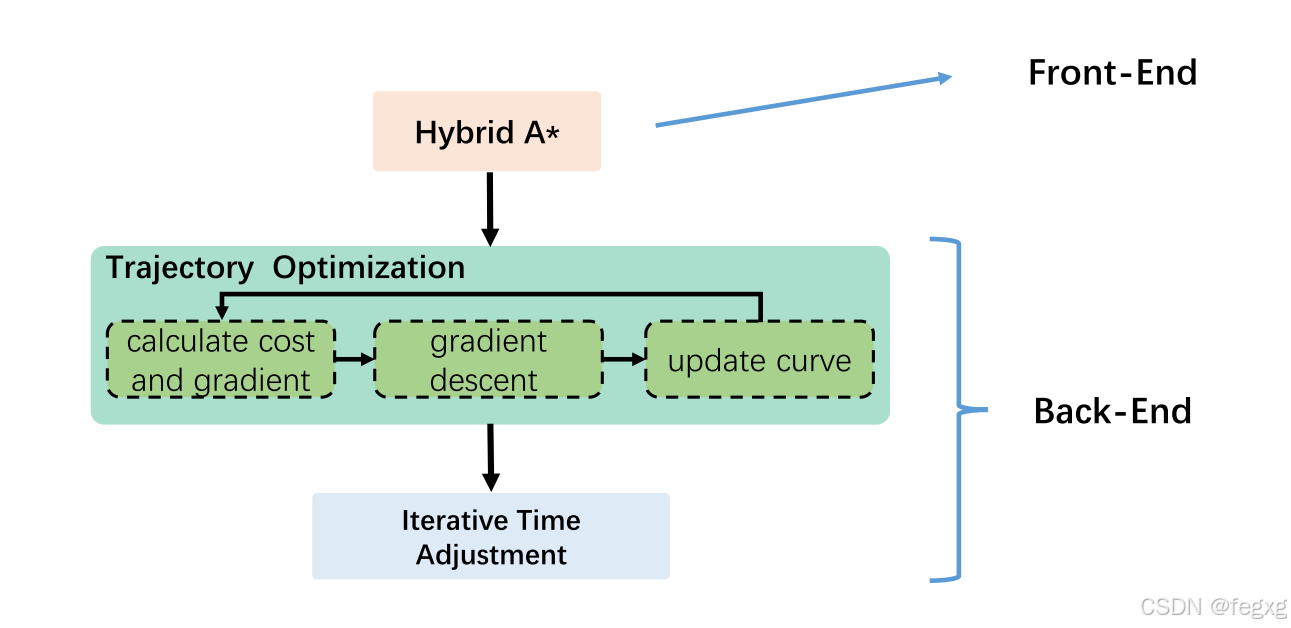
前端采用Hybrid A*算法初步搜索出一条路径，进入后端使用软约束优化得到优化好的B样条曲线，再将其表示为非均匀B样条的方式，调整控制点和时间间隔。

二、前端

1.算法架构

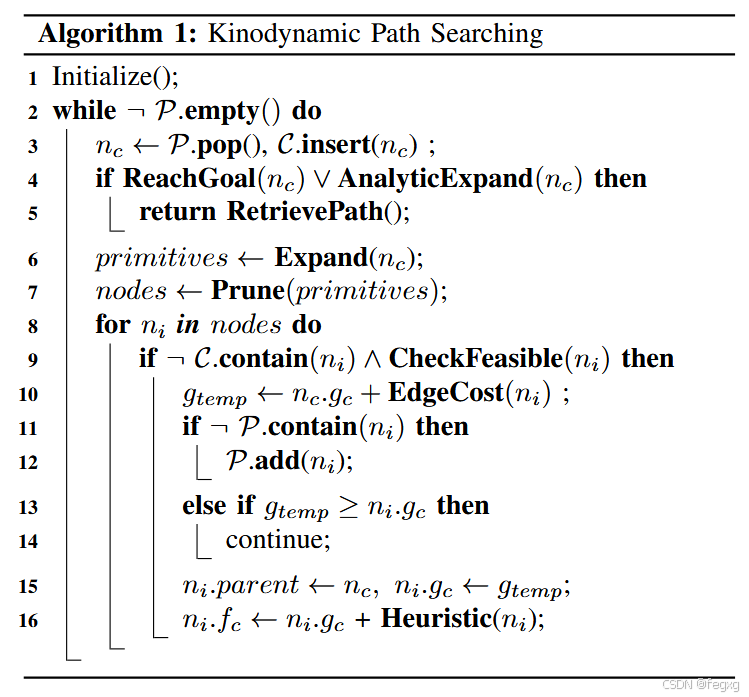
        前端的kinodynamic path searching使用hybrid A*算法，在地图中搜索出一条安全的、动力学的可行轨迹，算法流程如下：

2.图搜索算法

        首先我们说明图搜索算法的思路：

图搜索算法本质上是在维护一个容器，里面装着未来可能访问的节点，开始为容器里面节点数量为0，然后放入第一个节点进行循环，在循环中：

1.把容器中最符合条件的节点找到并访问弹出

2.将这个节点对周围的节点进行扩展

3.将扩展的新节点放入容器中

        同时，为了防止节点被反复循环，还需要另外一个容器装载被访问的节点，后面搜索时不能再进行访问。

        在这个架构下我们分析经典的基于搜索的算法：

Dijkstra算法每次弹出容器中距离源节点代价最小的节点（距离源节点的代价我们使用g来表示）。

A*算法容器的代价函数记作f，其由两个部分组成，第一个部分是g，即从源节点到当前节点累计代价，第二个部分是h，h代表启发式Heuristic代价，f=g+h。对于h的衡量有多种选择，如L2距离、曼哈顿距离等。

        在原本的A*算法下，hybrid A*不同于启发式函数和动力学可行kinodynamic。在这里采用离散输入量的办法，输入量为加速度a，则位置p可以表示为：

        在a的范围内进行离散采样，根据初始位置和速度可以算出该采样输入a作用下转移的新状态，由此拓展出新的节点来，并且是动力学可行的。

3.代码架构

对于这里的算法结构

首先说明其中的变量含义：

P为开集，即优先级队列，C为闭集，即已经进行扩展后的节点容器，nc为优先级队列中队首元素，nodes为拓展出的周围节点，primitives是离散输入作用的一段位移，gc为代价g，fc为总的代价f，整个流程为：

这里对应fast planner中的代码为：path_searching/src/kinodynamic_astar.cpp

int KinodynamicAstar::search(Eigen::Vector3d start_pt, Eigen::Vector3d start_v, Eigen::Vector3d start_a,
                             Eigen::Vector3d end_pt, Eigen::Vector3d end_v, bool init, bool dynamic, double time_start)//A*搜索
{
  start_vel_ = start_v;
  start_acc_ = start_a;//设置起始点的速度和加速度

  PathNodePtr cur_node = path_node_pool_[0];//当前节点nc
  cur_node->parent = NULL;//父节点为空
  cur_node->state.head(3) = start_pt;//当前节点的位置
  cur_node->state.tail(3) = start_v;//当前节点的速度
  cur_node->index = posToIndex(start_pt);//将三维位置转化至栅格地图的index
  cur_node->g_score = 0.0;//当前节点的gc，即从起点到当前节点的cost，这里起点为0

  Eigen::VectorXd end_state(6);
  Eigen::Vector3i end_index;
  double time_to_goal;

  end_state.head(3) = end_pt;
  end_state.tail(3) = end_v;
  end_index = posToIndex(end_pt);
  cur_node->f_score = lambda_heu_ * estimateHeuristic(cur_node->state, end_state, time_to_goal);//计算启发式代价，初始点的fc总代价就是启发式代价，因为gc为0
  cur_node->node_state = IN_OPEN_SET;//当前节点的状态，一共两种，OPEN和CLOSED，在CLOSED中的节点是已经访问过的
  open_set_.push(cur_node);//OPEN加入当前节点，即优先级队列
  use_node_num_ += 1;

  if (dynamic)//为节点附加时间维度信息，动态搜索情况
  {
    time_origin_ = time_start;//记录起始时间
    cur_node->time = time_start;
    cur_node->time_idx = timeToIndex(time_start);//转换时间索引
    expanded_nodes_.insert(cur_node->index, cur_node->time_idx, cur_node);//将 (index, time_idx) 插入到 expanded_nodes_ 中，expanded_nodes_存储已访问节点的集合
    // cout << "time start: " << time_start << endl;//使用 (index, time_idx) 作为键值对，确保同一空间位置在不同时间点可以有不同的状态
  }
  else
    expanded_nodes_.insert(cur_node->index, cur_node);//否则将用空间位置索引来记录，静态情况

  PathNodePtr neighbor = NULL;
  PathNodePtr terminate_node = NULL;
  bool init_search = init;
  const int tolerance = ceil(1 / resolution_);

  while (!open_set_.empty())//主循环，优先级队列不为空
  {
    cur_node = open_set_.top();//弹出队首元素为当前节点nc

    // Terminate?
    bool reach_horizon = (cur_node->state.head(3) - start_pt).norm() >= horizon_;//接近边界
    bool near_end = abs(cur_node->index(0) - end_index(0)) <= tolerance &&
                    abs(cur_node->index(1) - end_index(1)) <= tolerance &&
                    abs(cur_node->index(2) - end_index(2)) <= tolerance;//解决目标节点

    if (reach_horizon || near_end)//如果某一个满足
    {
      terminate_node = cur_node;//当前节点为结束节点
      retrievePath(terminate_node);//从结束节点开始向后倒退得到路径
      if (near_end)
      {
        // Check whether shot traj exist
        estimateHeuristic(cur_node->state, end_state, time_to_goal);//计算启发式函数，主要得到optimal_time
        computeShotTraj(cur_node->state, end_state, time_to_goal);//根据这个optimal_time来计算能否直接生成一条动力学可行的路直接连接到目标点
        if (init_search)//如果是初始搜索，会报错，在初始搜索阶段，如果能够直接从起点生成一条连接到目标点的轨迹（shot trajectory），通常是不合理的
          ROS_ERROR("Shot in first search loop!");
      }
    }
    if (reach_horizon)//处理各种情况
    {
      if (is_shot_succ_)
      {
        std::cout << "reach end" << std::endl;
        return REACH_END;
      }
      else
      {
        std::cout << "reach horizon" << std::endl;
        return REACH_HORIZON;
      }
    }

    if (near_end)
    {
      if (is_shot_succ_)
      {
        std::cout << "reach end" << std::endl;
        return REACH_END;
      }
      else if (cur_node->parent != NULL)
      {
        std::cout << "near end" << std::endl;
        return NEAR_END;
      }
      else
      {
        std::cout << "no path" << std::endl;
        return NO_PATH;
      }
    }
    open_set_.pop();//弹出当前节点
    cur_node->node_state = IN_CLOSE_SET;//将当前节点加入CLOSED集合，已访问过的节点集合
    iter_num_ += 1;//迭代次数加1

    double res = 1 / 2.0, time_res = 1 / 1.0, time_res_init = 1 / 20.0;//输入进行离散化，r取2，则对应5个离散后的输入量，
    Eigen::Matrix<double, 6, 1> cur_state = cur_node->state;//当前的状态，位置和速度共6维
    Eigen::Matrix<double, 6, 1> pro_state;//扩展后的节点状态
    vector<PathNodePtr> tmp_expand_nodes;//临时存