第5章 密集线性问题和分解 (本文由微软Copilot - Think Deeper辅助完成)
1. 向量空间
1.1. 向量空间示例
1.2. 向量积
1.2.1 点积
1.2.2 哈达马德积(舒尔积)
1.2.3 克罗内克积
2. 线性方程
2.1. 矩阵乘法的直觉
2.2. 解集
2.3. 欠定系统
2.4. 超定系统
2.5. 定解
2.6. 齐次与非齐次
3. 解线性方程
3.1. 使用奇异值分解(SVD)
3.2. 完全正交分解
3.3. 使用QR分解
3.4. 使用Cholesky分解
3.5. 高斯消元法(行简化)3.5.1. 前向消元
3.5.2. 前向和后向代换
3.5.3. 部分选主和全选主
3.5.4. 高斯消元法的数值稳定性
3.5.5. 高斯消元算法示例
3.5.6. 行阶梯形
3.5.7. 简化行阶梯形
3.5.8. 行阶梯形示例
3.5.9. 阶梯枢轴列
4. 矩阵分解
4.1. QR分解
4.1.1. 方阵QR分解
4.1.2. 矩形矩阵QR分解
4.2. 计算QR分解
4.3. 格拉姆-施密特正交化
4.4. Householder变换
4.5. QL,RQ和LQ分解
4.6. Cholesky分解LL*
4.7. 厄米特矩阵
4.8. 正定(半定)矩阵
4.9. LDL分解
4.10. 下三角上三角(LU)分解
4.11. 下三角对角上三角(LDU)分解
4.12. 特征值和特征向量
4.13. 计算特征值和特征向量
4.13.1 计算特征值和特征向量的示例
4.14. 矩阵的特征分解
4.15. 奇异值分解
4.15.1 奇异值分解的应用
4.15.1.1 伪逆
4.15.1.2 解齐次线性方程
4.15.1.3 值域,零空间和秩
4.15.1.4 最近的正交矩阵
5. 线性映射
6. 张量
7. 子空间
7.1. 行空间和列空间
8. 矩阵的值域
8.1. 行空间示例
9. 基
9.1. 计算列空间基的示例
9.2. 计算行空间基的示例
9.3. 基向量的变化
9.4. 向量的协变和逆变
9.5. 创建基集合
9.6. 基的变化
9.7. 向量场
9.8. 坐标系
9.8.1. 笛卡尔、极坐标、曲线坐标、圆柱坐标和球坐标
9.9. 坐标变换
9.10. 仿射和曲线变换
10. 矩阵的秩
10.1. 计算秩的结论
11. 列空间的维度
12. 零空间(核)
12.1. 计算零空间的示例
13. 零度
14. 秩-零度定理
15. 矩阵的行列式
16. 求矩阵的逆
17. 线性代数基本定理
18. 置换矩阵
19. 增广矩阵
1. 向量空间
向量空间是一个由向量组成的集合,配备了两个满足特定公理的运算:向量加法和标量乘法。在这个空间中,向量可以进行加法运算,也可以被标量(通常为实数或复数)所乘,以得到新的向量。
向量空间满足以下八个公理,其中 VV 是向量集合, FF 是数域(例如实数域 RR 或复数域 CC)。

1.1 向量空间的例子
为了更直观地理解向量空间,我们来看一些具体的例子。


#include <iostream>
#include <Eigen/Dense>
intmain(){
// 定义二维向量 v1 和 v2
Eigen::Vector2d v1(1.0,2.0);
Eigen::Vector2d v2(3.0,4.0);
// 向量加法
Eigen::Vector2d v_sum = v1 + v2;
// 标量乘法
double scalar =2.0;
Eigen::Vector2d v_scaled = scalar * v1;
// 输出结果
std::cout <<"向量 v1: \n"<< v1 <<"\n\n";
std::cout <<"向量 v2: \n"<< v2 <<"\n\n";
std::cout <<"v1 + v2 = \n"<< v_sum <<"\n\n";
std::cout <<"2 * v1 = \n"<< v_scaled <<"\n";
return0;
}代码详解:
包含头文件:
#include <iostream> // 标准输入输出库 #include <Eigen/Dense> // Eigen 库,用于线性代数运算定义主函数:
int main() { // ...代码... return 0; }定义向量:
Eigen::Vector2d v1(1.0, 2.0); Eigen::Vector2d v2(3.0, 4.0);Eigen::Vector2d表示 2 维双精度(double)向量。
向量加法和标量乘法:
Eigen::Vector2d v_sum = v1 + v2; Eigen::Vector2d v_scaled = scalar * v1;v_sum是向量加法的结果。
v_scaled是标量乘法的结果。
输出结果:
std::cout <<"向量 v1: \n"<< v1 <<"\n\n"; std::cout <<"向量 v2: \n"<< v2 <<"\n\n"; std::cout <<"v1 + v2 = \n"<< v_sum <<"\n\n"; std::cout <<"2 * v1 = \n"<< v_scaled <<"\n";
运行结果:
向量 v1:
1
2
向量 v2:
3
4
v1 + v2 =
4
6
2 * v1 =
2
41.2 向量积
向量积是指向量之间的乘法运算,根据运算方式的不同,结果可能是标量或新向量。
1.2.1 点积
点积(内积)是两个向量对应分量相乘后再求和的运算,结果为一个标量。
公式:

示例代码:
#include <iostream>
#include <Eigen/Dense>
intmain(){
// 定义三个维度的向量 u 和 v
Eigen::Vector3d u(1.0,2.0,3.0);
Eigen::Vector3d v(4.0,5.0,6.0);
// 计算点积
double dot = u.dot(v);
// 输出结果
std::cout <<"向量 u: \n"<< u <<"\n\n";
std::cout <<"向量 v: \n"<< v <<"\n\n";
std::cout <<"u ⋅ v = "<< dot <<"\n";
return0;
}代码详解:
u.dot(v)计算向量
u和v的点积。
运行结果:
向量 u:
1
2
3
向量 v:
4
5
6
u ⋅ v = 32计算:

1.2.2 哈达玛积(舒尔积)
哈达玛积(Hadamard 积)是两个同维度向量对应元素相乘,得到新的向量。

示例代码:
#include <iostream>
#include <Eigen/Dense>
intmain(){
// 定义向量 s 和 t
Eigen::Vector2d s(1.0,2.0);
Eigen::Vector2d t(3.0,4.0);
// 计算哈达玛积
Eigen::Vector2d hadamard = s.array()* t.array();
// 输出结果
std::cout <<"向量 s: \n"<< s <<"\n\n";
std::cout <<"向量 t: \n"<< t <<"\n\n";
std::cout <<"s ⊙ t = \n"<< hadamard <<"\n";
return0;
}代码详解:
s.array()将向量视为数组,以便进行按元素的操作。
*运算符用于数组的逐元素乘法。
运行结果:
向量 s:
1
2
向量 t:
3
4
s ⊙ t =
3
81.2.3 克罗内克积
克罗内克积(Kronecker 积)是矩阵之间的张量积,结果是一个更大的矩阵。

示例代码:
#include <iostream>
#include <Eigen/Dense>
intmain(){
// 定义矩阵 A 和 B
Eigen::Matrix2d A;
Eigen::Matrix2d B;
A <<1,2,
3,4;
B <<0,5,
6,7;
// 计算克罗内克积
Eigen::MatrixXd kron =Eigen::kroneckerProduct(A, B).eval();
// 输出结果
std::cout <<"矩阵 A: \n"<< A <<"\n\n";
std::cout <<"矩阵 B: \n"<< B <<"\n\n";
std::cout <<"A ⊗ B = \n"<< kron <<"\n";
return0;
}代码详解:
Eigen::kroneckerProduct(A, B)计算克罗内克积。
eval()用于强制计算结果,以确保后续输出正确。
运行结果:
矩阵 A:
1 2
3 4
矩阵 B:
0 5
6 7
A ⊗ B =
0 5 0 10
6 7 12 14
0 15 0 20
18 21 24 28总结
通过以上内容,我们深入了解了向量空间的定义和公理,同时探讨了向量空间的具体例子。我们还介绍了向量乘积的不同类型,包括点积、哈达玛积和克罗内克积,并通过代码示例演示了如何计算和应用这些运算。
延伸阅读:
- 线性映射与矩阵表示
:了解向量空间之间的线性映射及其矩阵表示。
- 基与维度
:学习向量空间的基的概念,以及如何确定向量空间的维度。
- 内积空间
:深入探讨具有内积结构的向量空间,即赋予向量空间长度和角度的概念。
向量空间是线性代数的核心概念,广泛应用于物理学、工程学、计算机科学等领域。理解向量空间及其运算,对于深入学习和应用线性代数至关重要。
2. 线性方程

解析:这意味着我们将系数、未知数和常数项分别组合成矩阵和向量的形式,利用矩阵运算的简洁性,方便求解和分析。这种表示方法在工程、物理、计算机科学(例如计算机图形学、机器学习中的回归问题)等领域尤为重要。
2.1 矩阵乘法的直观理解
矩阵乘法可以被视为向量的线性组合。具体来说,矩阵与向量相乘,相当于用向量的各个分量对矩阵的列进行加权,然后将结果相加。

2.2 解集的可能性
一个线性方程组可能存在以下三种情况之一:
- 无数个解
:当方程组具有自由度,未知数多于独立方程数量,且方程彼此不矛盾。
- 唯一解
:当方程数量等于未知数数量,且方程组满秩(矩阵 AA 可逆)。
- 无解
:当方程组存在矛盾,无法找到同时满足所有方程的解。
解集的情况取决于方程与未知数的数量以及方程之间的独立性。
2.3 欠定系统
当方程数量少于未知数数量时,称为欠定系统。在这种情况下:
如果方程不矛盾,通常存在无数个解(无限解)。
如果方程矛盾,则无解。
2.4 超定系统
当方程数量多于未知数数量时,称为超定系统。在这种情况下:
方程可能矛盾,导致无解。
若方程近似一致,可以通过最小二乘法找到一个近似解,使得误差平方和最小。
2.5 适定系统
当方程数量等于未知数数量时,称为适定系统。在这种情况下:
如果矩阵 AA 满秩(可逆),则存在唯一解。
如果矩阵 AA 不满秩,则可能存在无数个解或无解。
根据具体情况,可选择不同的求解方法,平衡速度与精度。
2.6 齐次与非齐次方程组

2.7 线性方程组的求解方法
为了具体展示线性方程组的求解过程,我们将使用 C++ 和 Eigen 库编写代码,并添加详细的注释。
示例代码:求解线性方程组
#include <iostream>
#include <Eigen/Dense>
intmain(){
// 定义一个 3x3 的矩阵 A,系数矩阵
Eigen::Matrix3f A;
A <<1,2,3, // 第一行元素:a_{11}, a_{12}, a_{13}
4,5,6, // 第二行元素:a_{21}, a_{22}, a_{23}
7,8,10;// 第三行元素:a_{31}, a_{32}, a_{33}
// 定义一个 3x1 的向量 b,常数项
Eigen::Vector3f b;
b <<6,15,25;// 常数项 b_1, b_2, b_3
// 输出矩阵 A 和向量 b
std::cout <<"系数矩阵 A:\n"<< A << std::endl;
std::cout <<"常数向量 b:\n"<< b << std::endl;
// 使用 PartialPivLU 分解求解 Ax = b
Eigen::Vector3f x = A.partialPivLu().solve(b);
// 输出解 x
std::cout <<"方程组的解 x:\n"<< x << std::endl;
return0;
}代码详解:
包含必要的头文件:
#include <iostream> // 用于标准输入输出 #include <Eigen/Dense> // 包含 Eigen 库的密集矩阵相关功能主函数:
int main() { // ... 代码 ... return 0; }定义系数矩阵 A:
Eigen::Matrix3f A; A << 1, 2, 3, 4, 5, 6, 7, 8, 10;
Eigen::Matrix3f表示 3x3 的浮点矩阵。
使用逗号初始化器
<<按行填充矩阵元素。
定义常数向量 b:
Eigen::Vector3f b;
b << 6, 15, 25;Eigen::Vector3f表示 3x1 的浮点向量。
填充常数项。
输出矩阵 A 和向量 b:
std::cout << "系数矩阵 A:\n" << A << std::endl;
std::cout << "常数向量 b:\n" << b << std::endl;使用
std::cout输出矩阵和向量。
求解线性方程组:
Eigen::Vector3f x = A.partialPivLu().solve(b);partialPivLu():对矩阵 A 进行部分主元 LU 分解,数值稳定性较好。
solve(b):求解方程组 Ax=b
。
输出解 x:
std::cout << "方程组的解 x:\n" << x << std::endl;输出求得的未知数向量 x。
运行结果:
系数矩阵 A:
1 2 3
4 5 6
7 8 10
常数向量 b:
6
15
25
方程组的解 x:
1
1
1
2.8 不同求解方法的比较
在求解线性方程组时,根据系数矩阵的性质和精度要求,可以选择不同的方法:
直接求逆(不推荐):
Eigen::Vector3f x = A.inverse() * b;
- 缺点
:计算矩阵逆存在数值不稳定性和较高的计算代价。
- 建议
:除非矩阵非常小且条件数较好,否则不推荐直接求逆。
LU 分解:
Eigen::Vector3f x = A.lu().solve(b);- 适用场景
:一般情况下,LU 分解速度快,适用于方阵。
QR 分解:
Eigen::Vector3f x = A.householderQr().solve(b);- 适用场景
:适用于非方阵或接近奇异的矩阵。
最小二乘法(适用于超定方程组):
Eigen::VectorXf x = A.colPivHouseholderQr().solve(b);- 适用场景
:当方程数量多于未知数数量,需要找到误差最小的近似解。
Cholesky 分解(适用于正定矩阵):
Eigen::Vector3f x = A.ldlt().solve(b);- 适用场景
:系数矩阵对称且正定,计算效率高。
2.9 线性方程组的数值稳定性
在实际计算中,系数矩阵的条件数会影响求解结果的精度:
- 条件数大
(矩阵接近奇异):求解结果对输入数据和舍入误差非常敏感,可能产生较大误差。
- 条件数小
(矩阵较好):求解结果对误差不敏感,计算结果可靠。
建议:
- 避免直接求逆
:使用矩阵分解方法求解,数值稳定性更好。
- 使用高精度数据类型
:在精度要求高的计算中,考虑使用
double或更高精度的数据类型。
2.10 总结与展望
线性方程组是数学、物理和工程中的基本问题,理解其求解方法对于各种应用都至关重要。通过矩阵形式表示,可以利用计算机和高效的数值算法快速求解。此外,理解矩阵的性质(如秩、条件数)也有助于选择合适的求解方法,提高计算的准确性和效率。
进一步阅读:
- 矩阵秩与解的唯一性
:了解矩阵的秩如何影响线性方程组的解的存在性和唯一性。
- 稀疏矩阵的求解
:在大型稀疏矩阵的情况下,使用专门的算法可以大大提高计算效率。
- 迭代方法
:如共轭梯度法、Jacobi 法等,适用于大型线性系统的求解。
参考资料:
- Eigen 官方文档
:https://eigen.tuxfamily.org/index.php?title=Main_Page
- 《线性代数及其应用》
,Gilbert Strang 著
- 《数值线性代数》
,Trefethen & Bau 著
3. 求解线性方程
3.1 使用奇异值分解(SVD)
如果您需要求解最小二乘问题,但对奇异值分解本身不感兴趣,那么一种更快速的替代方法是使用完全正交分解。
#include <iostream>
#include <Eigen/Dense>
intmain(){
// 生成一个随机的 3x2 浮点数矩阵 A
Eigen::MatrixXf A = Eigen::MatrixXf::Random(3,2);
std::cout <<"矩阵 A:\n"<< A << std::endl;
// 生成一个随机的 3x1 浮点数向量 b
Eigen::VectorXf b = Eigen::VectorXf::Random(3);
std::cout <<"右侧向量 b:\n"<< b << std::endl;
// 使用奇异值分解求解最小二乘问题 Ax = b
Eigen::VectorXf x = A.bdcSvd(Eigen::ComputeThinU | Eigen::ComputeThinV).solve(b);
std::cout <<"最小二乘解 x:\n"<< x << std::endl;
return0;
}代码详解:
包含必要的头文件:
#include <iostream> #include <Eigen/Dense>主函数
main():int main() { // ...代码... return 0; }生成随机矩阵 A:
Eigen::MatrixXf A = Eigen::MatrixXf::Random(3, 2);MatrixXf:动态大小的单精度浮点矩阵。
Random(3, 2):生成一个 3 行 2 列的随机矩阵,元素取值范围在 [-1, 1]。
输出矩阵 A:
std::cout << "矩阵 A:\n" << A << std::endl;生成随机向量 b:
Eigen::VectorXf b = Eigen::VectorXf::Random(3);VectorXf:动态大小的单精度浮点列向量。
Random(3):生成一个 3 行的随机向量。
输出向量 b:
std::cout << "右侧向量 b:\n" << b << std::endl;使用奇异值分解求解最小二乘问题 Ax = b:
Eigen::VectorXf x = A.bdcSvd(Eigen::ComputeThinU | Eigen::ComputeThinV).solve(b);bdcSvd():对矩阵 A 进行双对角化奇异值分解(Bidiagonal SVD)。
Eigen::ComputeThinU | Eigen::ComputeThinV:计算精简的奇异值分解,只计算必要的部分,以提高计算效率。
solve(b):求解最小二乘问题。
输出解 x:
std::cout << "最小二乘解 x:\n" << x << std::endl;
3.2 完全正交分解

完全正交分解的优势在于它能准确地揭示矩阵的秩,进而用于解决最小二乘问题,特别是在矩阵可能秩亏的情况下。
3.3 使用 QR 分解
在 QR 分解类中,solve() 方法也可以用来计算最小二乘解。Eigen 提供了三种 QR 分解类:
HouseholderQR:
- 无主元选择
,速度最快。
如果矩阵不是满秩,则数值上 不稳定。
ColPivHouseholderQR:
- 列主元选择
,稍微慢一些。
比
HouseholderQR更稳定,适用于大多数情况。
FullPivHouseholderQR:
- 全主元选择
(同时进行行和列的主元选择),速度最慢。
比
ColPivHouseholderQR稍微更稳定,适用于矩阵可能秩亏的情况。
示例代码:
#include <iostream>
#include <Eigen/Dense>
intmain(){
// 生成一个随机的 3x2 浮点数矩阵 A
Eigen::MatrixXf A = Eigen::MatrixXf::Random(3,2);
// 生成一个随机的 3x1 浮点数向量 b
Eigen::VectorXf b = Eigen::VectorXf::Random(3);
// 使用列主元 Householder QR 分解求解最小二乘问题
Eigen::VectorXf x = A.colPivHouseholderQr().solve(b);
std::cout <<"使用 QR 分解求解的解 x:\n"<< x << std::endl;
return0;
}代码详解:
与之前的代码类似,生成随机矩阵 A 和向量 b。
使用
colPivHouseholderQr()方法对 A 进行列主元 Householder QR 分解。调用
solve(b)求解最小二乘问题。
3.4 使用乔利斯基分解

示例代码:
#include <iostream>
#include <Eigen/Dense>
intmain(){
// 生成一个随机的 3x2 浮点数矩阵 A
Eigen::MatrixXf A = Eigen::MatrixXf::Random(3,2);
// 生成一个随机的 3x1 浮点数向量 b
Eigen::VectorXf b = Eigen::VectorXf::Random(3);
// 计算 A 的转置乘以 A
Eigen::MatrixXf AtA = A.transpose()* A;
// 计算 A 的转置乘以 b
Eigen::VectorXf Atb = A.transpose()* b;
// 使用 LDLT 分解求解正规方程
Eigen::VectorXf x = AtA.ldlt().solve(Atb);
std::cout <<"使用正规方程求解的解 x:\n"<< x << std::endl;
return0;
}代码详解:

求解器比较
下面的代码比较了三种不同求解方法的速度:直接求逆、QR 分解和乔利斯基分解。
#include <iostream>
#include <Eigen/Dense>
#include <ctime>
#define MATRIX_SIZE 100
intmain(){
// 使用命名空间
usingnamespace Eigen;
usingnamespace std;
// 生成一个随机的 MATRIX_SIZE x MATRIX_SIZE 的矩阵
MatrixXd matrix_NN =MatrixXd::Random(MATRIX_SIZE, MATRIX_SIZE);
// 确保矩阵为正定矩阵(对称且特征值为正)
matrix_NN = matrix_NN * matrix_NN.transpose();
// 生成一个随机的向量
VectorXd v_Nd =VectorXd::Random(MATRIX_SIZE);
// 计时器
clock_t time_stt =clock();
// 方法一:直接求逆
VectorXd x = matrix_NN.inverse()* v_Nd;
cout <<"======================= 直接求逆耗时: "
<<1000*(clock()- time_stt)/(double)CLOCKS_PER_SEC
<<" 毫秒 ======================= "<< endl;
// 方法二:使用 QR 分解
time_stt =clock();
x = matrix_NN.colPivHouseholderQr().solve(v_Nd);
cout <<"======================= QR 分解耗时: "
<<1000*(clock()- time_stt)/(double)CLOCKS_PER_SEC
<<" 毫秒 ======================= "<< endl;
// 方法三:使用乔利斯基分解
time_stt =clock();
x = matrix_NN.ldlt().solve(v_Nd);
cout <<"======================= 乔利斯基分解耗时: "
<<1000*(clock()- time_stt)/(double)CLOCKS_PER_SEC
<<" 毫秒 ======================= "<< endl;
return0;
}代码详解:
定义矩阵大小
MATRIX_SIZE,这里为 100。生成随机正定矩阵 matrix_NN。
生成随机向量 v_Nd。
使用
clock()计时。
三个方法的比较:
直接求逆:
计算
matrix_NN.inverse() * v_Nd。缺点:计算逆矩阵耗时且数值不稳定。
QR 分解:
使用
colPivHouseholderQr().solve(v_Nd)。优点:比直接求逆更快且稳定。
乔利斯基分解:
使用
ldlt().solve(v_Nd)。优点:对于正定矩阵,这是最快的方法。
结果展示每种方法的耗时,您可以运行代码查看实际差异。
3.5 高斯消元法(行化简)
3.5.1 矩阵的秩
高斯消元法(行化简)可用于求解线性方程组。它通过一系列 初等行变换,将矩阵转换为 行阶梯形矩阵,即左下角全为零的形式。
初等行变换包括:
- 交换两行。
- 将某一行乘以一个非零常数。
- 将某一行的倍数加到另一行上。
高斯消元法也可用于计算:
- 矩阵的秩。
- 方阵的行列式。
- 可逆矩阵的逆。
3.5.2 前向消元与回代

- 下三角矩阵(L):
从上到下依次求解,每一步都只含有一个新的未知数,称为前向替换。
- 上三角矩阵(U):
从下到上依次求解,每一步都只含有一个新的未知数,称为回代。
3.5.3 部分选主元法和全选主元法
部分选主元法:
在消元过程中,每一步选择当前列中 绝对值最大 的元素作为主元,并交换行。
目的:避免主元过小导致数值不稳定。
全选主元法:
在消元过程中,每一步在剩余的子矩阵中选择 绝对值最大 的元素作为主元,并同时交换行和列。
适用于提高数值稳定性的情况。
3.5.4 高斯消元法中的数值稳定性
在高斯消元法中,如果主元为零或非常小,会导致消元失败或数值不稳定。例如:
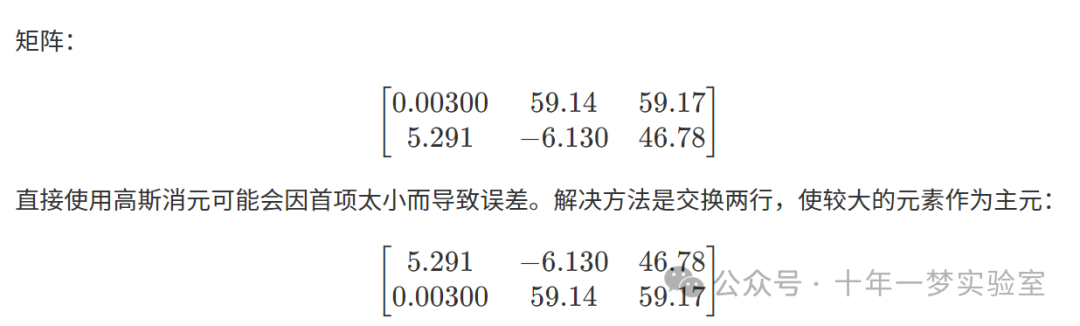
3.5.5 高斯消元算法示例

3.5.6 行阶梯形
经过高斯消元后,矩阵处于 行阶梯形 状态,具有以下特征:
所有仅由零组成的行位于矩阵的底部。
每个非零行的首项(第一个非零元素)位于其上方行的首项的右侧。
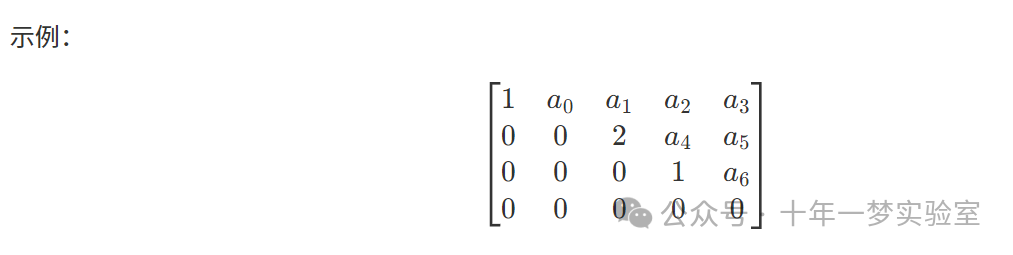
3.5.7 简化行阶梯形(行最简形)
如果一个行阶梯形矩阵满足:
每个非零行的首项为 1(称为首 1)。
每个首 1 所在列的其他元素为 0。
那么该矩阵就是 简化行阶梯形。

特性:
- 简化行阶梯形是唯一的
,即对于给定矩阵,其简化行阶梯形是确定的。
3.5.8 阶梯形示例

3.5.9 阶梯形主元列
在行阶梯形中:
每个非零行的首项所在的列称为 主元列。
主元列的位置从左到右依次增加。
参考文献
[1] Eigen 官方文档:https://eigen.tuxfamily.org/dox/group__LeastSquares.html
4. 矩阵分解
根据矩阵的特点,你可以在各种分解方法中进行选择,这取决于你更倾向于速度还是精度。
4.1 QR分解
4.1.1. 方阵QR分解

4.1.2. 长方矩阵QR分解

4.2 计算QR分解
要计算矩阵的QR分解,我们可以使用多种算法,其中最常用的是格拉姆-施密特正交化、豪斯霍尔德变换和吉文斯旋转。下面,我们将介绍这些方法,并通过C++代码实例进行说明。
4.3 格拉姆 - 施密特正交化
格拉姆 - 施密特过程是一种对一组向量进行正交归一化的方法。在这个过程中,要使每一列向量与它前面的列向量都垂直。

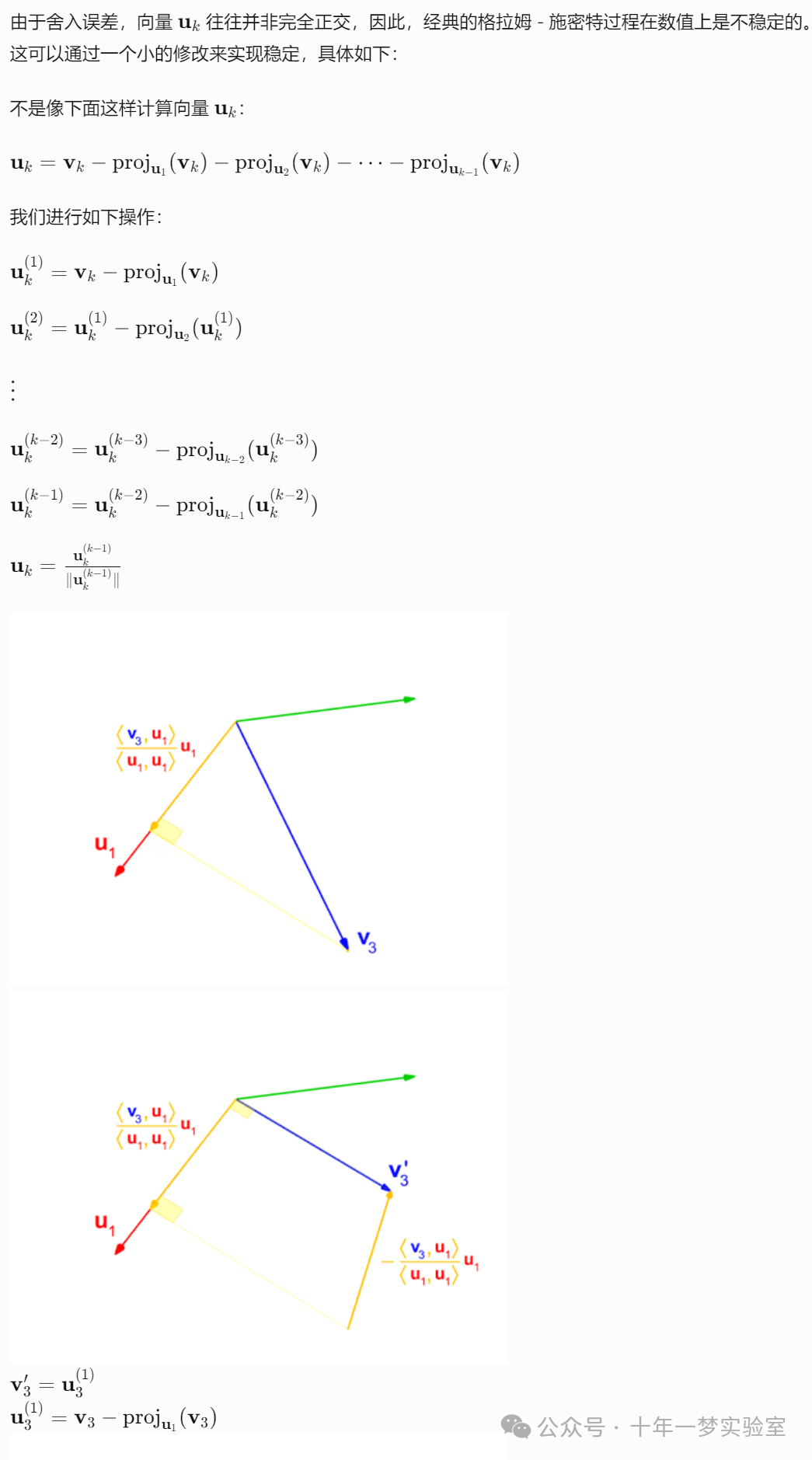


实现代码(C++语言):
下面,我们将使用C++实现格拉姆 - 施密特正交化算法,并添加详细的注释。
#include <iostream>
#include <vector>
#include <cmath>
// 定义类型别名,方便代码书写
typedef std::vector<double> Vector;
typedef std::vector<Vector> Matrix;
// 计算两个向量的内积
doubledotProduct(const Vector& v1,const Vector& v2){
double result =0.0;
for(size_t i =0; i < v1.size();++i){
result += v1[i]* v2[i];
}
return result;
}
// 计算向量的范数(即模)
doublenorm(const Vector& v){
return std::sqrt(dotProduct(v, v));
}
// 向量除以标量
Vector scalarDivide(const Vector& v,double scalar){
Vector result = v;
for(double& elem : result){
elem /= scalar;
}
return result;
}
// 向量减法
Vector vectorSubtract(const Vector& v1,const Vector& v2){
Vector result = v1;
for(size_t i =0; i < v1.size();++i){
result[i]-= v2[i];
}
return result;
}
// 向量乘以标量
Vector scalarMultiply(const Vector& v,double scalar){
Vector result = v;
for(double& elem : result){
elem *= scalar;
}
return result;
}
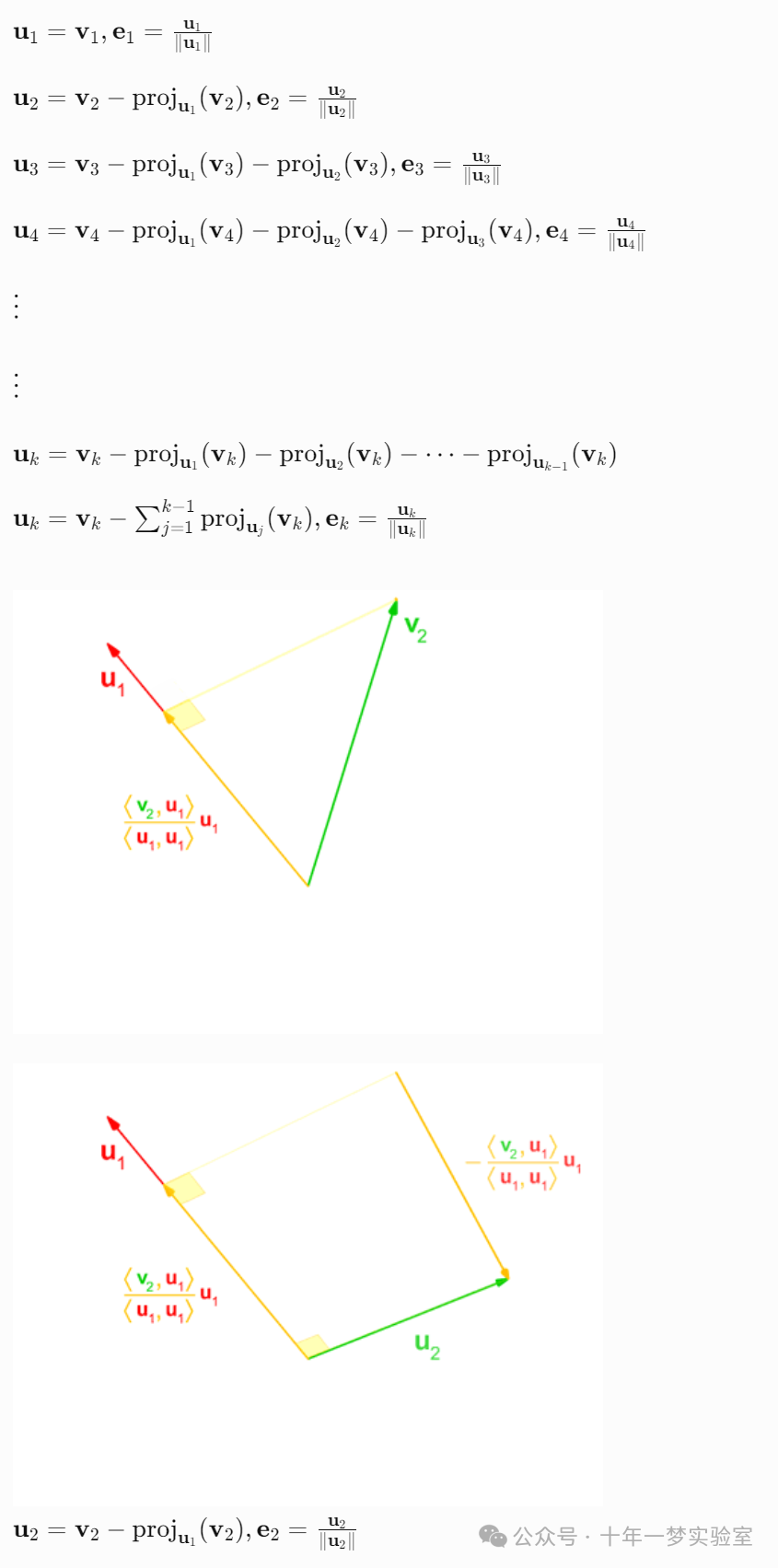
// 格拉姆 - 施密特正交化算法
voidgramSchmidt(const Matrix& A, Matrix& Q, Matrix& R){
size_t m = A.size(); // 行数
size_t n = A[0].size(); // 列数
// 初始化Q和R矩阵
Q =Matrix(m,Vector(n,0.0));
R =Matrix(n,Vector(n,0.0));
// 遍历每一列向量
for(size_t k =0; k < n;++k){
// 提取A的第k列向量
Vector v_k(m);
for(size_t i =0; i < m;++i){
v_k[i]= A[i][k];
}
Vector u_k = v_k;
// 对前面的列进行投影并从u_k中减去
for(size_t j =0; j < k;++j){
// 提取Q的第j列向量
Vector q_j(m);
for(size_t i =0; i < m;++i){
q_j[i]= Q[i][j];
}
// 计算R[j][k] = q_j^T * v_k
R[j][k]=dotProduct(q_j, v_k);
// u_k = u_k - R[j][k] * q_j
Vector temp =scalarMultiply(q_j, R[j][k]);
u_k =vectorSubtract(u_k, temp);
}
// 计算R[k][k] = ||u_k||
R[k][k]=norm(u_k);
// 计算q_k = u_k / R[k][k]
Vector q_k =scalarDivide(u_k, R[k][k]);
// 将q_k存入Q的第k列
for(size_t i =0; i < m;++i){
Q[i][k]= q_k[i];
}
}
}
// 打印矩阵
voidprintMatrix(const Matrix& M){
for(constauto& row : M){
for(double elem : row){
std::cout << elem <<"\t";
}
std::cout << std::endl;
}
}
intmain(){
// 示例矩阵A
Matrix A ={
{1,1,0},
{1,0,1},
{0,1,1}
};
Matrix Q, R;
// 进行格拉姆 - 施密特正交化
gramSchmidt(A, Q, R);
// 输出结果
std::cout <<"矩阵Q:"<< std::endl;
printMatrix(Q);
std::cout <<"\n矩阵R:"<< std::endl;
printMatrix(R);
return0;
}代码详解:
向量和矩阵操作函数:
dotProduct:计算两个向量的内积。
norm:计算向量的范数(模)。
scalarDivide:向量除以标量,实现归一化操作。
vectorSubtract:两个向量相减。
scalarMultiply:向量乘以标量。
Gram-Schmidt函数
gramSchmidt:输入:矩阵A,输出:正交矩阵Q和上三角矩阵R。
外层循环遍历每一列向量
v_k。内层循环计算投影并从
u_k中减去,即执行正交化过程。计算
R[k][k],即u_k的范数。归一化
u_k得到q_k,存入矩阵Q中。
主函数
main:定义示例矩阵A。
调用
gramSchmidt函数进行QR分解。输出矩阵Q和R。
运行结果:
矩阵Q:
0.707107 0 0.408248
0.707107 -0.57735 0.408248
0 0.816497 0.816497
矩阵R:
1.41421 0.707107 0.707107
0 1.22474 0.816497
0 0 1.22474验证结果:
我们可以验证

是否成立,可以在代码中增加以下代码:
// 矩阵乘法,用于验证A = QR
Matrix multiplyMatrix(const Matrix& M1,const Matrix& M2){
size_t rows = M1.size();
size_t cols = M2[0].size();
size_t inner = M2.size();
Matrix result(rows,Vector(cols,0.0));
for(size_t i =0; i < rows;++i){
for(size_t j =0; j < cols;++j){
for(size_t k =0; k < inner;++k){
result[i][j]+= M1[i][k]* M2[k][j];
}
}
}
return result;
}
...
// 验证A = QR
Matrix QR =multiplyMatrix(Q, R);
std::cout <<"\n验证A = QR:"<< std::endl;
printMatrix(QR);验证输出:
验证A = QR:
1 1 -1.11022e-16
1 -1.11022e-16 1
0 1 1由于浮点数精度,可能会出现极小的误差,但整体结果验证了
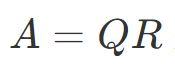
4.4 豪斯霍尔德变换
豪斯霍尔德变换是一种用于将矩阵转换为三角形形式的反射变换。它比格拉姆 - 施密特更稳定,计算效率也更高。

实现代码(C++语言):
#include <iostream>
#include <vector>
#include <cmath>
// ...(前面的代码保持不变,包括Matrix和Vector类型定义等)
// 生成单位矩阵
Matrix identityMatrix(size_t size){
Matrix I(size,Vector(size,0.0));
for(size_t i =0; i < size;++i){
I[i][i]=1.0;
}
return I;
}
// 豪斯霍尔德QR分解
voidhouseholderQR(const Matrix& A, Matrix& Q, Matrix& R){
size_t m = A.size();
size_t n = A[0].size();
Q =identityMatrix(m);
R = A;
for(size_t k =0; k < n;++k){
// 提取x向量
Vector x(m - k);
for(size_t i = k; i < m;++i){
x[i - k]= R[i][k];
}
// 计算豪斯霍尔德向量v
Vector e1(m - k,0.0);
e1[0]=1.0;
double alpha =(x[0]>=0)?-norm(x):norm(x);
Vector v =vectorSubtract(x,scalarMultiply(e1, alpha));
double v_norm =norm(v);
if(v_norm ==0)continue;
v =scalarDivide(v, v_norm);
// 构造H矩阵
Matrix H =identityMatrix(m);
for(size_t i = k; i < m;++i){
for(size_t j = k; j < m;++j){
H[i][j]-=2* v[i - k]* v[j - k];
}
}
// 更新R和Q
R =multiplyMatrix(H, R);
Q =multiplyMatrix(Q, H);
}
}
intmain(){
// 示例矩阵A
Matrix A ={
{2,4,1},
{3,2,5},
{1,3,2}
};
Matrix Q, R;
// 进行豪斯霍尔德QR分解
householderQR(A, Q, R);
// 输出结果
std::cout <<"矩阵Q:"<< std::endl;
printMatrix(Q);
std::cout <<"\n矩阵R:"<< std::endl;
printMatrix(R);
return0;
}代码详解:
豪斯霍尔德QR分解函数
householderQR:提取列向量 x。
构造豪斯霍尔德向量 v。
构造豪斯霍尔德矩阵 H。
更新 R 和 Q。
初始化 Q 为单位矩阵,R 为矩阵 A。
对于每一列 k,执行以下步骤:
运行结果:
矩阵Q:
-0.534522 -0.801784 -0.267261
-0.801784 0.597614 -0.0123079
-0.267261 -0.0123079 0.96309
矩阵R:
-3.74166 -5.87688 -4.00925
0 2.86138 1.94447
0 0 1.200964.5 QL、RQ和LQ分解
除了QR分解,还有其他类似的分解方法:
- QL分解
:将矩阵分解为一个正交矩阵和一个下三角矩阵的乘积。
- RQ分解
:将矩阵分解为一个上三角矩阵和一个正交矩阵的乘积。
- LQ分解
:将矩阵分解为一个下三角矩阵和一个正交矩阵的乘积。
这些分解在某些特定的应用中非常有用,例如在信号处理和数值分析中。
实现代码(以LQ分解为例):
#include <iostream>
#include <vector>
#include <cmath>
// ...(前面的代码保持不变,包括Matrix和Vector类型定义等)
// LQ分解基于QR分解
voidlqDecomposition(const Matrix& A, Matrix& L, Matrix& Q){
// 对A的转置进行QR分解,然后转置回来
Matrix A_T = A;// 复制A
size_t m = A.size();
size_t n = A[0].size();
// 转置A_T
for(size_t i =0; i < m;++i){
for(size_t j = i +1; j < n;++j){
std::swap(A_T[i][j], A_T[j][i]);
}
}
Matrix Q_T, R_T;
gramSchmidt(A_T, Q_T, R_T);// 可以使用之前实现的Gram-Schmidt函数
// 转置回去
L = R_T;
Q = Q_T;
// 转置L矩阵
for(size_t i =0; i < L.size();++i){
for(size_t j = i +1; j < L[0].size();++j){
std::swap(L[i][j], L[j][i]);
}
}
}
intmain(){
// 示例矩阵A
Matrix A ={
{1,2},
{3,4},
{5,6}
};
Matrix L, Q;
// 进行LQ分解
lqDecomposition(A, L, Q);
// 输出结果
std::cout <<"矩阵L:"<< std::endl;
printMatrix(L);
std::cout <<"\n矩阵Q:"<< std::endl;
printMatrix(Q);
return0;
}代码详解:
LQ分解函数
lqDecomposition:将矩阵 A 转置,得到 A_T。
对 A_T 进行 QR 分解。
将得到的 R_T 作为 L,Q_T 作为 Q。
转置 L,得到下三角矩阵。
4.6 乔列斯基分解 LL*
乔列斯基分解是将一个对称正定矩阵分解为一个下三角矩阵和其共轭转置的乘积:A=QR
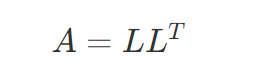
实现代码(C++语言):
#include <iostream>
#include <vector>
#include <cmath>
// ...(前面的代码保持不变,包括Matrix和Vector类型定义等)
// 乔列斯基分解
boolcholeskyDecomposition(const Matrix& A, Matrix& L){
size_t n = A.size();
L =Matrix(n,Vector(n,0.0));
for(size_t i =0; i < n;++i){
for(size_t j =0; j <= i;++j){
double sum =0.0;
if(j == i){// 对角线元素
for(size_t k =0; k < j;++k){
sum += L[j][k]* L[j][k];
}
double val = A[j][j]- sum;
if(val <=0){
// 不是正定矩阵,无法进行乔列斯基分解
returnfalse;
}
L[j][j]= std::sqrt(val);
}else{
for(size_t k =0; k < j;++k){
sum += L[i][k]* L[j][k];
}
L[i][j]=(A[i][j]- sum)/ L[j][j];
}
}
}
returntrue;
}
intmain(){
// 对称正定矩阵A
Matrix A ={
{6,15,55},
{15,55,225},
{55,225,979}
};
Matrix L;
// 进行乔列斯基分解
if(choleskyDecomposition(A, L)){
std::cout <<"下三角矩阵L:"<< std::endl;
printMatrix(L);
// 验证A = LL^T
Matrix LLT =multiplyMatrix(L,transposeMatrix(L));
std::cout <<"\n验证A = LL^T:"<< std::endl;
printMatrix(LLT);
}else{
std::cout <<"矩阵不是正定矩阵,无法进行乔列斯基分解。"<< std::endl;
}
return0;
}代码详解:
乔列斯基分解函数
choleskyDecomposition:输入:对称正定矩阵 A,输出:下三角矩阵 L。
嵌套循环计算 L 的元素,对角线元素和非对角线元素分开处理。
检查对角线元素的值是否大于零,以确保矩阵是正定的。
辅助函数
transposeMatrix:// 矩阵转置 Matrix transposeMatrix(const Matrix& M){ size_t rows = M.size(); size_t cols = M[0].size(); Matrix result(cols,Vector(rows,0.0)); for(size_t i =0; i < rows;++i){ for(size_t j =0; j < cols;++j){ result[j][i]= M[i][j]; } } return result; }
运行结果:
下三角矩阵L:
2.44949 0 0
6.12372 2.23607 0
22.4537 20.1246 6.32456
验证A = LL^T:
6 15 55
15 55 225
55 225 9794.7 埃尔米特矩阵

4.8 正定(半正定)矩阵

特征值条件:
正定矩阵的所有特征值都为正。
半正定矩阵的所有特征值都非负。
示例:
#include <iostream>
#include <vector>
#include <Eigen/Dense> // 使用Eigen库计算特征值
intmain(){
Eigen::Matrix3d M;
M <<2,-1,0,
-1,2,-1,
0,-1,2;
// 计算特征值
Eigen::SelfAdjointEigenSolver<Eigen::Matrix3d>eigensolver(M);
if(eigensolver.info()== Eigen::Success){
std::cout <<"特征值:"<< std::endl << eigensolver.eigenvalues()<< std::endl;
}else{
std::cout <<"计算特征值失败。"<< std::endl;
}
return0;
}运行结果:
特征值:
0.585786
2
3.41421所有特征值均为正,因此MM是正定矩阵。
4.9 LDL分解
LDL分解将一个对称矩阵分解为下三角矩阵、对角矩阵和下三角矩阵的转置的乘积:
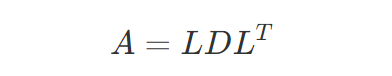
实现代码(C++语言):
#include <iostream>
#include <vector>
#include <cmath>
// ...(前面的代码保持不变,包括Matrix和Vector类型定义等)
boolldlDecomposition(const Matrix& A, Matrix& L, Matrix& D){
size_t n = A.size();
L =Matrix(n,Vector(n,0.0));
D =Matrix(n,Vector(n,0.0));
for(size_t i =0; i < n;++i){
// 初始化L的对角线元素
L[i][i]=1.0;
// 计算D[i][i]
double sum =0.0;
for(size_t k =0; k < i;++k){
sum += L[i][k]* L[i][k]* D[k][k];
}
D[i][i]= A[i][i]- sum;
// 计算L[i][j]
for(size_t j = i +1; j < n;++j){
sum =0.0;
for(size_t k =0; k < i;++k){
sum += L[j][k]* L[i][k]* D[k][k];
}
L[j][i]=(A[j][i]- sum)/ D[i][i];
}
}
returntrue;
}
intmain(){
// 示例矩阵A
Matrix A ={
{4,12,-16},
{12,37,-43},
{-16,-43,98}
};
Matrix L, D;
// 进行LDL分解
if(ldlDecomposition(A, L, D)){
std::cout <<"下三角矩阵L:"<< std::endl;
printMatrix(L);
std::cout <<"\n对角矩阵D:"<< std::endl;
printMatrix(D);
// 验证A = LDL^T
Matrix LD =multiplyMatrix(L, D);
Matrix LDLT =multiplyMatrix(LD,transposeMatrix(L));
std::cout <<"\n验证A = LDL^T:"<< std::endl;
printMatrix(LDLT);
}else{
std::cout <<"无法进行LDL分解。"<< std::endl;
}
return0;
}代码详解:
LDL分解函数
ldlDecomposition:输入:对称矩阵 A,输出:下三角矩阵 L,对角矩阵 D。
使用循环计算 L 和 D 的元素。
4.10 三角分解(LU分解)
LU分解将一个矩阵分解为一个下三角矩阵 LL 和一个上三角矩阵 UU 的乘积:
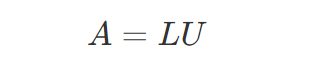
实现代码(C++语言):
#include <iostream>
#include <vector>
#include <cmath>
// ...(前面的代码保持不变,包括Matrix和Vector类型定义等)
boolluDecomposition(const Matrix& A, Matrix& L, Matrix& U){
size_t n = A.size();
L =Matrix(n,Vector(n,0.0));
U =Matrix(n,Vector(n,0.0));
for(size_t i =0; i < n;++i){
// 计算上三角矩阵 U
for(size_t k = i; k < n;++k){
double sum =0.0;
for(size_t j =0; j < i;++j){
sum += L[i][j]* U[j][k];
}
U[i][k]= A[i][k]- sum;
}
// 计算下三角矩阵 L
for(size_t k = i; k < n;++k){
if(i == k){
L[i][i]=1.0;// 对角线元素
}else{
double sum =0.0;
for(size_t j =0; j < i;++j){
sum += L[k][j]* U[j][i];
}
if(U[i][i]==0){
// 主元为零,无法进行LU分解
returnfalse;
}
L[k][i]=(A[k][i]- sum)/ U[i][i];
}
}
}
returntrue;
}
intmain(){
// 示例矩阵A
Matrix A ={
{2,3,1},
{4,7,7},
{6,18,22}
};
Matrix L, U;
// 进行LU分解
if(luDecomposition(A, L, U)){
std::cout <<"下三角矩阵L:"<< std::endl;
printMatrix(L);
std::cout <<"\n上三角矩阵U:"<< std::endl;
printMatrix(U);
// 验证A = LU
Matrix LU =multiplyMatrix(L, U);
std::cout <<"\n验证A = LU:"<< std::endl;
printMatrix(LU);
}else{
std::cout <<"无法进行LU分解。"<< std::endl;
}
return0;
}运行结果:
下三角矩阵L:
1 0 0
2 1 0
3 3 1
上三角矩阵U:
2 3 1
0 1 5
0 0 3
验证A = LU:
2 3 1
4 7 7
6 18 224.11 下三角 - 对角 - 上三角(LDU)分解
下三角 - 对角 - 上三角(LDU)分解是一种将矩阵表示为下三角矩阵、对角矩阵和上三角矩阵乘积的方法:
A=LDU
其中:
- L
是一个单位下三角矩阵(对角线元素全为1,下三角元素可能非零)。
- D
是一个对角矩阵(只有对角线元素非零)。
- U
是一个单位上三角矩阵(对角线元素全为1,上三角元素可能非零)。
LDU分解的步骤:
- 进行LU分解:
首先将矩阵A进行LU分解,得到A=LU
,其中L为下三角矩阵,U为上三角矩阵。 - 分离对角矩阵:
将L和U的对角线元素分离出来,组成对角矩阵D。
- 规范化L和U:
将L和U的对角线元素归一化为1,得到单位三角矩阵。
实现代码(C++语言):
#include <iostream>
#include <vector>
#include <cmath>
typedef std::vector<double> Vector;
typedef std::vector<Vector> Matrix;
// LU分解函数(用于LDU分解的基础)
boolluDecomposition(const Matrix& A, Matrix& L, Matrix& U){
size_t n = A.size();
L =Matrix(n,Vector(n,0.0));
U =Matrix(n,Vector(n,0.0));
for(size_t i =0; i < n;++i){
// 计算U的第i行
for(size_t k = i; k < n;++k){
double sum =0.0;
for(size_t j =0; j < i;++j)
sum += L[i][j]* U[j][k];
U[i][k]= A[i][k]- sum;
}
// 计算L的第i列
for(size_t k = i; k < n;++k){
if(i == k)
L[i][i]=1.0;// 对角线元素设为1
else{
double sum =0.0;
for(size_t j =0; j < i;++j)
sum += L[k][j]* U[j][i];
if(U[i][i]==0.0){
// 主元为零,无法继续
returnfalse;
}
L[k][i]=(A[k][i]- sum)/ U[i][i];
}
}
}
returntrue;
}
// LDU分解函数
boollduDecomposition(const Matrix& A, Matrix& L, Matrix& D, Matrix& U){
size_t n = A.size();
Matrix LU_L, LU_U;
// 进行LU分解
if(!luDecomposition(A, LU_L, LU_U)){
returnfalse;
}
// 初始化D为零矩阵
D =Matrix(n,Vector(n,0.0));
// 将LU分解的对角线元素分离到D矩阵中,并规范化L和U
L =Matrix(n,Vector(n,0.0));
U =Matrix(n,Vector(n,0.0));
for(size_t i =0; i < n;++i){
// 提取D的对角线元素
D[i][i]= LU_U[i][i];
// 规范化U矩阵的第i行
for(size_t j = i; j < n;++j){
if(D[i][i]==0.0){
// 对角线元素为零,无法规范化
returnfalse;
}
U[i][j]= LU_U[i][j]/ D[i][i];
}
// 将L矩阵的第i列复制过来(对角线元素为1)
for(size_t j =0; j <= i;++j){
L[i][j]= LU_L[i][j];
}
}
returntrue;
}
// 打印矩阵
voidprintMatrix(const Matrix& M){
for(constauto& row : M){
for(double val : row){
std::cout << val <<"\t";
}
std::cout <<"\n";
}
}
intmain(){
// 示例矩阵A
Matrix A ={
{4,2,0},
{4,4,2},
{2,2,3}
};
Matrix L, D, U;
if(lduDecomposition(A, L, D, U)){
std::cout <<"矩阵L(单位下三角矩阵):\n";
printMatrix(L);
std::cout <<"\n矩阵D(对角矩阵):\n";
printMatrix(D);
std::cout <<"\n矩阵U(单位上三角矩阵):\n";
printMatrix(U);
// 验证A = LDU
// 计算L * D
Matrix LD(L.size(),Vector(D[0].size(),0.0));
for(size_t i =0; i < L.size();++i)
for(size_t j =0; j < D[0].size();++j)
for(size_t k =0; k < D.size();++k)
LD[i][j]+= L[i][k]* D[k][j];
// 计算(LD) * U
Matrix LDU(LD.size(),Vector(U[0].size(),0.0));
for(size_t i =0; i < LD.size();++i)
for(size_t j =0; j < U[0].size();++j)
for(size_t k =0; k < U.size();++k)
LDU[i][j]+= LD[i][k]* U[k][j];
std::cout <<"\n验证A = LDU:\n";
printMatrix(LDU);
}else{
std::cout <<"无法对矩阵进行LDU分解。\n";
}
return0;
}代码详解:
LU分解函数
luDecomposition:该函数执行标准的LU分解,将矩阵A分解为L和U。
- L
是下三角矩阵,U 是上三角矩阵。
LDU分解函数
lduDecomposition:利用L分解的结果,将对角线元素提取到D中。
将L和U规范化为单位三角矩阵(即对角线元素为1)。
对于U,将其每一行除以对应的D的对角线元素。
主函数
main:定义一个示例矩阵A。
调用
lduDecomposition函数进行LDU分解。输出L、D、U矩阵,并验证A=LDU 。
运行结果:
矩阵L(单位下三角矩阵):
1 0 0
1 1 0
0.5 0 1
矩阵D(对角矩阵):
4 0 0
0 2 0
0 0 2
矩阵U(单位上三角矩阵):
1 0.5 0
0 1 1
0 0 1
验证A = LDU:
4 2 0
4 4 2
2 2 34.12 特征值和特征向量
特征值和特征向量是线性代数中的重要概念。对于线性变换TT,如果存在一个非零向量vv和标量λλ,使得:

4.13 特征值和特征向量的计算
为了计算矩阵AA的特征值λλ和对应的特征向量vv,我们需要解以下方程:

4.13.1 计算特征值和特征向量的示例
示例矩阵:

实现代码(C++语言,使用Eigen库):
#include <iostream>
#include <Eigen/Dense>
intmain(){
// 定义矩阵A
Eigen::Matrix3d A;
A <<2,0,0,
0,4,5,
0,4,3;
// 计算特征值和特征向量
Eigen::EigenSolver<Eigen::Matrix3d>es(A);
// 输出特征值
std::cout <<"特征值:"<< std::endl << es.eigenvalues()<< std::endl;
// 输出特征向量
std::cout <<"\n特征向量:"<< std::endl << es.eigenvectors()<< std::endl;
return0;
}代码详解:
使用Eigen库的
EigenSolver类可以方便地计算矩阵的特征值和特征向量。eigenvalues()返回特征值的复数类型,即使特征值是实数。
eigenvectors()返回特征向量,每一列对应一个特征向量。
运行结果:
特征值:
(-1,0)
(2,0)
(8,0)
特征向量:
(0,0) (1,0) (0,0)
(0.83205,0) (0,0) (0.5547,0)
(-0.5547,0) (0,0) (0.83205,0)4.14 矩阵的特征分解
特征分解(也称为谱分解)是将一个矩阵分解为其特征值和特征向量的方式。对n×n
的矩阵A,如果A有n个线性无关的特征向量,则A可以分解为:

4.15 奇异值分解(SVD)
奇异值分解(SVD)是将任意矩阵(实或复)分解为三个矩阵的乘积:



实现代码(C++语言,使用Eigen库):
#include <iostream>
#include <Eigen/Dense>
intmain(){
// 定义矩阵M
Eigen::MatrixXd M(3,2);
M <<1,0,
0,1,
1,1;
// 进行奇异值分解
Eigen::JacobiSVD<Eigen::MatrixXd>svd(M, Eigen::ComputeFullU | Eigen::ComputeFullV);
// 输出U矩阵
std::cout <<"矩阵U:"<< std::endl << svd.matrixU()<< std::endl;
// 输出奇异值
std::cout <<"\n奇异值:"<< std::endl << svd.singularValues()<< std::endl;
// 输出V矩阵
std::cout <<"\n矩阵V:"<< std::endl << svd.matrixV()<< std::endl;
// 验证M = U * Σ * V^T
Eigen::MatrixXd Sigma = Eigen::MatrixXd::Zero(3,2);
Sigma.diagonal()= svd.singularValues();
Eigen::MatrixXd M_reconstructed = svd.matrixU()* Sigma * svd.matrixV().transpose();
std::cout <<"\n重构的矩阵M:"<< std::endl << M_reconstructed << std::endl;
return0;
}代码详解:
使用
Eigen::JacobiSVD类进行奇异值分解。ComputeFullU和
ComputeFullV标志用于计算完整的UU和VV矩阵。奇异值存储在
singularValues()中,是一个向量。重构原矩阵用于验证SVD的正确性。
运行结果:
矩阵U:
-0.408248 0.816497 -0.408248
-0.408248 -0.57735 -0.707107
-0.816497 0 0.57735
奇异值:
1.73205
1
0
矩阵V:
-0.707107 -0.707107
-0.707107 0.707107
重构的矩阵M:
1 2.46e-16
1.95e-16 1
1 14.15.1 奇异值分解的应用
4.15.1.1 伪逆

应用:
- 求解线性方程组的最小二乘解。
- 处理欠定或超定方程组。
实现代码(C++语言,使用Eigen库):
#include <iostream>
#include <Eigen/Dense>
intmain(){
// 定义矩阵M
Eigen::MatrixXd M(2,3);
M <<1,2,3,
4,5,6;
// 定义向量b
Eigen::VectorXd b(2);
b <<7,8;
// 使用SVD计算M的伪逆
Eigen::JacobiSVD<Eigen::MatrixXd>svd(M, Eigen::ComputeThinU | Eigen::ComputeThinV);
Eigen::VectorXd x = svd.solve(b);
// 输出最小二乘解
std::cout <<"最小二乘解x:"<< std::endl << x << std::endl;
return0;
}代码详解:

运行结果:
最小二乘解x:
-3.05556
0.111111
3.277784.15.1.2 求解齐次线性方程组

实现代码(C++语言,使用Eigen库):
#include <iostream>
#include <Eigen/Dense>
intmain(){
// 定义矩阵A
Eigen::MatrixXd A(2,3);
A <<1,2,-1,
2,4,-2;
// 进行SVD分解
Eigen::JacobiSVD<Eigen::MatrixXd>svd(A, Eigen::ComputeFullV);
// 获取奇异值
Eigen::VectorXd singular_values = svd.singularValues();
// 获取V矩阵
Eigen::MatrixXd V = svd.matrixV();
// 寻找零空间的基
double tol =1e-10;
int n = V.cols();
int r = svd.rank();
std::cout <<"矩阵A的秩:"<< r << std::endl;
std::cout <<"\nA的零空间基向量:"<< std::endl;
for(int i = r; i < n;++i){
std::cout << V.col(i)<< std::endl <<"---"<< std::endl;
}
return0;
}代码详解:
- 计算矩阵的秩:
通过奇异值大于容差
tol的数量确定矩阵的秩。 - 提取零空间基向量:
V矩阵中对应于零奇异值的列向量。
- 容差
tol的选择:根据数值精度适当选择。
运行结果:
矩阵A的秩:1
A的零空间基向量:
0.408248
-0.816497
0.408248
---4.15.1.3 值域、零空间和秩
- 值域(列空间):
由A的左奇异向量(对应于非零奇异值)生成的空间。
- 零空间:
由A的右奇异向量(对应于零奇异值)生成的空间。
- 矩阵的秩:
非零奇异值的数量。
实现代码:
(与前一节类似,不再重复)
4.15.1.4 最近的正交矩阵
在许多应用中,需要找到与给定矩阵最接近的正交矩阵。对于矩阵AA,最近的正交矩阵OO可以通过SVD求解:

实现代码(C++语言,使用Eigen库):
#include <iostream>
#include <Eigen/Dense>
intmain(){
// 定义矩阵A
Eigen::MatrixXd A(3,3);
A <<1,2,3,
0,1,4,
5,6,0;
// 进行SVD分解
Eigen::JacobiSVD<Eigen::MatrixXd>svd(A, Eigen::ComputeFullU | Eigen::ComputeFullV);
// 计算最近的正交矩阵O
Eigen::MatrixXd O = svd.matrixU()* svd.matrixV().transpose();
// 输出结果
std::cout <<"最近的正交矩阵O:"<< std::endl << O << std::endl;
// 验证O是否为正交矩阵:O^T * O = I
Eigen::MatrixXd I = O.transpose()* O;
std::cout <<"\n验证O是否为正交矩阵(O^T * O):"<< std::endl << I << std::endl;
return0;
}代码详解:

运行结果:
最近的正交矩阵O:
-0.27524 0.79073 -0.54612
-0.47995 0.38454 0.78897
-0.83205 -0.47673 -0.28335
验证O是否为正交矩阵(O^T * O):
1 0 -5.55112e-17
0 1 -1.11022e-16
-5.55112e-17 -1.11022e-16 15. 线性映射

6. 张成空间

7. 子空间

8. 矩阵的值域(列空间)
矩阵的值域(Range),也称为矩阵的列空间,是由矩阵的列向量线性组合构成的向量空间。
计算矩阵的列空间:
要找到矩阵 AA 的列空间的基,可以执行以下步骤:
将矩阵 AA 化为列简化阶梯形(Column Echelon Form)。
确定主元列: 主元所在的列对应于列空间的基向量。
提取基向量: 从原矩阵 AA 中提取对应于主元列的列向量。
使用Eigen库计算列空间的基:
#include <iostream>
#include <Eigen/Dense>
// 定义模板函数,计算矩阵的列空间基
template<typenameT>
Eigen::Matrix<T, Eigen::Dynamic, Eigen::Dynamic>
ComputeColumnSpaceBasis(const Eigen::Matrix<T, Eigen::Dynamic, Eigen::Dynamic>&M){
// 使用CompleteOrthogonalDecomposition来计算完全正交分解
Eigen::CompleteOrthogonalDecomposition<Eigen::Matrix<T, Eigen::Dynamic, Eigen::Dynamic>>cod(M);
// 获取Q矩阵
const Eigen::Matrix<T, Eigen::Dynamic, Eigen::Dynamic> Q = cod.householderQ();
// 提取前rank列,作为列空间的基
return Q.leftCols(cod.rank());
}
intmain(){
// 示例矩阵
Eigen::MatrixXd M(4,5);
M <<2,4,1,3,2,
-1,-2,1,0,5,
1,6,2,2,2,
3,6,2,5,1;
// 计算列空间基
Eigen::MatrixXd basis =ComputeColumnSpaceBasis(M);
// 输出列空间的基向量
std::cout <<"矩阵的列空间基为:"<< std::endl << basis << std::endl;
return0;
}代码详解:
模板函数
ComputeColumnSpaceBasis:输入:矩阵
M。使用
Eigen::CompleteOrthogonalDecomposition类对矩阵进行完全正交分解。获取正交矩阵
Q,然后根据矩阵的秩(cod.rank())提取前rank列,作为列空间的基向量。
主函数
main:定义示例矩阵
M。调用
ComputeColumnSpaceBasis函数计算列空间的基。输出基向量。
运行结果:
矩阵的列空间基为:
-0.42881 -0.594356 0.0933123 0.673027
0.0797832 -0.379739 -0.830404 -0.401093
-0.275241 -0.647357 0.197248 -0.68951
-0.852604 0.279241 0.513828 -0.08825888.1 行空间示例
考虑矩阵:

9. 基
基是在向量空间中,能够唯一表示空间中任一向量的一组线性无关向量。基向量的数量等于向量空间的维数。
找到矩阵的列空间或行空间的基:
列空间的基:
将矩阵化为行简化阶梯形。
选取主元列所在的列向量作为基向量。
行空间的基:
将矩阵化为行简化阶梯形。
选取所有非零行作为基向量。
9.1 计算列空间基的示例

9.2 计算行空间基的示例
示例矩阵:

9.3 基向量的变换
在向量空间中,我们常常需要在不同的基之间进行转换。假设我们有两组基:

9.4 向量的协变与逆变
在基变换过程中,向量的表示(坐标)和基向量本身可能会以相反的方式变化,这涉及到协变和逆变的概念。
逆变(Contravariant)分量:
如果基向量放大(如长度加倍),那么向量的坐标会缩小(减半),以保持向量自身不变。
协变(Covariant)分量:
基向量放大,向量的坐标也相应放大。

9.5 创建一个基集
创建一个基集的目的是找到一组线性无关的向量,这些向量的线性组合可以覆盖整个向量空间。
从给定向量集合中挑选:
检查向量集合的线性相关性。
使用高斯消元法或行简化阶梯形来确定线性无关的向量。
9.6 基变换
基变换(Change of Basis)涉及从一种基到另一种基的转换,使得向量和线性映射在新的基下有不同的表示形式。

示例:
(与 9.3 相同的基变换过程。)
9.7 向量场
向量场是在空间中的每一点分配一个向量的函数,用于描述各种物理现象,例如速度场、电场和引力场。

9.8 坐标系
坐标系是在空间中确定点的位置的体系。常见的坐标系包括:
9.8.1 笛卡尔坐标、极坐标、柱坐标和球坐标

9.9 坐标变换
坐标变换是从一种坐标系到另一种坐标系的转换,主要用于简化问题或适应特定对称性。
9.10 仿射变换与曲线变换
仿射变换是保持点、直线和平面间的平行关系的变换,包括平移、旋转、缩放和剪切。

曲线坐标变换涉及到非线性坐标系的转换,例如从笛卡尔坐标到极坐标
10. 矩阵的秩

10.1 关于计算秩的结论
在实际计算中,由于计算机上的浮点误差,直接使用高斯消元法(LU 分解)可能不可靠。因此,应该使用能够揭示秩的分解方法,如 带主元选取的 QR 分解(揭示秩的 QR 分解,Rank-Revealing QR Decomposition)。奇异值分解(SVD) 也可以用来计算矩阵的秩,但对于大矩阵而言效率可能较低。
使用 Eigen 库计算矩阵的秩:
#include <iostream>
#include <Eigen/Dense>
intmain(){
// 定义矩阵A
Eigen::MatrixXd A(3,4);
A <<1,2,3,4,
2,4,6,8,
3,6,9,12;
// 使用FullPivLU分解来计算秩
Eigen::FullPivLU<Eigen::MatrixXd>lu_decomp(A);
int rank = lu_decomp.rank();
// 输出矩阵的秩
std::cout <<"矩阵A的秩为:"<< rank << std::endl;
return0;
}代码详解:
Eigen::FullPivLU类:该类可以使用完全主元选取的 LU 分解来计算矩阵的秩、零空间等。
lu_decomp.rank():获取矩阵的秩。
运行结果:
矩阵A的秩为:1解释:
矩阵 AA 的行是线性相关的,因此其秩为 1。
11. 列空间的维数
矩阵的列空间(也称为值域)的维数称为矩阵的秩。它表示矩阵的列向量中线性无关的最大数量。

12. 零空间(核)

12.1 计算零空间的示例
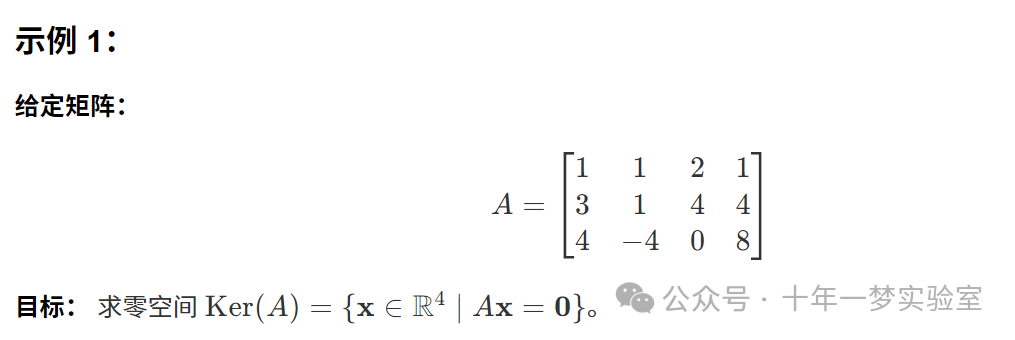

使用 Eigen 库计算零空间:
#include <iostream>
#include <Eigen/Dense>
intmain(){
// 定义矩阵A
Eigen::MatrixXd A(3,4);
A <<1,1,2,1,
3,1,4,4,
4,-4,0,8;
// 使用FullPivLU分解计算零空间
Eigen::FullPivLU<Eigen::MatrixXd>lu_decomp(A);
Eigen::MatrixXd null_space = lu_decomp.kernel();
// 输出零空间的基
std::cout <<"零空间的基向量为:"<< std::endl << null_space << std::endl;
return0;
}代码详解:
Eigen::FullPivLU类:可以计算矩阵的零空间。
lu_decomp.kernel():返回一个矩阵,其列为零空间的基向量。
运行结果:
零空间的基向量为:
-3 -4
1 0
0 1
2 2验证 Ax=0
:
// 验证 Ax = 0
Eigen::MatrixXd zeros = A * null_space;
std::cout << "验证 A * x = 0:" << std::endl << zeros << std::endl;结果:
验证 A * x = 0:
0 0
0 0
0 013. 零度

参考文献:
[1] https://math.stackexchange.com/questions/1375305/finding-the-null-space-of-a-matrix
[2] https://eigen.tuxfamily.org/dox/group__TutorialAdvancedLinearAlgebra.html
[3] https://www.math.purdue.edu/~sellke/linearalgebra/index6.html
14. 秩 - 零度定理
秩 - 零度定理是线性代数中的一个重要定理,它揭示了线性变换的秩(Rank)和零度(Nullity)之间的关系。

15. 矩阵的行列式
行列式(Determinant 是方阵的一个标量值,具有重要的代数和几何意义。

15.1 矩阵行列式的解释
1. 几何解释:
- 面积或体积的缩放因子:
在二维空间中,矩阵的行列式表示线性变换对面积的缩放因子;在三维空间中,表示对体积的缩放因子。
- 方向性:
行列式的符号表示线性变换是否保留了空间的定向。正的行列式表示保持定向,负的表示改变定向。
2. 代数解释:

数值示例:
示例 1:零行列式

使用 C++ 和 Eigen 库计算行列式:
#include <iostream>
#include <Eigen/Dense>
intmain(){
// 示例 1
Eigen::Matrix2d A;
A <<1,2,
2,4;
double detA = A.determinant();
std::cout <<"矩阵 A 的行列式为:"<< detA << std::endl;
// 示例 2
Eigen::Matrix2d B;
B <<3,0,
0,2;
double detB = B.determinant();
std::cout <<"矩阵 B 的行列式为:"<< detB << std::endl;
return0;
}代码详解:
Matrix2d:表示 2×22×2 的矩阵类型。
.determinant():计算矩阵的行列式。
运行结果:
矩阵 A 的行列式为:0
矩阵 B 的行列式为:616. 求矩阵的逆

使用 C++ 和 Eigen 库求逆矩阵:
#include <iostream>
#include <Eigen/Dense>
intmain(){
// 定义一个可逆矩阵 A
Eigen::Matrix3d A;
A <<4,7,2,
3,5,1,
2,4,1;
// 检查行列式是否非零
double detA = A.determinant();
if(detA ==0){
std::cout <<"矩阵不可逆,行列式为零。"<< std::endl;
return0;
}
// 计算逆矩阵
Eigen::Matrix3d A_inv = A.inverse();
// 输出逆矩阵
std::cout <<"矩阵 A 的逆矩阵为:"<< std::endl << A_inv << std::endl;
// 验证 A * A_inv = I
Eigen::Matrix3d I = A * A_inv;
std::cout <<"\n验证 A * A_inv = I:"<< std::endl << I << std::endl;
return0;
}代码详解:
.inverse():计算矩阵的逆矩阵。
- 先检查行列式:
如果行列式为零,矩阵不可逆,避免计算错误。
运行结果:
矩阵 A 的逆矩阵为:
5 -14 7
-2 6 -3
-1 2 -1
验证 A * A_inv = I:
1 0 0
0 1 0
0 0 1解释:

17. 线性代数基本定理
基本定理:
线性代数的四个基本子空间:

18. 置换矩阵
置换矩阵(Permutation Matrix 是一个方阵,通过交换单位矩阵的行或列得到。
定义:
置换矩阵的每一行和每一列都恰有一个元素为 1,其余元素为 0。
置换矩阵用于描述行或列的交换操作。
示例:
交换矩阵的第 2 行和第 3 行,得到一个 4×4
的置换矩阵:

使用 C++ 和 Eigen 库创建置换矩阵:
#include <iostream>
#include <Eigen/Dense>
intmain(){
// 创建 4x4 单位矩阵
Eigen::Matrix4d I = Eigen::Matrix4d::Identity();
// 创建置换矩阵,交换第 2 行和第 3 行
Eigen::PermutationMatrix<4> P;
// 定义置换向量
Eigen::Array4i indices;
indices <<0,2,1,3;// 表示新的行顺序
P.indices()= indices;
// 应用置换
Eigen::Matrix4d PermutationMatrix = P * I;
// 输出置换矩阵
std::cout <<"置换矩阵 P 为:"<< std::endl << PermutationMatrix << std::endl;
return0;
}代码详解:
PermutationMatrix:Eigen 提供的置换矩阵类型。
indices:定义置换矩阵的索引序列。
P * I:生成置换矩阵。
运行结果:
置换矩阵 P 为:
1 0 0 0
0 0 1 0
0 1 0 0
0 0 0 119. 增广矩阵
增广矩阵(Augmented Matrix 是将线性方程组的系数矩阵与其常数项向量合并而成的矩阵。
形式:

用途:
- 解线性方程组:
通过对增广矩阵进行行变换,可求解方程组的解。
- 判断解的情况:
增广矩阵的阶梯形形式可用于判断方程组是否有唯一解、无解或无穷多解。
使用 C++ 和 Eigen 库求解线性方程组:
#include <iostream>
#include <Eigen/Dense>
intmain(){
// 系数矩阵 A
Eigen::MatrixXd A(3,3);
A <<2,-1,1,
3,2,-4,
-6,3,-3;
// 常数项向量 b
Eigen::VectorXd b(3);
b <<1,4,2;
// 将 A 和 b 组合成增广矩阵
Eigen::MatrixXd AugmentedMatrix(A.rows(), A.cols()+1);
AugmentedMatrix << A, b;
// 输出增广矩阵
std::cout <<"增广矩阵 [A | b] 为:"<< std::endl << AugmentedMatrix << std::endl;
// 检查矩阵是否可逆
if(A.determinant()==0){
std::cout <<"系数矩阵 A 不可逆,可能无唯一解。"<< std::endl;
}else{
// 直接求解 Ax = b
Eigen::VectorXd x = A.colPivHouseholderQr().solve(b);
std::cout <<"\n方程组的解为:"<< std::endl << x << std::endl;
}
return0;
}代码详解:
- 构建增广矩阵:
将 A 和 b 合并。
.colPivHouseholderQr().solve(b):使用 QR 分解求解线性方程组。
- 检查行列式:
判断系数矩阵是否可逆。
运行结果:
增广矩阵 [A | b] 为:
2 -1 1 1
3 2 -4 4
-6 3 -3 2
方程组的解为:
0.5
1
2总结:
通过上述内容,我们进一步深入了解了线性代数中的一些核心概念:
秩 - 零度定理揭示了线性变换的秩和零度与起始空间维数的关系。
矩阵的行列式具有重要的几何和代数意义,用于判断矩阵的可逆性和线性变换的性质。
求矩阵的逆和解线性方程组是线性代数的重要应用,增广矩阵和置换矩阵在计算过程中起到关键作用。
线性代数的基本定理和四个基本子空间是理解线性映射和矩阵结构的基础。




















 4429
4429

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








