本题解将证明所有用到的结论。
首先题目让我们求出 M M M 条割线中两两相交的有多少组，那相交的割线太多了，所以我们反着来：找平行的割线有哪些。
这里用数学推导来解释：
我们假设已经有两条直线平行且交同一个圆于 A , B , C , D A,B,C,D A,B,C,D 四个点：
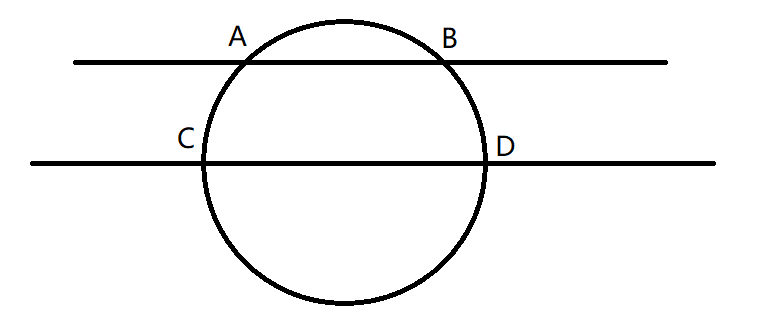
现在连接 A C , B D AC,BD AC,BD，于是我们得到了一个梯形：
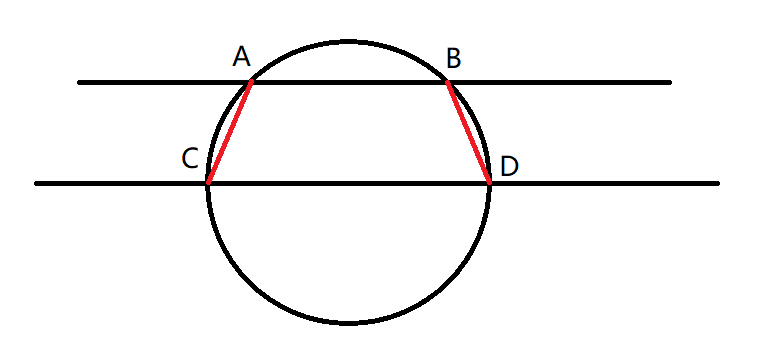
（辅助线用红线表示。）
那根据四点共圆的性质可知： ∠ C A B + ∠ C D B = 180 ∘ \angle CAB+\angle CDB=180^\circ ∠CAB+∠CDB=180∘。
又根据梯形的性质可知： ∠ A B D + ∠ C D B = 180 ∘ \angle ABD+\angle CDB=180^\circ ∠ABD+∠CDB=180∘。
所以可以得到： ∠ A B D = ∠ C A B \angle ABD=\angle CAB ∠ABD=∠CAB。
因此我们可以得到梯形 A B D C ABDC ABDC 是一个等腰梯形。
所以 A C = B D AC=BD AC=BD。
因为弦等，所以 A C ⏠ = B D ⏠ \overgroup{AC}=\overgroup{BD} AC =BD 。
那么我们记 A A A 为 i i i， B B
最低0.47元/天 解锁文章
扫一扫
1045
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
