目录
1.AES 加密算法原理
AES是一个迭代的、对称密钥分组的密码,它可以使用128、192和256位密钥,并且用128位(16字节)分组加密和解密数据。与公共密钥密码使用密钥对不同,对称密钥密码使用相同的密钥加密和解密数据。通过分组密码返回的加密数据的位数与输入数据相同。迭代加密使用一个循环结构,在该循环中重复置换(permutations)和替换(substitutions)输入数据。
一个密码算法的有效性首先体现在可靠的安全性上。Rijndael算法设计采用针对差分和线性密码分析提出的宽轨迹策略(WTS),其最大优势是可以给出算法最佳差分特征的概率以及最佳线性逼近偏差的界;使用简单的部件组织成清晰的结构,便于算法安全性的分析。当然,在密码学界永远没有绝对的安全,Rijndael算法也不例外,如其明显的代数结构对安全性的潜在威胁已经受到一些学者的质疑。本文从简化算法攻击、算法结构性质分析以及密码分析的进展等方面对AES算法的密码分析状况进行讨论。
1.1 密钥
密钥(Key)是密码算法中参与运算的数值(或者数值集)。对报文进行加密,我们需要一个加密算法、一个加密密钥以及明文,并由此产生密文。对报文进行解密,我们需要一个解密算法、一个解密密钥以及密文,并由此复原原始的明文。
1.2 加密变换
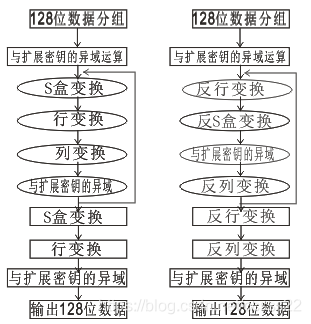
AES的加密和解密框图如图1所示。设X施AES的128比特明文输入,Y是128比特的密文输出,则AES的密文Y可以用下面的复合变换表示:Y=A k(r+1) R S Akr C R S A k(r1)…… C R S Ak1(X)
其中“”表示复合运算。这里Ak1 表示对X的一个变换Aki (X)=X ⊕KI(KI为第i轮的子密钥,为比特串的异或运算)。S:S盒置换。即对每一个字节用S-Box做一个置换。S-Box是一个给定的转换表。R:行置换。C:列置换。S’(x)=a(x)S(X)
1.3 S盒变换(Subyte)
对输入矩阵的任何一个元素A 做如下变换S[A]:

在行变换中,中间状态矩阵State的第一行不变;第二至四行做如下变换,即将表3的状态矩阵变为表四的状态矩阵。
在行变换中,中间状态矩阵State的第一行不变;第二至四行做如下变换,即将表3的状态矩阵变为表四的状态矩阵。

列变换是堆中间状态矩阵State逐列进行变换,其变换如下的矩阵运算:

经过上面的运算,原来的一列就被替换成下面的式子所表达的新列

这里的⊕为按位异或运算,其中的乘法X 按照下面介绍的模乘同余规则进行计算。
2.BPSK 调制解调原理
BPSK是一种简单的数字调制技术,它通过改变载波信号的相位来表示两个比特的状态(0和1)。具体来说,当输入比特为0时,载波相位保持不变;当输入比特为1时,载波相位翻转180度。假设输入的数据序列为b(n),其中b(n)∈{0,1}。载波信号可以表示为s(t)=Acos(2πfct+ϕ),其中 A 是幅度,fc 是载波频率,ϕ 是初始相位。


3.AES+BPSK加密通信系统
将待传输的明文数据按照 AES 加密算法进行加密,得到密文数据。对加密后的密文数据进行 BPSK 调制,将其转换为射频信号,并通过天线发送出去。
接收天线接收到信号后,进行 BPSK 解调,得到解调后的基带信号。对解调后的基带信号按照 AES 解密算法进行解密,恢复出原始的明文数据。
在实际应用中,还需要考虑信道编码、同步等问题,以提高系统的可靠性和性能。同时,对于 AES 加密算法的密钥管理和 BPSK 调制解调的参数优化也是关键因素,需要根据具体的应用场景和需求进行合理的设计和调整。
4.MATLAB程序
33...........................................
for ijk = 1:length(SNRs);
SNR=SNRs(ijk);
% 进行核心操作
% 使用扩展密钥、S 盒和多项式变换矩阵将明文转换为密文
% 调用 cipher 函数进行加密操作,将明文转换为密文
ciphertext = cipher (plaintext, w, s_box, poly_mat, 1);
%转换为二进制
tmps0=[];
for ij = 1:length(ciphertext)
tmps0 = [tmps0,double(dec2bin(ciphertext(ij),8))];
end
tmps0=tmps0-48;
for k = 1:1000
[k,ijk]
%BPSK
u = 2*tmps0-1;
%通过信道模型
ut= awgn(u,SNR);
%BPSK解调
U2 = round((sign(ut)+1)/2);
%转换回十进制
tmps=[];
for ij = 1:length(U2)/8
tt = U2(8*ij-7:8*ij);
tmps = [tmps,tt(1)*2^7+tt(2)*2^6+tt(3)*2^5+tt(4)*2^4+tt(5)*2^3+tt(6)*2^2+tt(7)*2^1+tt(8)*2^0];
end
ciphertextR=tmps;
% 将密文转换回明文
% 使用扩展密钥、逆 S 盒和逆多项式变换矩阵
% 调用 inv_cipher 函数进行解密操作,将密文还原为明文
re_plaintext = inv_cipher (ciphertextR, w, inv_s_box, inv_poly_mat, 1);
% 输出明文
plaintext;
% 输出密文
ciphertext;
% 输出还原后的明文
re_plaintext;
%计算错误个数
err(ijk,k) = 1-length(find(re_plaintext==plaintext))/length(plaintext);
end
if SNR==0
plaintext1=plaintext;
re_plaintext1=re_plaintext;
end
if SNR==4
plaintext2=plaintext;
re_plaintext2=re_plaintext;
end
if SNR==10
plaintext3=plaintext;
re_plaintext3=re_plaintext;
end
if SNR==20
plaintext4=plaintext;
re_plaintext4=re_plaintext;
end
end
figure;
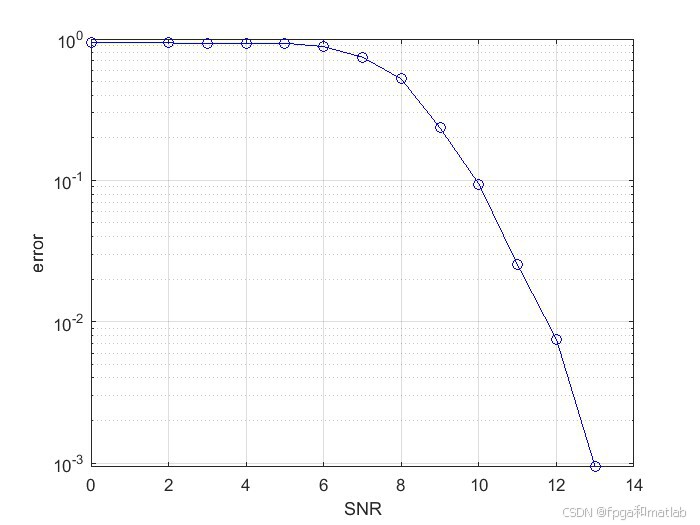
semilogy(SNRs,mean(err,2),'b-o');
xlabel('SNR');
ylabel('error');
grid on;
disp('输出明文');plaintext1
disp('SNR=0,输出AES还原后的明文');re_plaintext1
disp('SNR=4,输出AES还原后的明文');re_plaintext2
disp('SNR=10,输出AES还原后的明文');re_plaintext3
disp('SNR=20,输出AES还原后的明文');re_plaintext45.仿真结果
输出明文
plaintext1 =
0
17
34
51
68
85
102
119
136
153
170
187
204
221
238
255SNR=1,输出AES还原后的明文
re_plaintext1 =
182 244 109 144 210 226 138 155 108 13 120 17 8 81 6 116
SNR=5,输出AES还原后的明文
re_plaintext2 =
69 73 130 34 78 173 38 253 244 153 100 225 74 80 8 210
SNR=11,输出AES还原后的明文
re_plaintext3 =
0 17 34 51 68 85 102 119 136 153 170 187 204 221 238 255
SNR=20,输出AES还原后的明文
re_plaintext4 =
0 17 34 51 68 85 102 119 136 153 170 187 204 221 238 255
6.完整程序下载
完整可运行代码,博主已上传至优快云,使用版本为matlab2022a:

























 64
64

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










