目录
在现代监控系统中,摄像机的布置对于有效覆盖监控区域、提高监控质量至关重要。传统的摄像机布置方法通常基于经验或简单的几何规则,难以实现最优的布置方案。遗传算法(Genetic Algorithm,GA)作为一种强大的优化算法,能够在复杂的搜索空间中找到全局最优解,为摄像机最优布置问题提供了一种有效的解决方案。
1.摄像机最优布置问题描述
摄像机最优布置问题可以描述为:在给定的监控区域内,确定摄像机的位置和方向,使得摄像机能够最大限度地覆盖监控区域,同时满足一定的约束条件。
监控区域描述:监控区域可以用一个二维或三维空间来表示,通常由一系列的点、线、面或体组成。
摄像机模型:摄像机可以用一个数学模型来表示,通常包括位置、方向、视角、焦距等参数。
覆盖目标:摄像机的覆盖目标可以是监控区域内的点、线、面或体,也可以是特定的目标物体或区域。
约束条件:摄像机最优布置问题通常需要满足一些约束条件,例如摄像机的数量限制、安装位置限制、视角限制、成本限制等。
2.基于遗传算法的摄像机最优布置原理
编码方案
个体编码:将摄像机的位置和方向等参数编码为一个个体,通常可以采用实数编码或二进制编码等方式。例如,可以用一个三维向量表示摄像机的位置,用一个二维向量表示摄像机的方向。
种群编码:将一组个体编码为一个种群,通常可以采用数组或链表等数据结构来表示。
适应度函数设计
覆盖度评估:计算每个摄像机对监控区域的覆盖度,可以采用几何方法或模拟方法等方式。例如,可以计算摄像机的视角与监控区域的交集面积或体积,作为摄像机的覆盖度。
适应度函数定义:根据覆盖度评估结果,定义适应度函数,用于衡量个体对问题的适应程度。通常可以将适应度函数定义为覆盖度的函数,例如可以将适应度函数定义为覆盖度的总和或平均值。

遗传操作设计
选择操作:选择操作是遗传算法中的关键操作之一,它决定了哪些个体将被保留下来用于产生下一代个体。常用的选择操作有轮盘赌选择、锦标赛选择等方式。例如,可以采用轮盘赌选择方式,根据个体的适应度值计算每个个体被选中的概率,然后随机选择个体作为父代。

交叉操作:交叉操作是遗传算法中的另一个关键操作,它通过对父代个体进行交叉操作,产生新的子代个体。常用的交叉操作有单点交叉、两点交叉、均匀交叉等方式。例如,可以采用两点交叉方式,随机选择两个交叉点,将父代个体在交叉点之间的部分进行交换,产生新的子代个体。

变异操作:变异操作是遗传算法中的最后一个关键操作,它通过对子代个体进行变异操作,增加种群的多样性。常用的变异操作有随机变异、高斯变异等方式。例如,可以采用高斯变异方式,对子代个体的某些参数进行随机扰动,使其在一定范围内发生变化。

约束处理
约束条件检查:在遗传算法的每一代迭代中,需要对个体进行约束条件检查,确保个体满足问题的约束条件。如果个体不满足约束条件,可以采取一些措施进行处理,例如可以将不满足约束条件的个体替换为满足约束条件的个体,或者对不满足约束条件的个体进行修复操作。
3.MATLAB程序
......................................................................
ITER = [5,15,25,50];
for ij = 1:length(ITER)
%运行遗传算法
lb = zeros(1, nVar);
ub = ones(1, nVar);
intintices = (1:nVar);
initialx = zeros(1, nVar);
options = optimoptions(@ga, ...
'Display', 'iter', ...
'CrossoverFraction', 0.75, ...
'MaxStallGenerations', ITER(ij), ...
'PopulationSize', 500);
f = @(x) func_Coverage(x, Config, problem, cpara, b);
[x, fval] = ga(f, nVar, Aueq, bueq, [], [], lb, ub, @func_Constrains, intintices, options);
%% 绘制结果
figure;
% 场景初始化
axis off;
axis equal;
grid on;
set(gca, 'xtick', -10:2:120);
set(gca, 'ytick', -20:2:70);
% 轮廓
[n, ~] = size(ELC);
for i = 1:n
line([ELC(i, 1), ELC(i, 3)], [ELC(i, 2), ELC(i, 4)], 'LineWidth', 2, 'color', 'r');
end
hold on;
% 平面图和摄像机参数
for i = 1:numel(x)
if x(i) == 1
cpara.pos = Config(i, 1:3);
cpara.yaw = Config(i, 4);
cpara.pitch = Config(i, 5);
% 可视化多边形由许多采样点组成
PV_FOV = func_Polygon(EL, cpara);
fill(PV_FOV(:, 2), PV_FOV(:, 3), [0 0.9 0], 'FaceAlpha', 0.1);
hold on;
% 绘制视点以避免重叠
pos = cpara.pos;
plot(pos(1), pos(2), '.', 'Color', 'b', 'MarkerSize', 15);
hold on;
% 转换为UE4坐标
t = cpara.pos(1);
cpara.pos(1) = cpara.pos(2);
cpara.pos(2) = t;
cpara.pos = cpara.pos * 50;
cpara.yaw = -mod(cpara.yaw - 90, 360);
cpara.pitch = cpara.pitch - 90;
disp(cpara);
end
end
title(['GA优化迭代次数:',num2str(ITER(ij))]);
end4.仿真结果

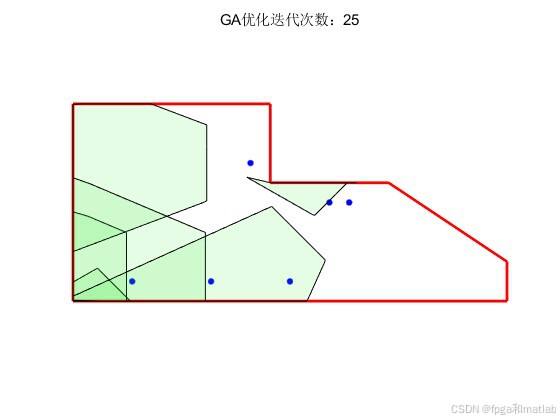
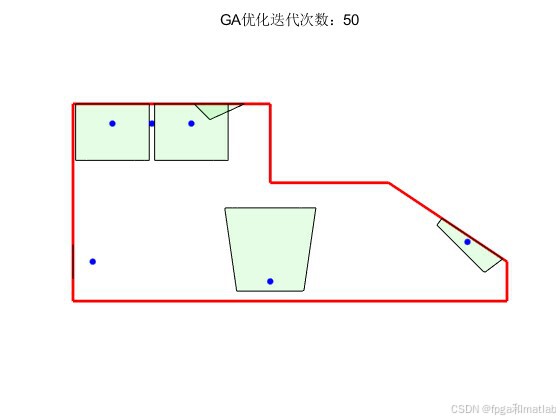

























 1万+
1万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










