基于OFDM和MMSE均衡的matlab误码率仿真

目录

1.正交频分复用（OFDM）

2.最小均方误差均衡器（MMSE）

3.MATLAB程序

4.仿真结果

---

1.正交频分复用（OFDM）

       OFDM是一种高效的多载波数字调制技术，其主要特点是将高速的数据流分解成多个较低速率的子数据流，每个子数据流在正交的子载波上进行调制传输。

       其中x[k]代表第k个子载波上的数据符号，X[n]是IFFT变换后的时域信号。接收端则执行相反的过程，即对收到的信号做FFT运算恢复子载波上的数据。

       循环前缀（Cyclic Prefix, CP） 为了对抗多径传播造成的符号间干扰（ISI），OFDM系统通常会在每个有效符号块之前添加一段循环前缀，其长度足以覆盖所有延迟传播导致的延时扩展。

实际应用中的挑战与解决方案

• 信道估计：在实际OFDM系统中，需要精确的信道状态信息来实现最佳解调和均衡。通常采用训练序列或导频信号进行信道估计。
• 峰均功率比（PAPR）问题：OFDM信号往往具有较高的峰值功率与平均功率之比，可能导致非线性失真。可以通过各种PAPR降低技术，如选择性映射（SLM）、剪切法、编码预失真等方法缓解这一问题。
• 同步问题：OFDM系统需要精确的时间和频率同步，包括符号定时同步、帧同步以及载波频率偏移校正。

       总之，OFDM技术通过高效的频谱利用率、良好的抗多径衰落性能以及易于实现的优点，广泛应用于现代无线通信标准中，如Wi-Fi (IEEE 802.11a/g/n/ac/ax), LTE, 5G NR等。

2.最小均方误差均衡器（MMSE）

       MMSE均衡器是一种线性预处理器，用于补偿无线信道中的频率选择性衰落和多径效应。在OFDM系统中，尽管IFFT和CP的设计有助于减少ISI，但在存在严重频率选择性衰落的情况下，仍需要均衡处理以提高接收性能。

       假设接收到的OFDM符号Y[n] 可表示为：

其中：

• H[n] 是频率响应矩阵，描述了从发射到接收各子载波的信道影响；
• X[n] 是发送的OFDM符号；
• W[n] 是加性高斯白噪声（AWGN）。

       MMSE均衡器的目标是在给定信道估计的基础上，找到一个线性滤波器 G[n]，使得均衡后输出X^[n] 最接近于原始发送符号X[n]，从而最小化均方误差（MSE）：

      通过求解这个优化问题，可以得到MMSE均衡器系数G[n]。对于单载波情况下的MMSE均衡器，表达式可以简化为：

其中H表示信道矩阵的共轭转置，σw2​ 是噪声功率，I 是单位矩阵。

       然而，在OFDM系统中，由于每个子载波独立地受到信道的影响，因此，每个子载波上的MMSE均衡实际上是针对该子载波的信道系数进行单独处理的。

       由于涉及实际应用中的OFDM-MMSE均衡会更加复杂，涉及到的是二维矩阵操作而非一维滤波器，且通常结合信道状态信息（CSI）估计以及子载波间的相关性等因素。因此，实际计算均衡器系数的过程会更为繁琐，需要考虑整个资源块内的信道矩阵及其逆运算或者近似算法。

3.MATLAB程序

function SER = ofdm(SP)

numSymbols = SP.FFTsize;
H_channel = fft(SP.channel,SP.FFTsize);

for n = 1:length(SP.SNR),
    tic;
    errCount = 0;

    for k = 1:SP.numRun,
        tmp = round(rand(2,numSymbols));
        tmp = tmp*2 - 1;
        inputSymbols = (tmp(1,:) + i*tmp(2,:))/sqrt(2);
        
        TxSamples = sqrt(SP.FFTsize)*ifft(inputSymbols);
    
        ofdmSymbol = [TxSamples(numSymbols-SP.CPsize+1:numSymbols) TxSamples];
        
        RxSamples = filter(SP.channel, 1, ofdmSymbol); % Multipath Channel
    
        tmp = randn(2, numSymbols+SP.CPsize);
        complexNoise = (tmp(1,:) + i*tmp(2,:))/sqrt(2);
        noisePower = 10^(-SP.SNR(n)/10);
        RxSamples = RxSamples + sqrt(noisePower)*complexNoise;
        
        EstSymbols = RxSamples(SP.CPsize+1:numSymbols+SP.CPsize);
        Y = fft(EstSymbols, SP.FFTsize);
        
        if SP.equalizerType == 'ZERO'
            Y = Y./H_channel;
        elseif SP.equalizerType == 'MMSE'
            C = conj(H_channel)./(conj(H_channel).*H_channel + 10^(-SP.SNR(n)/10));
            Y = Y.*C;
        end
        
        EstSymbols = Y;
        EstSymbols = sign(real(EstSymbols)) + i*sign(imag(EstSymbols));
        EstSymbols = EstSymbols/sqrt(2);

        I = find((inputSymbols-EstSymbols) == 0);
        errCount = errCount + (numSymbols-length(I));
    end
    SER(n,:) = errCount / (numSymbols*SP.numRun);
    [SP.SNR(n) SER(n,:)]
    toc
end
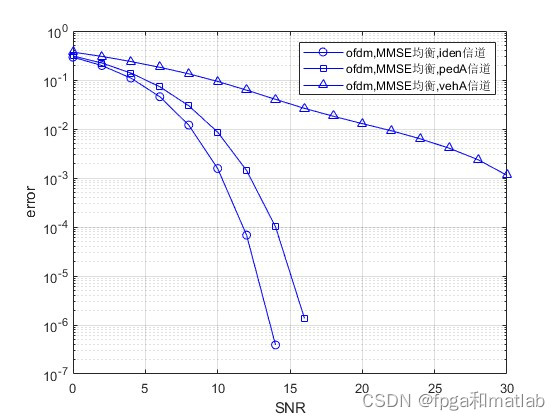
up4049

4.仿真结果