有限元方法仿真弹性体 (Finite Element Method, FEM)

Finite Element Method (FEM, 有限元方法) 时一种将物体看作许多有体积的微小单元来进行仿真的方法。比如将二维图形拆分成若干三角形，将三维体拆分成若干四面体。这种方法能够很好的模拟弹性体的形变等特点，能够在数学上证明其仿真方法一定收敛到解析解，比MPM等使用粒子模拟的方法更加准确，但同时也更加复杂，运算更慢。

本文将先从弹性体相关的物理量基础定义开始，再讲述各种弹性体的能量函数模型，最后阐述如何用有限元方法离散化进行仿真。

本文主要参考FEM simulation of 3D deformable solids Siggraph 2012 Course，并修正了一些不明确的可能错误的地方

弹性体基础

弹性体指的是能够自己恢复初始状态的材料

超弹性体（hyperelasticity）是一种特殊的弹性体，指的是弹力与压缩（拉伸）的路径没有关系，只与压缩后的状态有关系。

本文只考虑超弹性体。

形变与能量

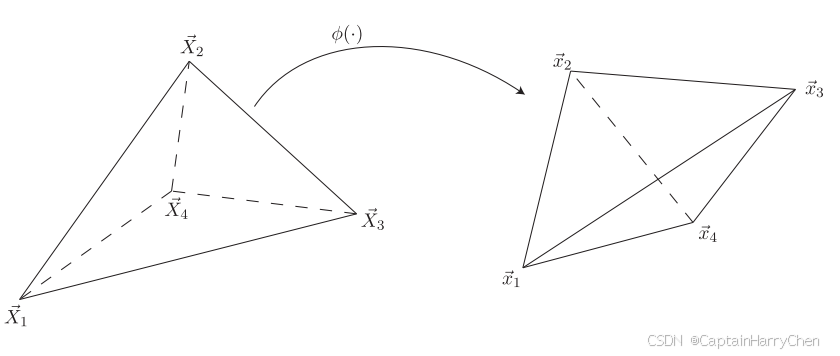
定义弹性体的区域为$\Omega$，弹性体上初始时每个点的位置为$X$。弹性体发生平移、形变等变化后，弹性体上每一个点都将移动到另一个位置$\text{x}$，可以用一个形变映射(deformation map)来表示弹性体的这一个变换$\text{x}=\varphi (X)$，如下图

$\varphi (X)$并不能表示形变，因为弹性体整体的移动不产生形变，而相近的点移动的区别产生形变，则可以使用形变映射函数到初始位置的导数作为表示形变的量：
$$F=\frac{\partial \varphi (X)}{\partial X}=\frac{\partial \text{x}}{\partial X}$$
在三维情况下，这是一个3×3的矩阵，即雅可比矩阵，$F$被称为形变梯度(deformation gradient)

$F$形变梯度表示某一点$X$相对其邻域的形变，形变产生弹性势能，所以需要定义针对这一点的能量密度$\Psi (\varphi ,X)$，弹性体的总能量即为$E(\varphi )={\int }_{\Omega }\Psi (\varphi ,X)\mathrm{d}X$. 一般情况下，能量密度只与形变梯度有关，可写为$\Phi (F)$.

注意到$\text{det}(F)=J=\frac{V_{变换后}}{V_{初始}}$，即$F$的行列式可以表示体积的变化

弹性内力

接下来计算弹性内力，在数学上需要区分内部力和边界力

对于体积内部，令$f(X)$表示位置$X$处的力密度(单位$N/m^3$)，则一个体积$A\subset \Omega$内的受力为${\text{f}}_{agg}(A)={\int }_{A}f(X)\mathrm{d}X$

对于边界上，令$\tau (X)$表示边界位置$X$处的力密度(单位$N/m^2$)，则一块三维体表面$B\subset \partial \Omega$的受力为${\text{f}}_{agg}(B)={\oint }_B\tau (X)\mathrm{d}X$

内力即为弹性势能梯度的相反方向，因为内力总是往使得势能减小最快的方向进行，所以内力可以为$\text{f}=-\frac{\partial E}{\partial \text{x}}$，注意这里是变换后的位置

PK1数

因为内力是势能的梯度相反方向，所以我们试图用总势能对位置求梯度，看看能得到什么
$$\begin{array}{rl}\delta E& =\delta \left[{\int }_{\Omega }\Psi (F)\mathrm{d}X\right]\\ & ={\int }_{\Omega }\delta \left[\Psi (F)\right]\mathrm{d}X\\ & ={\int }_{\Omega }\left[\frac{\partial \Psi }{\partial F}:\delta F\right]\mathrm{d}X\end{array}$$

注意公式中的$\left[A:B\right]$表示矩阵$A,B$按位点乘，上述公式是微分链式法则用到了点乘

之后$[:]$均表示按位点乘，有时候还需要按位点乘后再将每个元素加起来，请根据上下文判断

令$P=\frac{\partial \Psi }{\partial F}$，被称为PK1数(The first Piola-Kirchhoff stress tensor)，下面将推导$P$的几何意义

继续推导能量的微分：
$$\begin{array}{rl}\delta E& ={\int }_{\Omega }\left[P:\delta F\right]\mathrm{d}X\\ & ={\int }_{\Omega }\left[P:\frac{\partial }{\partial X}\delta \varphi (X)\right]\mathrm{d}X\end{array}$$

由高维分步积分拆开可以得到：

$$\begin{array}{rl}\delta E& =-{\int }_{\Omega }\text{div}P\cdot \delta \text{x}\cdot \mathrm{d}X+{\oint }_{\Omega }P\cdot \delta \text{x}\cdot \mathrm{d}S\\ & =-{\int }_{\Omega }\text{div}P\cdot \delta \text{x}\cdot \mathrm{d}X+{\oint }_{\Omega }(P\cdot N)\cdot \delta \text{x}\cdot \mathrm{d}X\end{array}$$
因为出现了对于当前位置$\text{x}$的微分$\delta \text{x}$，根据力的定义，可以把积分前半部分视为力密度

即$f(\text{x})=\text{div}P$，$\tau (\text{x})=-P\cdot N$

可以理解为PK1数表示的是对该点某一方向微平面的压强

弹性能量模型

本节将探讨不同的弹性模型如何从形变梯度定义能量密度，计算出内力

应变量度

为了计算出能量，我们需要一个衡量形变程度的度量方式，$F$只是一个表示形变的量，并不能衡量形变程度。

注意到形变梯度$F$实际上仅包含变换的旋转和拉伸，矩阵一定可以分解为$F=RS$，其中$R$为旋转矩阵，满足$R^{T}R=I$；$S$为拉伸矩阵，一定为对称的。形变的量度可以仅与拉伸有关：
$$E=\frac{1}{2}(S^2-I)=\frac{1}{2}(F^{T}F-I)$$
注意这里的$E$不是能量，这被称为格林应变张量(Green strain tensor)，是一个3×3的矩阵，用于衡量各个方向的形变程度。这是一个与旋转、平移无关的量度，但它是非线性的。

尝试简化，我们对$E$在$F=I$进行泰勒展开：
$$\begin{array}{rl}E(F)& \approx E(I)+\frac{\partial E}{\partial F}{|}_{F=I}:(F-I)\\ & =E(I)+\frac{1}{2}\left[(F-I{)}^{T}I+I^T(F-I)\right]\\ & =\frac{1}{2}(F+F^T)-I\end{array}$$
其中第一行到第二行的求法是使用微分$\frac{\partial E}{\partial F}:\delta F=\delta E=\frac{1}{2}(\delta F^{T}F+F^T\delta F)$

我们由此定义了另一个量度：
$$ϵ=\frac{1}{2}(F+F^T)-I$$
称为微小应变张量(small strain tensor, infinitesimal strain tensor)，是一个线性的应变张量，但其却是与旋转有关的，弹性体在不形变的情况下发生旋转也会改变$ϵ$

注意到$ϵ$一定为对称矩阵，其点乘一个反对称矩阵一定为$\text{0}$

线性弹性模型 Linear elasticity

定义：
$$\Psi (F)=\mu \text{tr}({ϵ}^2)+\frac{\lambda }{2}{\text{tr}}^2(ϵ)$$
这是线性弹性模型的能量密度，其中$\mu =\frac{k}{2(1+\nu )}$, $\lambda =\frac{k\nu }{(1+\nu )(1-2\nu )}$被称为拉梅系数 (Lamé coefficients) 。其中的$k$为杨氏模量 (Young’s modulus) ，一般表示拉伸抵抗性。$\nu$为泊松比，一般表示不可压缩性。

通过对$\Psi$微分来求$P$
$$\begin{array}{rl}\delta \Psi & =\mu \cdot \text{tr}(\delta ϵ\cdot ϵ+ϵ\delta ϵ)+\lambda \text{tr}(ϵ)\text{tr}(\delta ϵ)\\ \delta ϵ& =\frac{1}{2}\left(\delta F+\delta F^T\right)\doteq \text{Sym}(\delta F)\end{array}$$

注：任意矩阵都可以拆分为一个对称矩阵和反对称矩阵之和$A=\text{Sym}(A)+\text{Anti-Sym}(A)$

对称矩阵点乘一个矩阵：$ϵ:A=ϵ:\text{Sym}(A)$

注2：矩阵的迹中两矩阵相乘是可以交换的：$\text{tr}(AB)=\text{tr}(BA)$，可以展开对角线元素计算证明。还可以是可转置的$\text{tr}(A)=\text{tr}(A^T)$

注3：矩阵的迹的微分可以视为矩阵对角元素的微分，其余为0，则可以写为$\delta \text{tr}(ϵ)=\text{tr}(\delta ϵ)=I:\delta ϵ$

$$\begin{array}{rl}\delta \Psi & =2\mu \cdot \text{tr}(\delta ϵ\cdot ϵ)+\lambda \text{tr}(ϵ)\left(I:\text{Sym}(\delta F)\right)\\ & =2\mu \cdot (I:\text{Sym}(\delta F)ϵ)+\lambda \text{tr}(ϵ)\left(I:\text{Sym}(\delta F)\right)\\ & =2\mu \cdot (ϵ:\text{Sym}(\delta F{)}^T)+\lambda \text{tr}(ϵ)\left(I:\text{Sym}(\delta F)\right)\\ & =(2\mu ϵ+\lambda \text{tr}(ϵ)I):\text{Sym}(\delta F)\\ & =(2\mu ϵ+\lambda \text{tr}(ϵ)I):\delta F\\ \Rightarrow P& =2\mu ϵ+\lambda \text{tr}(ϵ)I\\ & =\mu (F+F^T-2I)+\lambda \text{tr}(F-I)I\end{array}$$

我们得出了线性弹性模型的PK1数：$P=\mu (F+F^T-2I)+\lambda \text{tr}(F-I)I$

这个模型是线性的，容易计算，但是其与旋转相关

圣维南-基尔霍夫模型 St. Venant-Kirchhoff model (STVK)

使用格林应变张量($E=\frac{1}{2}(F^{T}F-I)$)定义的非线性模型：(注意到$E$为对称矩阵)
$$\Psi (F)=\mu \text{tr}(E^2)+\frac{\lambda }{2}{\text{tr}}^2(E)$$
同样，对其微分来求 $P$：
$$\begin{array}{rl}\delta \Psi (F)& =2\mu \cdot \text{tr}(E\delta E)+\lambda \text{tr}(E)\text{tr}(\delta E)\\ \delta E& =\frac{1}{2}(\delta F^{T}F+F^T\delta F)=\text{Sym}(F^T\delta F)\\ \text{tr}(E\delta E)& =I:E\cdot \text{Sym}(F^T\delta F)=E:\text{Sym}(F^T\delta F{)}^T=E:F^T\delta F=FE:\delta F\\ \text{tr}(\delta E)& =I:\text{Sym}(F^T\delta F)=I:F^T\delta F=F:\delta F\\ \Rightarrow \delta \Psi (F)& =2\mu FE:\delta F+\lambda \text{tr}(E)F:\delta F\\ & =(2\mu FE+\lambda \text{tr}(E)F):\delta F\\ \Rightarrow P& =2\mu FE+\lambda \text{tr}(E)F=F(2\mu E+\lambda \text{tr}(E)I)\end{array}$$

注：上面第三行用了性质$A:B^{T}C=BA:C$，可以通过展开点乘和矩阵乘法证明

注2：点乘易错点$A(B:C)\ne (AB):C$

于是我们得到了StVK模型的PK1数：$P=F(2\mu E+\lambda \text{tr}(E)I)$

这其实是一个关于$F$的三次式，十分复杂，运算复杂度高，优势在于他是一个旋转无关的模型，更符合现实。其仍有仿真缺陷，当弹性体被压缩到一定程度后，其抵抗压缩的力会突然减小（？），导致弹性体更容易被压缩到一个质点

共旋转线性模型 (Corotated Linear Elasticity)

线性模型没有旋转无关性，StVK效率很低，于是Corotated Linear Elasticity试图折衷考虑两者。

比较复杂，不细讲
$$\Psi (F)=\mu \Vert S-I{\Vert }_F^2+\frac{\lambda }{2}{\text{tr}}^2(S-I)$$
其中$S$为包含在$F$中的拉伸矩阵$F=RS$
$$P=2\mu (F-R)+\lambda \text{tr}(R^{T}F-I)R$$
相比于线性模型，直观的理解是这个模型手动减去$R$直接去除旋转的影响

旋转无关、各向同性与NeoHookean模型

旋转无关，指弹性体整体旋转不会改变每个位置的能量密度，可以写为$\Psi (RF)=\Psi (F)$，即先变换后，再进行旋转不会影响能量。

各向同性，弹性体从任意方向进行相同的变换（拉伸旋转平移等）不会影响每个位置的能量密度，可以写为$\Psi (FQ)=\Psi (F)$，即先旋转再进行相同的变换不影响能量。

若模型既是旋转无关也是各向同性的，则能量密度函数满足：$\Psi (RFQ)=\Psi (F)$

根据这个形式，自然想到将$F$进行奇异值分解(SVD) ：$F=U\Sigma V^T$，其中$U$和$V$一定为酉矩阵，即$U^{T}U=V^{T}V=I$，与旋转矩阵一致。而$\Sigma$为对角矩阵，在3维情况下自由度仅为3.

故一个满足旋转无关且各向同性的模型，一定满足$\Psi (F)=\Psi (\Sigma )$，并且一定存在某种定义方式，只需要自由度为3的变量，就能定义能量密度函数$\Psi$。使用$F$的特征值当然是一种办法，但其非常不方便，所以这里定义了另外3个线性无关的变量，被称作各向同性不变量(isotropic invariants)：

注：没有下标的$I$均表示单位矩阵，有下标的表示各向同性不变量

$$\begin{array}{rl}{I}_1(F)& =\text{tr}({\Sigma }^2)=\text{tr}(F^{T}F)\\ I_2(F)& =\text{tr}({\Sigma }^4)=\text{tr}\left[(F^{T}F{)}^2\right]\\ I_3(F)& =\text{det}({\Sigma }^2)=(\text{det}F{)}^2\end{array}$$
对这3个变量求微分可以得到：
$$\begin{array}{rl}\delta I_1& =2(I:F:\delta F)=2F:\delta F\\ \delta I_2& =4\text{tr}\left(F^{T}F{F}^T\delta F\right)=4I:F^{T}F{F}^T\delta F=F{F}^{T}F:\delta F\\ \delta I_3& =2\text{det}(F)\delta [\text{det}F]=2(\text{det}F{)}^2(F^T{)}^{-1}:\delta F\end{array}$$
其中$I_3$用了行列式微分

现在可以定义Neohookean模型了：
$$\Psi (I_1,I_3)=\frac{\mu }{2}\left[I_1-\log (I_3)-3\right]+\frac{\lambda }{8}{\log }^2(I_3)$$
此时PK1数很好求：
$$\begin{array}{rl}P& =\frac{\partial \Psi }{\partial F}\\ & =\frac{\mu }{2}\left(\frac{\partial I_1}{\partial F}-\frac{1}{I_3}\frac{\partial I_3}{\partial F}\right)+\frac{\lambda \log (I_3)}{4I_3}\frac{\partial I_3}{\partial F}\\ & =\mu \left(F-F^{-T}\right)+\frac{\lambda }{2}\log (I_3)F^{-T}\end{array}$$
Neohookean模型保证了旋转无关，各向同性，其能处理强压缩，虽然容易数值爆炸，因为$I_3=J^2$，当压缩力很大时，体积变化分数$J\to 0$，会导致能量中的$\log$趋于无穷大，能量也非常大。

各种弹性能量模型对比

借用课程上的一张表

名称	$\Psi$	$P$	效率	旋转无关	各向同性	能处理强压缩
线性模型	$\mu \text{tr}({ϵ}^2)+\frac{\lambda }{2}{\text{tr}}^2(ϵ)$	$\mu (F+F^T-2I)+\lambda \text{tr}(F-I)I$	高	否	否	否
StVK	$\mu \text{tr}(E^2)+\frac{\lambda }{2}{\text{tr}}^2(E)$	$F(2\mu E+\lambda \text{tr}(E)I)$	低	是	是	否
Corotated	$\mu |S-I{|}_F^2+\frac{\lambda }{2}{\text{tr}}^2(S-I)$	$2\mu (F-R)+\lambda \text{tr}(R^{T}F-I)R$	中	是	是	否
Neohookean	$\frac{\mu }{2}\left[I_1-\log (I_3)-3\right]+\frac{\lambda }{8}{\log }^2(I_3)$	$\mu \left(F-F^{-T}\right)+\frac{\lambda }{2}\log (I_3)F^{-T}$	低	是	是	是

有限元方法离散化

在前面有关弹性体的所有推导中，都是将弹性体视为一个拥有无限点的三维区域，这使得计算机无法进行仿真。有限元方法的目的就是用有限的元素去拟合一个无穷的区域，在这里，我们将三维弹性体视为若干个四面体元素：

在四面体内部，变换函数将变成线性函数：$\hat{\varphi }(X)=AX+b$，因此变换梯度也变得简单：$F=A$. 并且$F$可以使用四面体上的四个点解方程解出来：
$$\begin{array}{rl}\left[\begin{array}{ccc}{\text{x}}_1-{\text{x}}_4& {\text{x}}_2-{\text{x}}_4& {\text{x}}_3-{\text{x}}_4\end{array}\right]& =F\cdot \left[\begin{array}{ccc}{X}_1-X_4& X_2-X_4& X_3-X_4\end{array}\right]\\ D_s& =F\cdot D_m\\ \Rightarrow F& =D_s{D}_m^{-1}\end{array}$$
令$W$为四面体的体积，可以计算得到$W=\frac{1}{6}\left|\text{det}{D}_m\right|$

则四面体内部$T_i$的弹性势能为：
$$E_i={\int }_{T_i}\Psi (F_i)\mathrm{d}X=W_i\Psi (F_i)$$
每一个四面体都会对它的4个顶点施加弹力，对每一个顶点需要计算它相关的所有四面体对它贡献的弹力，第$i$个四面体对其第$j$个顶点的贡献为$f_i^j=-\frac{\partial E_i}{\partial {\text{x}}_j}$

令$H_i=[f_i^1{f}_i^2{f}_i^3]$，则：
$$\begin{array}{rl}{f}_i^j& =-\frac{\partial E_i}{\partial {\text{x}}_j}\\ & =-\frac{\partial E_i}{\partial \Psi }\frac{\partial \Psi }{\partial F_i}\frac{\partial F_i}{\partial {\text{x}}_j}\\ & ={\left[-W_{i}P(F_i)D_m^{-T}\right]}_{ji}\\ \Rightarrow H_i& =-W_{i}P(F_i)D_m^{-T}\end{array}$$
对于四面体第四个顶点：$f_i^4=-f_i^1-f_i^2-f_i^3$，因为弹性内力要保证整个四面体合力为零

由此可以算出弹性体分成四面体元素后，内部每一个顶点的受力

时间积分

前文已经详细讲述了如何计算通过将弹性体视为四面体后计算每个顶点的受力，知道受力后就可以很方便的使用显示时间积分进行仿真，但隐式时间积分仍然比较困难。本节介绍弹性体仿真时间积分的处理方式，以及一些算法实践上的具体处理。

显示时间积分

以下符号，向量都代表整个弹性体所有点，即$m$个点，如$\text{x}$为$3m$维

对每一个节点进行如下操作：
$$\begin{array}{rl}{\text{x}}_{n+1}& ={\text{x}}_n+{\text{v}}_{n+1}\Delta t\\ {\text{v}}_{n+1}& ={\text{v}}_n+M^{-1}\left[f_{int}({\text{x}}_n)+f_{damp}({\text{v}}_n)+f_{ext}\right]\Delta t\end{array}$$
其中$f_{int}$表示内力，就是弹性体内部的弹力，需要用前文所述的各种能量计算出来

$f_{damp}$表示阻尼力，与速度有关，用于能量损耗

$f_{ext}$为外力，一般与弹性体形态无关，很容易计算，如重力

隐式时间积分

需要计算如下方程：
$$\begin{array}{rl}{\text{x}}_{n+1}& ={\text{x}}_n+{\text{v}}_{n+1}\Delta t\\ {\text{v}}_{n+1}& ={\text{v}}_n+M^{-1}\left[f_{int}({\text{x}}_{n+1})+f_{damp}({\text{v}}_{n+1})+f_{ext}\right]\Delta t\end{array}$$
对于阻尼力 $f_{damp}$，如果难以处理，也可以使用$f_{damp}({\text{v}}_n)$做半隐式积分。

对于内力$f_{int}({\text{x}}_{n+1})$，一般采用泰勒展开近似：(省略了下标)
$$f({\text{x}}_{n+1})\approx f({\text{x}}_n)+\frac{\partial f}{\partial \text{x}}{|}_{{\text{x}}_n}({\text{x}}_{n+1}-{\text{x}}_n)$$
为此我们需要求解刚度矩阵：$K({\text{x}}_n)=-\frac{\partial f}{\partial \text{x}}{|}_{{\text{x}}_n}$，这个刚度矩阵是一个$3m\times 3m$的矩阵，但我们计算时一般只考虑一个四面体，一个四面体至少需要考虑到3个顶点，那么算法运行时需要用到一个$3\times 3\times 3\times 3$的矩阵，这依然是一个比较大的运算量。实现时，可以直接将这个巨型矩阵直接算出来（比如VegaFEM）；也可以用隐式计算的方法，直接计算 $K\cdot w$，只需要在求微分$\delta K$之后，把里面的所有$\delta \text{x}$换成$w$即可。

现在来考察一下$K$，通过对力$f$求微分来推导：
$$\begin{array}{rl}K({\text{x}}_n)\delta \text{x}& =\frac{\partial f}{\partial \text{x}}\delta \text{x}=\delta f\\ \delta H& =\left[\begin{array}{ccc}\delta f_1& \delta f_2& \delta f_3\end{array}\right]\\ & =-W\delta P(F)D_m^{-T}\\ \delta P(F)& =\{\begin{array}{ll}\delta F\left[2\mu E+\lambda \text{tr}(E)I\right]+F\left[2\mu \delta E+\lambda \text{tr}(\delta E)I\right]& \text{if using StVK model}\\ \mu \delta F+\left[\mu -\lambda \log (J)\right]F^{-T}\delta F^T{F}^{-T}+\lambda \text{tr}(F^{-1}\delta F)F^{-T}& \text{if using Neohookean model}\end{array}\\ \delta F& =(\delta D_s)D_m^{-1}\\ \delta D_s& =\left[\begin{array}{ccc}\delta {\text{x}}_1-\delta {\text{x}}_4& \delta {\text{x}}_2-\delta {\text{x}}_4& \delta {\text{x}}_3-\delta {\text{x}}_4\end{array}\right]\end{array}$$

注：$J=\sqrt{I_3}=\text{det}F$是体积变化分数

根据以上公式可以对任意弹性模型计算$K({\text{x}}_n)\cdot w$，只需要最终在$\delta D_s$中，把$\delta \text{x}$替换为对应位置的$w$即可。在Siggraph 2012的FEM course中推荐的就是这个计算$K$的方法。

VegaFEM的实现方法

令 $\Delta \text{x}={\text{x}}_{n+1}-{\text{x}}_n,\Delta \text{v}={\text{v}}_{n+1}-{\text{v}}_n$

对于阻尼力，令$f_{damp}({\text{v}}_{n+1})=({\alpha }_1\cdot (-K({\text{x}}_n))+{\alpha }_2\cdot M)\cdot {\text{v}}_{n+1}=-D\cdot {\text{v}}_{n+1}$

则
$$\begin{array}{rl}\Delta \text{v}& =\Delta t{M}^{-1}\left[f_{int}({\text{x}}_n)-K({\text{x}}_n)\cdot \Delta \text{x}-D\cdot {\text{v}}_{n+1}\right]\\ M\cdot \Delta \text{v}& =\Delta t{f}_{int}({\text{x}}_n)-\Delta t^{2}K({\text{x}}_n)\cdot \Delta \text{v}-\Delta tD({\text{v}}_n+\Delta \text{v})\\ \left[\Delta t^{2}K({\text{x}}_n)+\Delta tD+M\right]\cdot \Delta \text{v}& =\Delta t\left[f_{int}({\text{x}}_n)-(\Delta tK({\text{x}}_n)+D){\text{v}}_n\right]\end{array}$$
方程已经变成了$AX=b$的形式，可以使用各种方式迭代解出$\Delta \text{v}$，比如下面Projective Dynamics将会详细讲的一种雅可比迭代法(Jacobi)

注： Siggraph 2012的FEM course中的方法与此类似，只不过公式的推导过程变成了求解$\Delta \text{x}$而不是$\Delta \text{v}$，与下面的Projective Dynamics也很类似。

Projective Dynamics (PD) 方法

PD算法的主要思路是，对每一个非线性约束，用投影的方式找到满足约束的位置，然后将约束视为到投影位置的某种距离（是个二次式），从而将整个非线性问题转化为一个二次优化问题。

比如弹性体中，四面体网格的弹性内力可以视为约束力，通过投影到最近的零势能位置（rest position），就可以转化为二次优化问题。

但是，仔细考虑就可以发现，这种投影方式本质上就是之前提到过的：将非线性的弹力计算函数用一阶泰勒展开近似。

下面来推导一下：
$$\begin{array}{rl}{\text{x}}_{n+1}& ={\text{x}}_n+{\text{v}}_{n+1}\Delta t\\ {\text{v}}_{n+1}& ={\text{v}}_n+M^{-1}\left[f_{int}({\text{x}}_{n+1})+f_{ext}\right]\Delta t\\ \Rightarrow {\text{x}}_{n+1}& ={\text{x}}_n+\Delta t{\text{v}}_n+\Delta t^2{M}^{-1}\left[f_{int}({\text{x}}_{n+1})+f_{ext}\right]\\ \frac{1}{\Delta t^2}& M\left({\text{x}}_{n+1}-{\text{x}}_n-\Delta t{\text{v}}_n-\Delta t^2{M}^{-1}{f}_{ext}\right)=f_{int}({\text{x}}_{n+1})\\ 令{\hat{\text{x}}}_n& ={\text{x}}_n+\Delta t{\text{v}}_n+\Delta t^2{M}^{-1}{f}_{ext}\\ \frac{1}{\Delta t^2}M\left({\text{x}}_{n+1}-{\hat{\text{x}}}_n\right)& =f_{int}({\text{x}}_{n+1})\approx K({\text{x}}^{(k)})\cdot \left({\text{x}}_{n+1}-{\text{x}}^{(k)}\right)+f_{int}({\hat{\text{x}}}_n)\end{array}$$

假设我们有一个迭代求解序列 ${\text{x}}^{(0)},...,{\text{x}}^{(k)}$，使得其越来越逼近于 ${\text{x}}_{n+1}$，并且初始 ${\text{x}}^{(0)}={\hat{\text{x}}}_n$

我们可以将方程写为：

$$\left(\frac{1}{\Delta t^2}M-K({\text{x}}^{(k)})\right)\cdot {\text{x}}^{(k+1)}=\frac{1}{\Delta t^2}M{\hat{\text{x}}}_n+f_{int}({\text{x}}^{(k)})-K({\text{x}}^{(k)}){\text{x}}^{(k)}$$

此时求解 ${\text{x}}^{(k+1)}$已经是$AX=b$的形式了，接下来讲一讲迭代求解。

令 $A=B-C$， 则
$$\begin{gathered} (B-C)X=b \\ BX-CX=b \\ BX=CX+b \\ X=B^{-1}(CX+b) \end{gathered}$$
使用一个迭代序列 $X^{(0)},...,X^{(k)}$，令：
$$X^{(k+1)}=B^{-1}(C{X}^{(k)}+b)$$

一般我们取$B$为$A$的对角元素，因为往往物理方程上面$A$的对角元素都比其他元素大，占主要部分，这样这个序列会更快收敛到方程的解。

我们计算一下$X^{(k+1)}-X^{(k)}$：
$$\begin{gathered} X^{(k+1)}=B^{-1}(B-A)X^{(k)}+B^{-1}b \\ {X}^{(k+1)}-X^{(k)}=B^{-1}(b-AX) \end{gathered}$$

现在我们代入到之前的隐式欧拉积分方程：
A = 1 Δ t 2 M − K ( x ( k ) ) B = diag { A } X ( k ) = x ( k ) b = 1 Δ t 2 M x ^ n + f i n t ( x ( k ) ) − K ( x ( k ) ) x ( k ) x ( k + 1 ) − x ( k ) = B − 1 ( 1 Δ t 2 M x n ^ + f i n t ( x ( k ) ) − K ( x ( k ) ) x ( k ) − 1 Δ t 2 M x ( k ) + K ( x ( k ) ) x ( k ) ) x ( k + 1 ) − x ( k ) = B − 1 ( 1 Δ t 2 M ( x n ^ − x ( k ) ) + f i n t ( x ( k ) ) ) \begin{align} A&=\frac 1 {\Delta t^2} M - K(\textbf{x}^{(k)})\\ B&=\text{diag}\{A\} \\ X^{(k)}&=\textbf{x}^{(k)}\\ b&=\frac 1 {\Delta t^2} M \hat{\textbf{x}}_n + f_{int}(\textbf{x}^{(k)}) - K(\textbf{x}^{(k)})\textbf{x}^{(k)} \end{align} \\ \begin{align} \textbf{x}^{(k+1)} - \textbf{x}^{(k)} &= B^{-1}\left( \frac 1 {\Delta t^2} M \hat{\textbf{x}_n} + f_{int} (\textbf{x}^{(k)})-K(\textbf{x}^{(k)})\textbf{x}^{(k)} - \frac 1 {\Delta t^2} M \textbf{x}^{(k)} + K(\textbf{x}^{(k)})\textbf{x}^{(k)}\right) \\ \textbf{x}^{(k+1)} - \textbf{x}^{(k)} &= B^{-1}\left( \frac 1 {\Delta t^2} M \left(\hat{\textbf{x}_n} - \textbf{x}^{(k)}\right) + f_{int} (\textbf{x}^{(k)}) \right) \end{align} ABX(k)b​=Δt21​M−K(x(k))=diag{A}=x(k)=Δt21​Mx^n​+fint​(x(k))−K(x(k))x(k)​​x(k+1)−x(k)x(k+1)−x(k)​=B−1(Δt21​Mxn​^​+fint​(x(k))−K(x(k))x(k)−Δt21​Mx(k)+K(x(k))x(k))=B−1(Δt21​M(xn​^​−x(k))+fint​(x(k)))​​

最终等式右边以全部是已知量，直接迭代求解即可。

还可以参考这篇文章使用切比雪夫多项式加速：A Chebyshev Semi-Iterative Approach for Accelerating Projective and Position-based Dynamic

计算出${\text{x}}^{(k+1)}-{\text{x}}^{(k)}$之后，还可以进一步使用线搜索(line search)算法来计算迭代步长，进一步优化收敛速度

Incremental Potential Contact (IPC) 方法

$$\begin{array}{rl}{\text{x}}_{n+1}& ={\text{x}}_n+{\text{v}}_{n+1}\Delta t\\ {\text{v}}_{n+1}& ={\text{v}}_n+M^{-1}\left[f_{int}({\text{x}}_{n+1},{\text{v}}_{n+1})+f_{ext}\right]\Delta t\\ \Rightarrow {\text{x}}_{n+1}& ={\text{x}}_n+\Delta t{\text{v}}_n+\Delta t^2{M}^{-1}\left[f_{int}({\text{x}}_{n+1},{\text{v}}_{n+1})+f_{ext}\right]\\ {\text{x}}_{n+1}& -\left({\text{x}}_n+\Delta t{\text{v}}_n+\Delta t^2{M}^{-1}{f}_{ext}\right)-\Delta t^2{M}^{-1}{f}_{int}({\text{x}}_{n+1},{\text{v}}_{n+1})=0\\ 令{\hat{\text{x}}}_n& ={\text{x}}_n+\Delta t{\text{v}}_n+\Delta t^2{M}^{-1}{f}_{ext}\\ M({\text{x}}_{n+1}& -{\hat{\text{x}}}_n)-\Delta t^2{f}_{int}({\text{x}}_{n+1},{\text{v}}_{n+1})=0\end{array}$$

我们将其转为一个优化问题，即最小化：
$$\begin{gathered} E(\text{x})=\frac{1}{2}{\Vert \text{x}-{\hat{\text{x}}}_n\Vert }_M+\Delta t^2\Psi (\text{x}) \\ 因为E^{\prime }(\text{x})=M({\text{x}}_{n+1}-{\hat{\text{x}}}_n)-\Delta t^2{f}_{int}({\text{x}}_{n+1},{\text{v}}_{n+1}) \\ 则只需求解{\text{x}}_{n+1}={\text{argmin}}_{\text{x}}E(\text{x}) \end{gathered}$$
$E(\text{x})$被称为 Increment Potential，可以看出$\frac{1}{2}{\Vert \text{x}-{\hat{\text{x}}}_n\Vert }_M$与惯性势能相关，$\Delta t^2\Psi (\text{x})$与弹性势能有关。优化问题的目的就是找到一个势能最小的位置作为下一时间步的状态。注意到这个$E(\text{x})$还可以添加其他能量包括碰撞，摩擦等。

IPC使用牛顿-拉夫逊方法结合线搜索(line search)迭代优化$E(\text{x})$，即
$$H_E(\text{x})\cdot v=-D_E(\text{x})$$
其中$H_E(\text{x})$为$E$的二阶导（海塞矩阵），$D_E$为一阶导，这里面涉及到对$\Psi$求二阶导

求解出$v$后作为搜索的方向，使用线搜索结合连续碰撞检测(CCD)，找到最佳步长进行移动，重复这个步骤直到时间步长加起来达到一个仿真步。

参考资料

FEM simulation of 3D deformable solids Siggraph 2012 Course

A Chebyshev Semi-Iterative Approach for Accelerating Projective and Position-based Dynamic

Projective Dynamics: Fusing Constraint Projections for Fast Simulation

VegaFEM

IPC

北京大学可视计算与交互概论