【论文复现】Taylor算法用于TOA（到达时间）的三维标签位置解算，360个标签、12个基站的环境作为验证，附MATLAB例程

本文给出论文《基于Taylor-Chan算法的改进UWB室内三维定位方法》中的Taylor算法来解算TOA的复现程序（MATLAB）。
使用论文中给定的12个锚点/360个测试的标签用来测试算法性能

运行结果

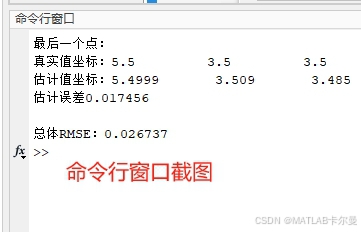
误差输出：

程序介绍

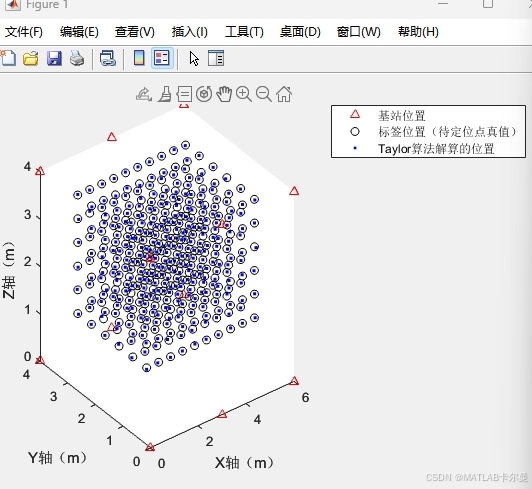
本程序基于 Taylor 迭代算法，实现了对三维空间内360个目标点的 TOA（Time of Arrival）定位解算，共配置 12个基站（锚点），支持仿真定位精度评估、误差可视化与迭代过程分析。

该方法参考文献《基于Taylor-Chan算法的改进UWB室内三维定位方法》，适用于室内超宽带（UWB）定位、导航系统等领域。

🧠 核心功能概述

功能模块	描述
基站配置	12 个固定基站，分布于 $3\times 2\times 2$ 的三维空间立方体顶点。
标签点生成	在$x\in [1,5.5],y\in [1,3.5],z\in [1,3.5]$范围内以 0.5m 网格生成 360 个测试点。
TOA建模	利用三维欧氏距离模拟从标签到各基站的传播时间，加入高斯白噪声模拟测距误差： $r_i=|\mathbf{p}-{\mathbf{s}}_i|+\mathcal{N}(0,{\sigma }^2)$
Taylor迭代定位	以基站位置均值作为初始值，构造雅可比矩阵进行迭代更新： ${\mathbf{p}}_{k+1}={\mathbf{p}}_k+({\mathbf{A}}^T\mathbf{A}{)}^{-1}{\mathbf{A}}^T\mathbf{B}$ 直至误差小于阈值 $\varepsilon$。
误差统计	计算所有标签点的估计误差，并输出 RMSE（均方根误差），分析算法整体精度。
可视化结果	生成 3D 图像，展示基站位置、标签真值与估计点；同时绘制 Taylor 迭代收敛误差曲线。

📊 结果输出

• 每个点定位误差（最后一个点）
• 所有点定位 RMSE：$\text{RMSE}=\sqrt{\frac{1}{N}{\sum }_{i=1}^N\Vert {\hat{\mathbf{p}}}_i-{\mathbf{p}}_i{\Vert }^2}$
• 迭代误差收敛曲线

📁 应用场景

• 室内 UWB 定位系统建模
• 导航/无人系统仿真教学
• TOA 定位算法性能对比
• 三维定位精度评估实验

MATLAB源代码

部分代码如下：

% Taylor方法解算TOA，定位三维目标、12个锚点/360个测试的标签
% 参考文献:《基于Taylor-Chan算法的改进UWB室内三维定位方法》
% 2025-07-05/Ver1
%% 初始化与
clc;clear;close all;
rng(0);
% 定义参数和待测点位置
num_stations = 12; % 基站数量（锚点数量）
std_var1 = 1e-10; %TOA时间误差（标准差）
% 固定基站位置
stations_position = [
    0,0,0;
    3,0,0;
    6,0,0;
    0,4,0;
    3,4,0;
    6,4,0;
    0,0,4;
    3,0,4;
    6,0,4;
    0,4,4;
    3,4,4;
    6,4,4]; %按论文的基站坐标设置
c = 3e8;
% =====生成待定位点坐标=====
% 定义坐标范围
x = 1 : 0.5 : 5.5;  % 共10个，原论文有误
y = 1 : 0.5 : 3.5;  % 共6个，原论文有误
z = 1 : 0.5 : 3.5;  % 共6个，原论文有误

完整代码下载链接：
https://download.youkuaiyun.com/download/callmeup/91327939

如需帮助，或有导航、定位滤波相关的代码定制需求，请点击下方卡片联系作者