【论文复现】基于Taylor-Chan算法的TOA（到达时间）建模与解算例程，使用matlab代码复现，输出图像与RMSE

简介

本文对基于Taylor-Chan算法的UWB三维定位代码的复现过程与讲解，结合算法原理与实现细节进行分步解析。

程序复现过程

以下是对基于Taylor-Chan算法的UWB三维定位代码的复现过程与讲解，结合算法原理与实现细节进行分步解析：

算法原理概述

该代码实现了Taylor-Chan融合定位算法，结合了Taylor级数展开法的高精度迭代特性和Chan算法的最小二乘全局收敛优势。核心思想是：

1. Chan算法提供初始位置估计：通过构造非线性方程组的加权最小二乘解，快速获得全局近似解。
2. Taylor算法进行局部优化：以Chan的输出为初值，通过迭代线性化过程逼近真实位置。
3. 异常值筛选机制：基于残差分析筛选可靠基站，提高NLOS（非视距）环境下的定位精度。

代码复现过程

1. 初始化与参数设置

clc;clear;close all; rng(0);
num_stations = 12; % 12个基站三维布局
stations_position = [0,0,0; 3,0,0; ... ]; % 按论文布局
std_var2 = 1e-10*[1,1,..10,..1]'; % 模拟2个NLOS基站

• 基站布局：采用3D立方体分布（0-6m范围），符合典型室内定位场景。
• 误差模型：设置两个基站的高方差（10倍）模拟NLOS效应。

2. 待测点生成

x = 1:0.5:5.5; y=1:0.5:3.5; z=1:0.5:3.5;
[X,Y,Z] = meshgrid(x,y,z); positions = [X(:), Y(:), Z(:)];

生成360个测试点（10×6×6网格），覆盖基站网络中心区域，避免边缘效应。

3. TOA测距建模

delta = ones(num_stations,1)*position - stations_position;
r_ideal = sqrt(sum(delta.^2,2)); % 理想距离
r = r_ideal + std_var2.*randn(size(r_ideal))*c; % 添加噪声

通过理想距离+高斯噪声模拟TOA测量值，其中c=3e8为光速。

4. Taylor算法迭代

position_est = [1,1,1]'; % 初始估计
for i1 = 1:100
B = estimated_distance - measured_distance; % 残差向量
A = [∂x/∂d, ∂y/∂d, ∂z/∂d]; % 雅可比矩阵
Delta = (A'*A)\A'*B; % 最小二乘解
position_est += Delta; % 更新估计
end

• 雅可比矩阵：由几何偏导数构成，反映位置变化对距离的影响。
• 迭代终止条件：Δ的模长小于阈值ε=0.01。

. Chan算法求解

通过两步加权最小二乘估计目标坐标，处理TDOA方程的非线性。

6. Taylor-Chan融合策略

• 残差阈值J：动态计算为平均相对误差的100倍，用于排除NLOS影响。
• 二次定位：仅使用可靠基站重新运行Chan算法，提升精度。

关键代码解析

1. 异常值筛选逻辑

通过动态阈值识别异常测量值，比固定阈值更适应复杂环境。

2. Chan算法符号判断

position_est_Chan = sign(Z_alpha1(1:3)) .* sqrt(abs(Z_alpha2));

由于平方根导致符号丢失，通过Chan第一阶段解的符号确定坐标方向。

3. 可视化与误差分析

figure; plot3(...); % 3D位置分布
figure; plot(norm_err...); % 误差曲线
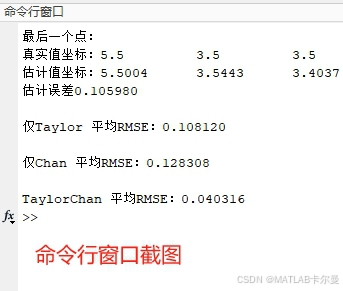
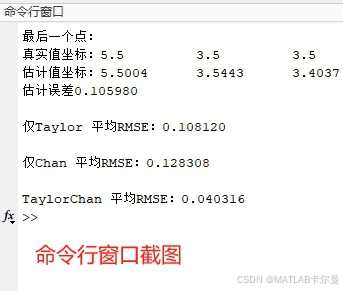
fprintf('TaylorChan 平均RMSE：%f\n',rms(...));

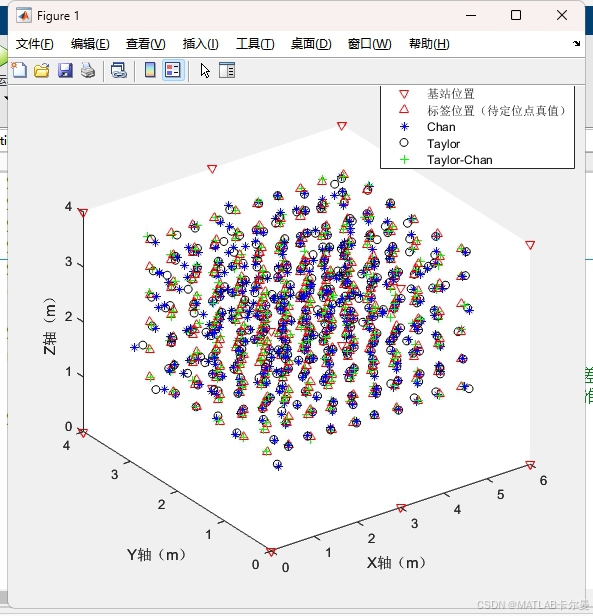
• 3D散点图：直观展示各算法定位结果的空间分布。
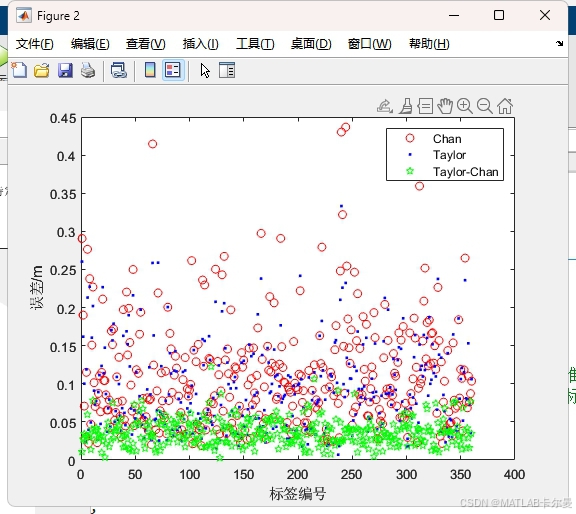
• 误差曲线：对比三种算法的逐点误差，突出融合算法优势。
  源代码有注释，未完全标注的算法细节可以在代码里面看

运行结果

定位结果示意图：

各标签定位误差对比：

命令行窗口输出的RMSE：

matlab代码

代码的结构如下：

部分代码内容：

% TaylorChan方法解算TOA，定位三维目标、12个锚点/360个测试的标签
% 参考文献:《基于Taylor-Chan算法的改进UWB室内三维定位方法》
% 作者：matlabfilter
% 2025-07-10/Ver1：从旁边的纯Taylor算法而来
%% 初始化与
clc;clear;close all;
rng(0);
% 定义参数和待测点位置
num_stations = 12; % 基站数量（锚点数量）
std_var1 = 1e-10*[1,1,1,1,1,1,1,1,1,1,1,1]'; %TOA时间误差（标准差）
std_var2 = 1e-10*[1,1,1,1,1,10,1,1,1,10,1,1]'; %TOA时间误差（标准差）【有两个点NLOS的情况】
% 固定基站位置
stations_position = [
    0,0,0;
    3,0,0;
    6,0,0;
    0,4,0;
    3,4,0;
    6,4,0;
    0,0,4;
    3,0,4;
    6,0,4;
    0,4,4;
    3,4,4;
    6,4,4]; %按论文的基站坐标设置
c = 3e8;
% =====生成待定位点坐标=====
% 定义坐标范围
x = 1 : 0.5 : 5.5;  % 共10个，原论文有误
y = 1 : 0.5 : 3.5;  % 共6个，原论文有误
z = 1 : 0.5 : 3.5;  % 共6个，原论文有误

% 生成网格
[X, Y, Z] = meshgrid(x, y, z);  % X为横坐标，Y为纵坐标
positions = [X(:), Y(:), Z(:)];  % 共360行，每行一个标签点的[x, y]坐标

c = 3e8;

完整代码：

如需帮助，或有导航、定位滤波相关的代码定制需求，请点击下方卡片联系作者