一、行列式的概念
1、排列
(1)把n个不同的元素排成一列,就称之为这n个元素的n级排列,简称排列,记为
![]()
(2)n个不同的元素共有种不同的n级排列,举例来说:
有3个元素——1、2、3,它们共有种排列,分别为“1 2 3”、“1 3 2”、“2 1 3”、“2 3 1”、“3 1 2”、“3 2 1”
2、逆序
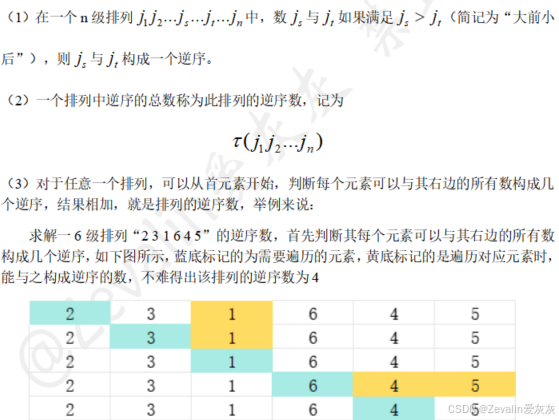
3、对换

4、奇排列与偶排列

5、行列式及对角线法则
(1)对于一个二阶行列式,其计算公式如下:
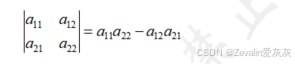
从“几何”上可以发现,行列式的结果为对角线“\”(称为主对角线)上的元素相乘的结果减去对角线“/”(称为副对角线)上的元素相乘的结果
(2)对于一个三阶行列式,其计算公式如下:
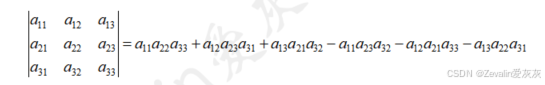
从“几何”上可以发现,行列式的结果为每条对角线“\”(下图红线)上的元素相乘的结果的和,减去每条对角线“/”(下图蓝线)上的元素相乘的结果的和
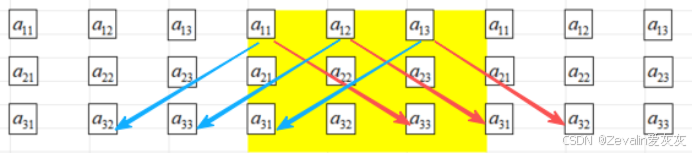
此外也能发现,结果表达式中每一项的元素均来自不同行不同列,且表达式的项数为,每一项前面可能带正号,也可能带负号
(3)n阶行列式的定义:

6、例题




二、行列式的性质
1、行列式的几个重要性质
(1)行列式的行与列互换,行列式的值不变,行列互换的表示如下所示。
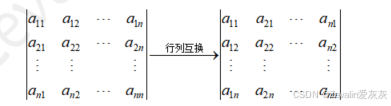
以三阶行列式为例进行证明,如下为两个三阶行列式的展开式,两个三阶行列式互为进行行列互换的结果,不难发现两个展开式是相等的
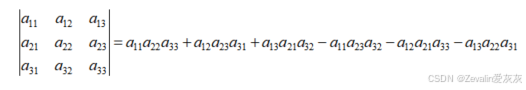
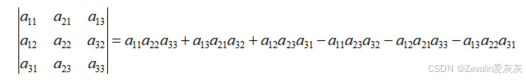
(2)行列式的某两行或某两列互换,每互换一次,行列式的值取一次相反数,第一行与第二行互换的表示如下所示,其它情况可以此类推。
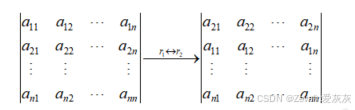
以三阶行列式为例进行证明,对
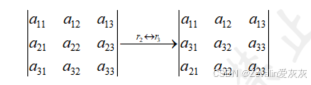
分别对变换前和变换后的行列式求解,有
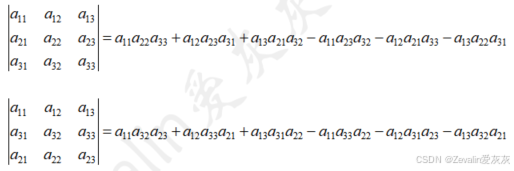
不难发现,
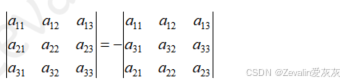
若行列式中有两行或两列(及以上)完全相同,则相同的两行或两列互换后仍为其本身,又因为互换一次后行列式的值取一次相反数,所以不难得出行列式的值为0
(3)行列式的某行或某列可以提公因子,提取第二行的公因子的表示如下所示,其它情况可以此类推。
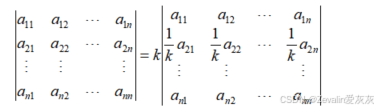
需注意公因子是按照一行或一列算的,没有对多行或多列提一个公因子的说法,若需要同时对多行或多列提公因子,需逐步进行,每一步提出的公因子相乘即可,如下所示
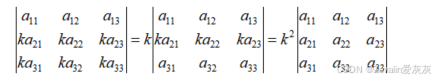
如果行列式的某行或某列的元素全为0,则对该行或该列提公因子,提出的公因子是0,不难得出行列式的值为0
(4)若行列式中有两行或两列(及以上)成比例,则行列式的值为0,第一行与第二行成比例的行列式及其结果如下所示,其它情况可以此类推。
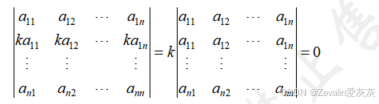
行列式的某行或某列可以提公因子,对成比例的几行或几列的其中一行/列提公因子,即可使行列式中原本成比例的两行或两列完全相同,而行列式中若有两行或两列(及以上)完全相同,则行列式的值为0
(5)若行列式中某行或某列的元素均为两数之和,则行列式可拆分为两个简单行列式之和,按某一行元素拆分的结果如下所示,其它情况可以此类推。
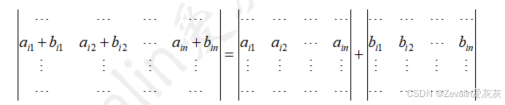
该性质可通过直接求解上式左右两边的展开式,再结合分配律得证
(6)把行列式的某行或某列的元素全部乘以k(任意非0常数)后加到另一行或列(不改变原本行或列的元素),行列式的值不变,这称为倍加变换,此性质常用于将行列式转换为三角形行列式(对角线的某一侧元素全为0),第一行倍加至第二行的变换如下所示,其它情况可以此类推。
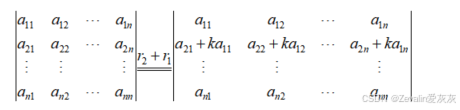
对倍加变换后的行列式做拆解,针对被倍加的行或列,将其拆分为原本的行或列和另一行或列乘以k的结果相加,前者为原行列式,后者结果为0,此性质得证
2、例题






三、行列式的展开定理
1、余子式与代数余子式


2、行列式的展开定理说明
(1)展开定理内容:


(2)定理说明:一个行列式等于其某行或某列的元素分别乘以其相应的代数余子式再求和。
(3)该定理不仅可以应用于行列式降阶,在特定情况下还可应用于行列式升阶,结合行列式的性质可更快地求解行列式的值。
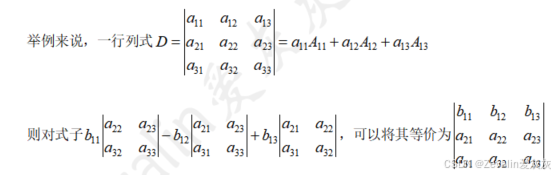
(4)一个行列式的某行或某列元素分别乘以另一行或列对应位置元素(列号或行号相同)的代数余子式再求和,结果必为0。
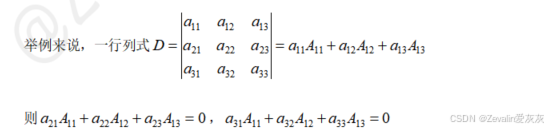
3、例题



四、几种典型行列式的计算
1、范德蒙德行列式
(1)范德蒙德行列式的特点:
①第1行或第1列的元素全为1。
②每列或每行元素可构成等比数列,公比在第2行或第2列。
③行列式的值等于所有公比元素通过两两组合作差再相乘的结果,对一个n阶范德蒙德行列式,有个公比作差项相乘,对公比元素两两组合得到每一乘数项对应的两个公比元素,列号或行号较大的公比元素减去列号或行号较小的公比元素,即为一个公比作差项,
个公比作差项相乘即为行列式的值。
(2)举例:



2、三对角线型行列式
(1)三对角线型行列式的特点:对角线和对角线周围“一步距离”的元素不为0,其余元素全为0。
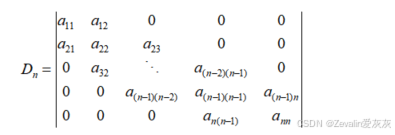
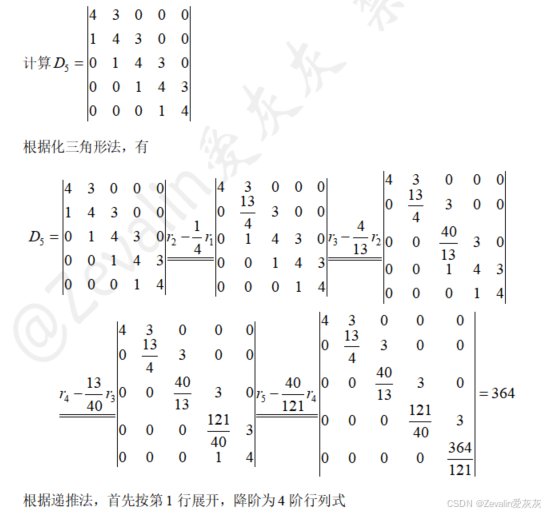
(2)求解三对角线型行列式的方法:

(3)举例:

3、分块行列式
(1)分块行列式的特点:行列式可横竖分为4块,其中一块中的元素全部为0。
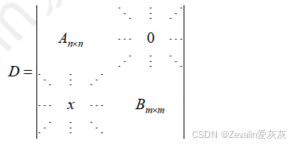
(2)拉普拉斯公式:
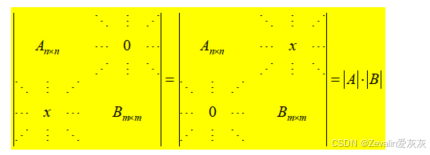
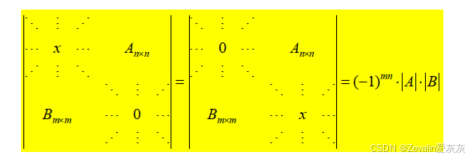
(3)举例:



五、克拉默法则
1、非齐次线性方程组与齐次线性方程组
(1)任意一个n元非齐次线性方程组均可表示为

(2)任意一个n元齐次线性方程组均可表示为

2、克拉默法则说明
(1)克拉默法则的内容:

(2)举例验证克拉默法则:

(3)关于克拉默法则的衍生结论:
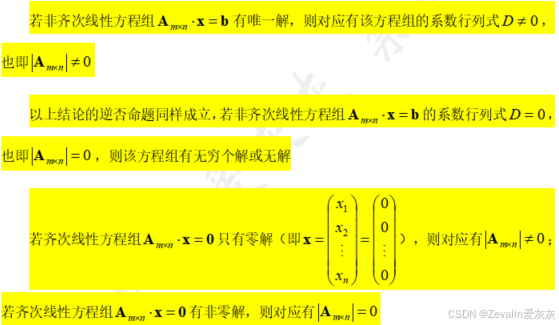
3、例题
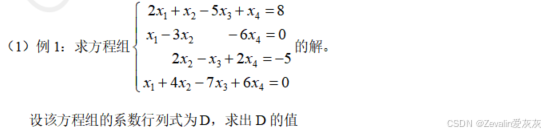


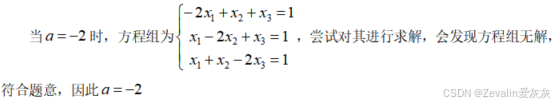























 1875
1875

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










