参考教程:
一、复数及复变函数的概念与复数代数运算
1、复数及复变函数的概念
(1)复数是一种数学概念,可表示为。
①x被称为复数的实部,它是复数的实数部分,可记为。
②y被称为复数的虚部,它是复数中伴随虚数单位i的系数(同样为实数),可记为。
③虚数单位i与实数的关系为。
④有时虚数单位也用j表示。
(2)复变函数是自变量为复数的函数。
2、复数及其代数运算
(1)关于复数的几个概念:

(2)任意两个复数之间不能比较大小(或者说不能直接比较大小),不过如果两个复数的实部和虚部均相等,则可认为两个复数相等,反之同样成立。
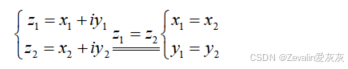
(3)复数的代数运算:
①加法与减法:两个复数的实部与虚部分别相加即可。
![]()
②乘法:按照多项式乘法法则计算即可。
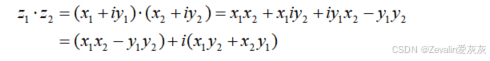
③除法:根据平方差公式将分母有理化,然后按照多项式乘法法则计算即可。
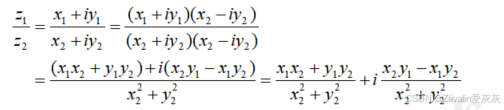
(4)共轭复数的性质:
①代数运算的性质:

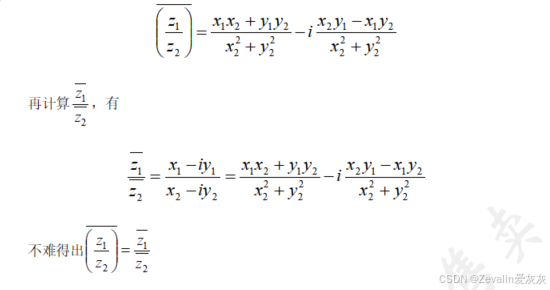
②对一个复数连续取两次共轭,结果为它本身,即,证明如下:
![]()
③一个复数与其共轭复数相乘,结果为复数的模平方,证明如下:
![]()
④一个复数与其共轭复数相加,结果实部为原本的两倍,虚部为0,而一个复数与其共轭复数相减,结果实部为0,虚部为原本的两倍,证明如下:
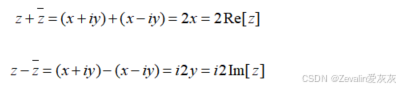
3、例题
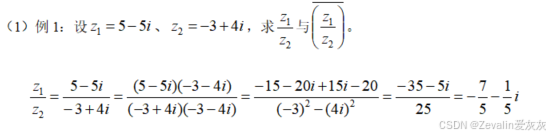

二、复数的几何意义
1、复数的其它表示方法
(1)复数可借助复平面表示,复平面的横轴为复数的实部(实轴),纵轴为复数的虚部(虚轴),如下图所示。
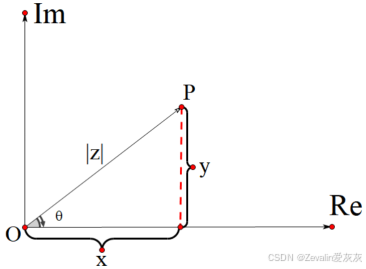
(2)辐角:

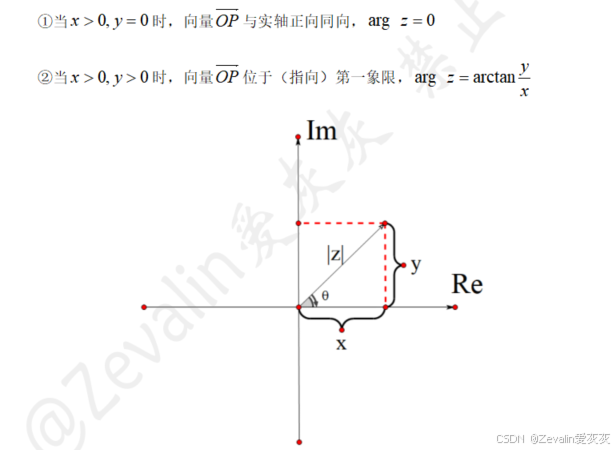

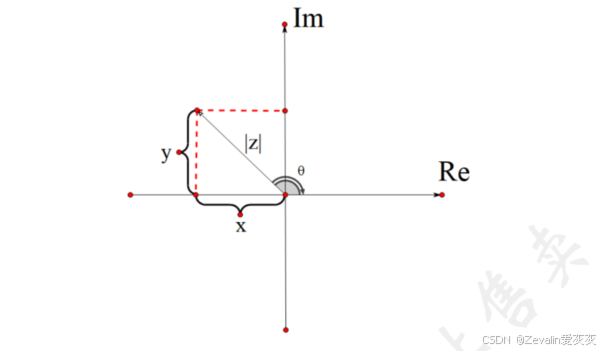
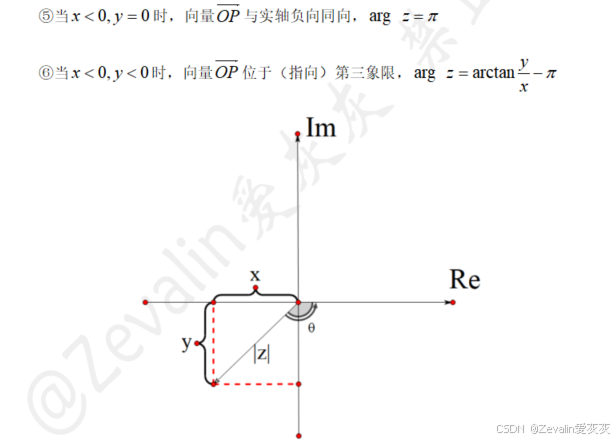

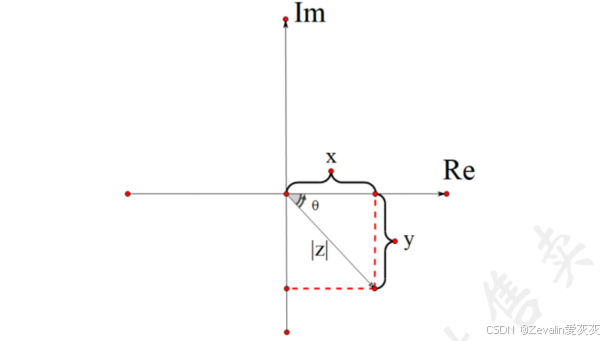
2、复数的表示方法
(1)几何表示法:
![]()
(2)向量表示法:
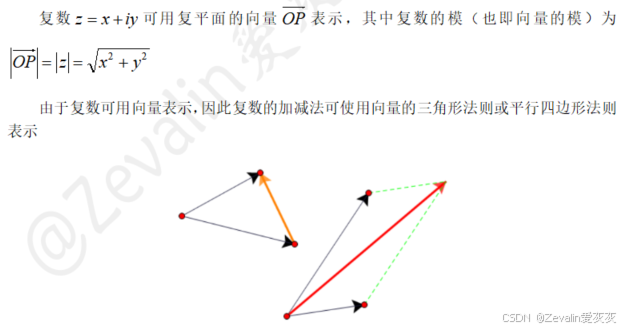

(3)三角表示法:
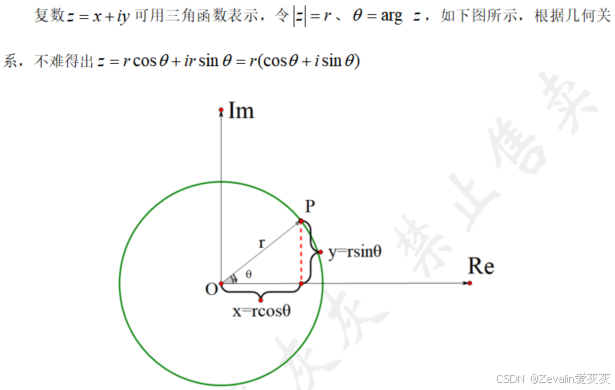
(4)指数表示法(极坐标表示法):

3、例题






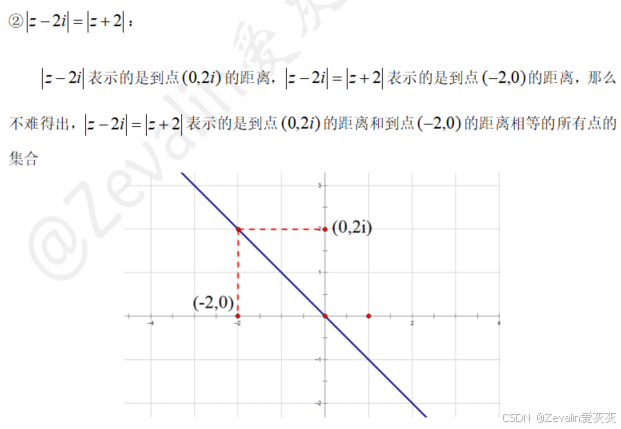
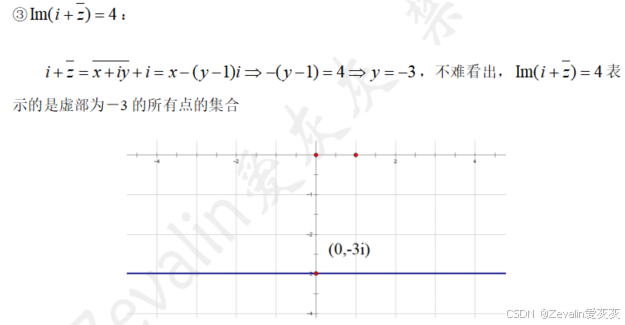
三、复数的乘幂与方根
1、乘积与商
(1)乘法:

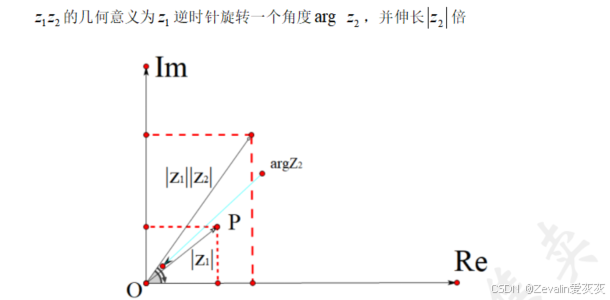
(2)除法:

(3)旋转因子:

2、幂与根
(1)z的n次幂:
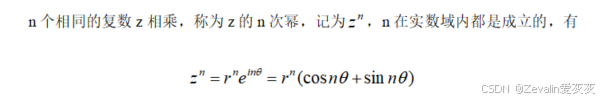
(2)z的n次方根:

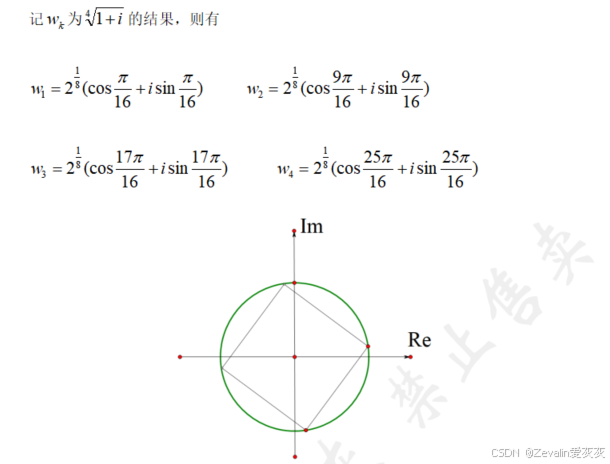
3、例题


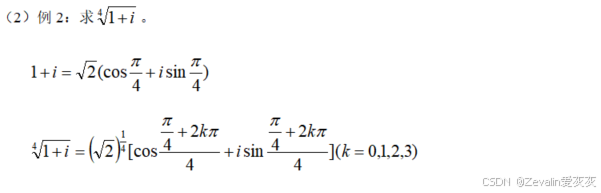
四、区域
1、区域的概念
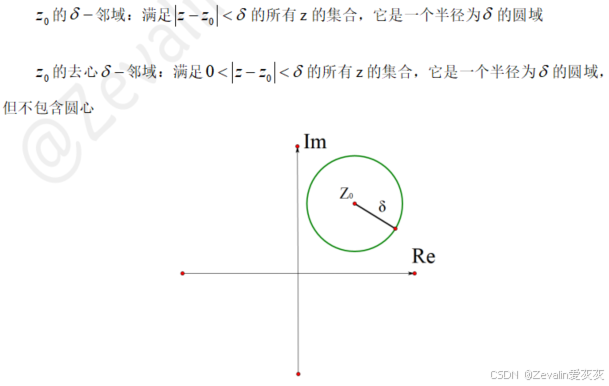
(1)邻域:
![]()
(2)内点:
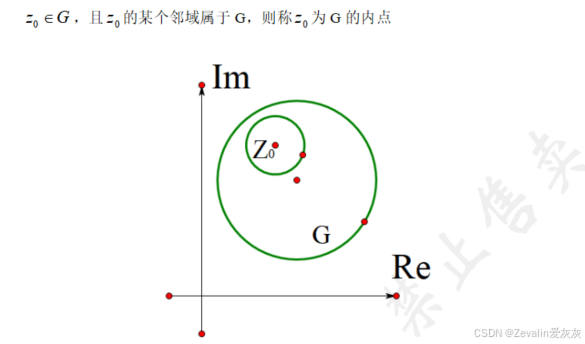
(3)开集:
一个集合内的每一个点都是其内点,称该集合为开集(可认为其边界上的点不属于集合中的点)
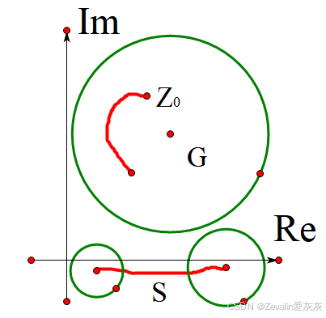
(4)连通集:
集合G内任意两点之间随意连线,总能有至少一条连线上的点都在集合G内,则称集合G为连通集,如下图所示,集合G为连通集,集合S为非连通集
(5)区域:
连通的开集称为区域
(6)边界点:
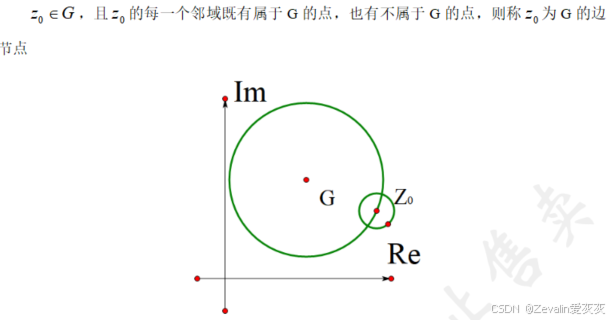
(7)闭区域:
区域与边界的合集称为闭区域,其中边界可能是曲线,也可能是孤立点
2、连通域
(1)简单闭曲线:

(2)光滑曲线:

(3)单连通域:
若属于区域G的任何简单闭曲线C的内部也属于G,则称G为单连通域,从几何上看,单连通域是一个无洞无割痕、由单个连通集组成的点集
属于单连通域的简单闭曲线在域内可以变形收缩成一个点
3、例题

五、复变函数介绍
1、复变函数的定义
(1)设G是复平面内的一个点集,如果存在一个确定的法则,对于G中的每一个复数,都有一个或者几个复数
与之对应,则称复变数w是复变数z的函数,记作
。
①单值:一个z对应w的一个值。
②多值:一个z对应w的两个或以上的值。
(2)一个复变函数确定了自变量为x、y的两个二元实函数。
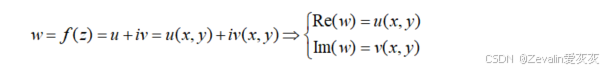
(3)由于复变函数涉及四个变量(x、y、u、v),因此不能用一个平面,也不能用三维空间中的几何图形表示复变函数,复变函数的本质是z平面上的一个点集(定义域集合)到w平面上的一个点集(值域集合)的一个映射。
2、映射

3、例题

六、复变函数的极限和连续性
1、复变函数的极限
(1)定义:

(2)几何意义:
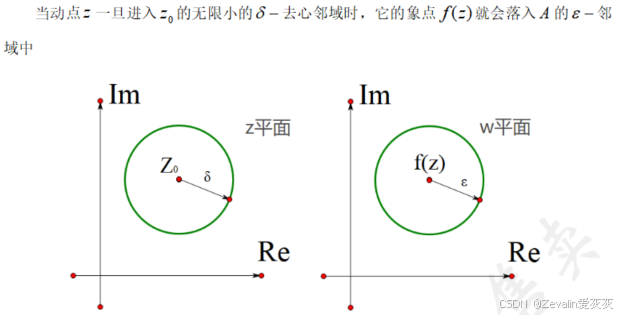
(3)极限的计算:
①给定函数求极限:

②极限满足的运算法则:

2、复变函数的连续性
(1)定义:

(2)衍生结论:

3、例题
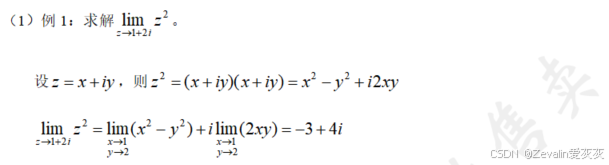

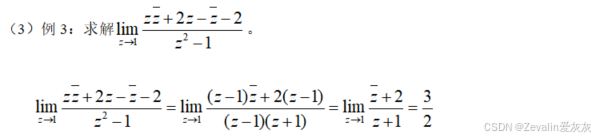























 717
717

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










