参考教程:
一、解析函数导论
1、复变函数的导数和微分
(1)导数的定义:

(2)可导与连续性的关系:
![]()
(3)求导法则:
由于复变函数中导数的定义与一元实变函数中导数的定义在形式上完全一致,并且复变函数中的极限运算法则也和实变函数中一样,因而实变函数中的求导法则都可以不加更改地推广到复变函数中来
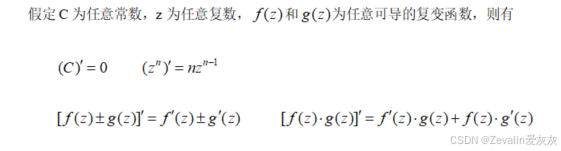

(4)微分的概念:

2、解析函数的概念
(1)解析函数的定义:

(2)奇点的定义:
![]()
(3)两个定理及衍生结论:


(4)连续、可导与解析的关系:
①当函数在某一点上:

②当函数在某一区域内:

3、例题



二、解析函数的充要条件
1、柯西-黎曼方程
(1)柯西-黎曼方程的定义:
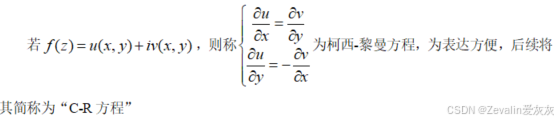
(2)定理1:

定理必要性证明如下:


定理充分性证明如下:

(3)定理2:

(4)定理1与定理2的意义:

(5)判断函数在某点是否可导、连续的基本步骤:

(6)判断函数在区域D内是否可导、连续的基本步骤:

2、例题





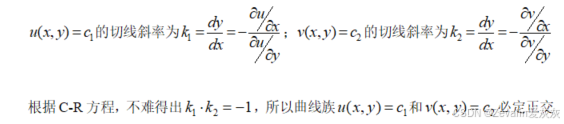
三、初等函数
1、指数函数
(1)指数函数的定义:

(2)指数函数的性质:

2、对数函数
(1)对数函数的定义:

(2)根据对数函数定义的引伸结论:

(3)对数函数的性质:

3、幂函数
(1)幂函数的定义:
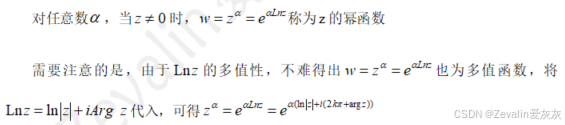
(2)不同的幂函数性质:


4、三角函数
(1)三角函数的定义:

(2)三角函数的性质:
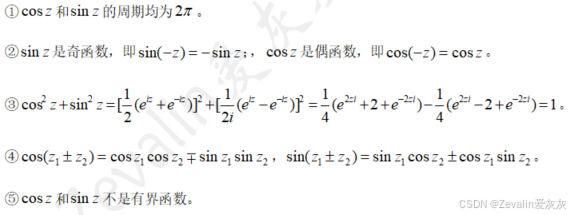
5、例题
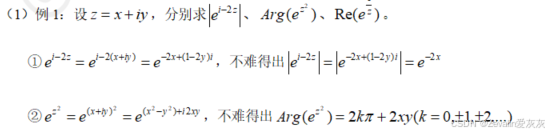
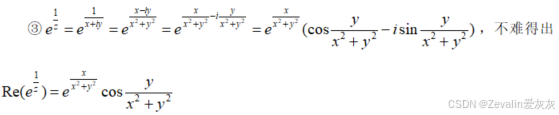


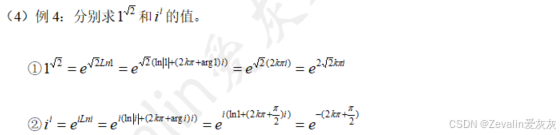
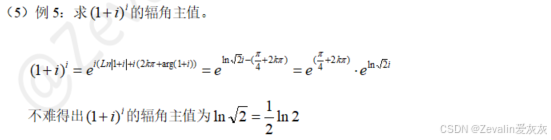
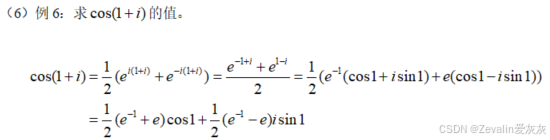






















 6622
6622

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










