自动控制原理 专题——传递函数与闭环控制理解

参考教程：

https://www.bilibili.com/video/BV1zVrQYnEKX/?spm_id_from=333.1387.favlist.content.click

https://www.bilibili.com/video/BV1JrreYMETM/?spm_id_from=333.1387.favlist.content.click

一、传递函数深入理解

1、拉氏变换回顾

2、频率响应简介

3、频率响应求解

4、频率响应的图解法

5、冲激响应与传递函数的关系

        传递函数从微分方程而来，它反映了系统的全部特性

        回顾卷积的知识，线性系统的冲激响应完全反映了线性系统的特性，也就是说，冲激响应和传递函数其实是同一个东西的一体两面

        在求得系统的冲激响应后，把输入的信号和系统的冲激响应进行卷积，就可以得到系统在零初值状态下的强迫响应

        在求得系统的传递函数后，把系统输入的拉氏变换和系统的传递函数进行相乘，就可以得到系统输出响应的拉氏变换，再进行拉式反变换即可得到系统的输出响应

        对于任何一个函数或者系统，都可以从时域和频域上去看它，通过对以上结论的观察，可以知道时域上的冲激响应和频域上的传递函数应该存在着联系，如下所示

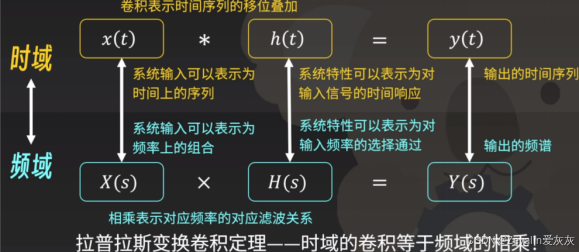
        很显然，系统的传递函数就是冲激响应的拉氏变换，如下所示，二者的关联为——冲激函数的频谱为1，包含了所有频率的特征

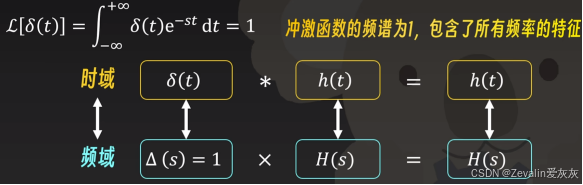
        所以，求系统冲激响应的方法又多了一种，求出系统的传递函数后做拉式反变换即可

6、Bode图

        要想直观地表示系统的频率响应，可以借助Bode图表示频率响应曲线，从曲线中可以获取幅频（振幅-频率）特性与相频（相位-频率）特性，如下所示，其中频率特性为对数坐标，幅频特性的纵轴为振幅（单位为分贝），相频特性的纵轴为相角

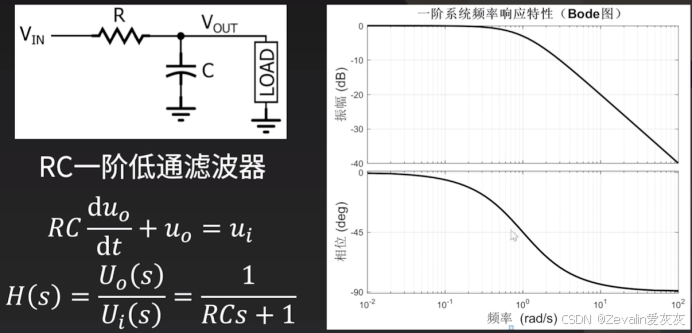
        为什么要关心相位？在反馈控制系统中，如果控制器获取的反馈信号存在较大的相位滞后（俗话说就是“慢半拍”），很容易导致负反馈和干扰叠加变成正反馈，从而引起系统不稳定

7、传递函数的零点和极点

        让传递函数取到无穷大值的s值称为极点，让传递函数取到0的s值称为零点，以下为几个例子

        极点和零点与系统的稳定性、动态响应密切相关

        将传递函数的极点画在复平面上，极点所处的位置将会反映系统的响应

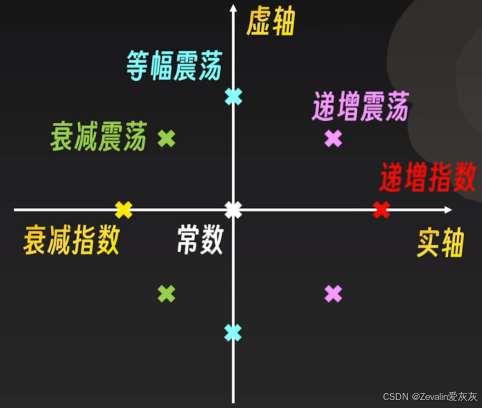
        系统在有限输入下，如果输出是有限（收敛）的，那么该系统是稳定的

        如果系统的传递函数中存在实部为正的极点，则说明系统的冲激响应存在指数上升的函数，则系统的冲激响应发散，也就是说系统不稳定；如果传递函数中存在实部为零的共轭复数极点，则系统在冲激响应下会出现无阻尼震荡，系统也是不稳定的；因此，系统稳定的必要条件是传递函数所有极点在坐标轴的左半平面

        零点影响系统的渐近稳态响应和动态特性

8、用MATLAB实现控制系统建模

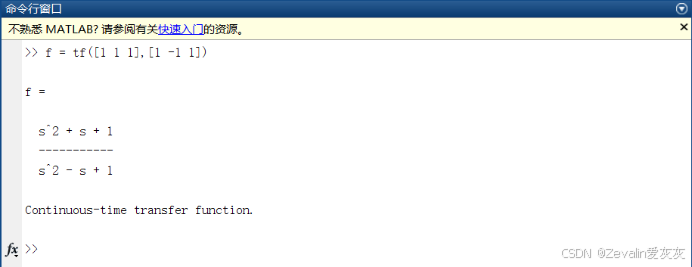
        tf函数构造一般形式传递函数：只要在第一个参数输入传递函数分子多项式系数矩阵，在第二个参数输入传递函数分母多项式系数矩阵，即可构造出一般形式传递函数

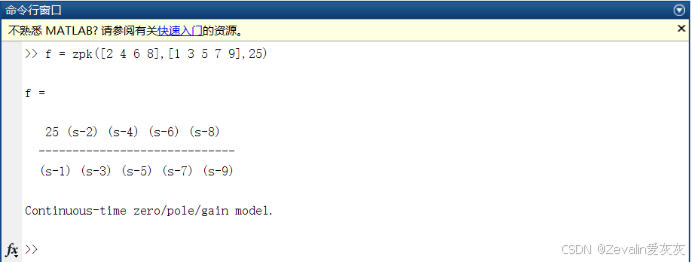
        zpk函数构造零极点增益形式传递函数：该函数的第一个参数是零点集，第二个参数是极点集，第三个参数是增益，zpk函数根据这三个参数构造出零极点增益形式传递函数

        构建传递函数后，使用“impulse(f)”可求传递函数的冲激响应，使用“step(f)”可求阶跃响应，使用“bode(f)”可求频率响应曲线，使用“pzplot(f)”可求系统零极点图

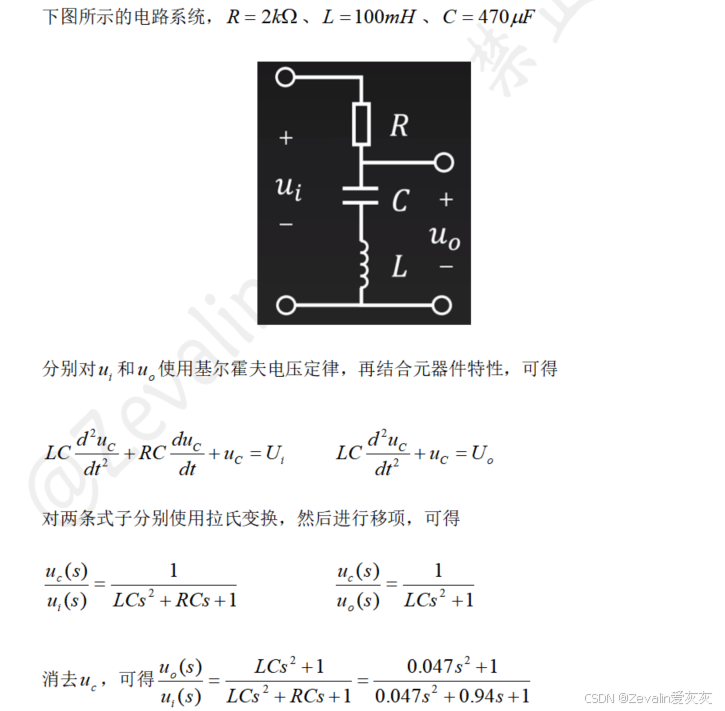
9、控制系统建模案例

        借助MATLAB可绘制该传递函数的Bode图，可以发现，当输入频率满足特定条件时，频率响应为负无穷，此时LC发生串联谐振，输出端短路，也就是说，该输入频率的信号基本无法通过此电路系统

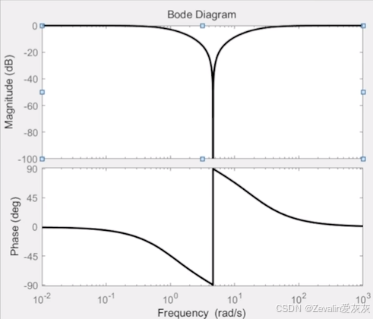
        通过以上分析可以得出，该电路为一个陷波器（带阻滤波器），可用于滤除某个固定频率上的信号

10、传递函数零极点和频率响应的关系

11、基本传递函数单元

        基本的比例环节、微分环节、积分环节如下所示

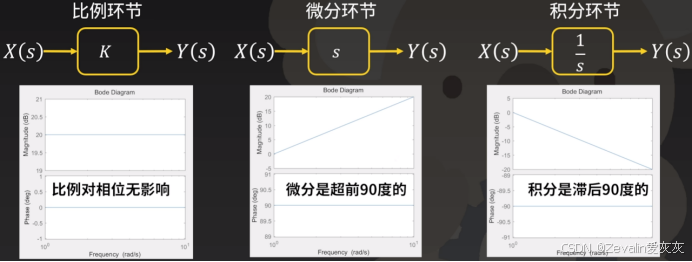
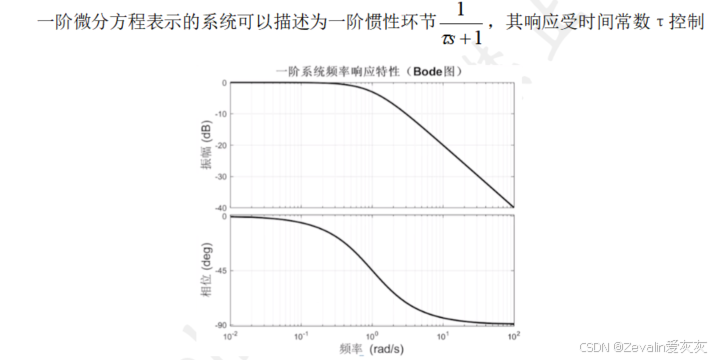
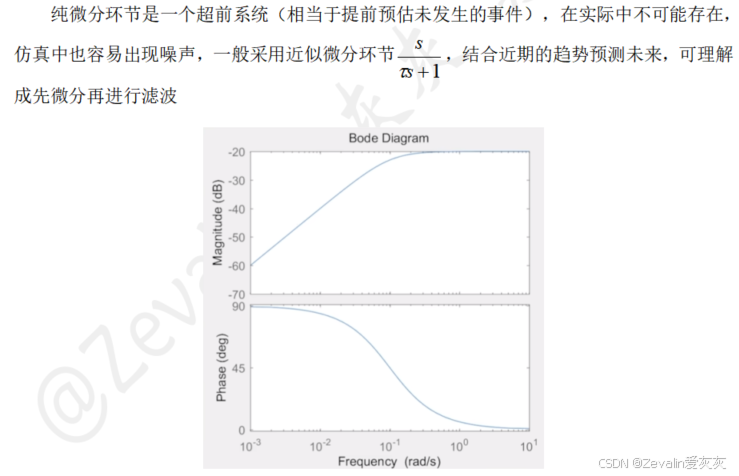
        二阶微分方程表示的系统，根据特征根的分布可分为多种情况，这在第三章中有详细介绍，此处不再赘述

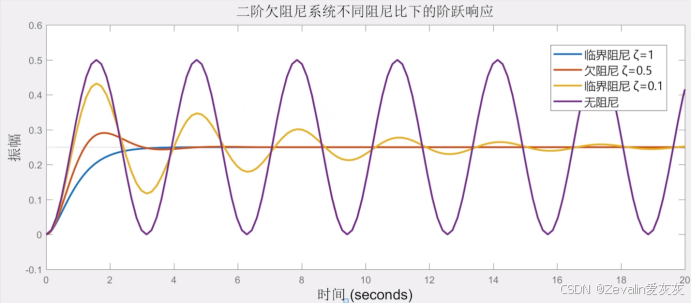
        二阶振荡系统对特定输入频率会产生放大效果（共振），阻尼越小共振越强，还是以MKB系统（弹簧-质量-阻尼力学系统）为例，逐渐减小阻尼B，可以发现放大效果越来越强

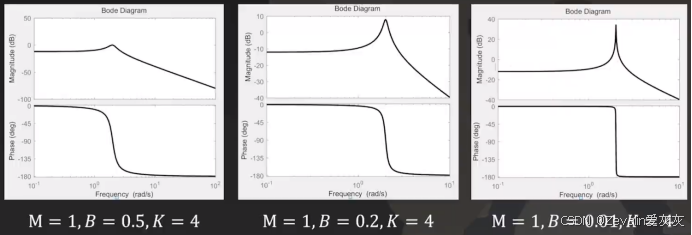
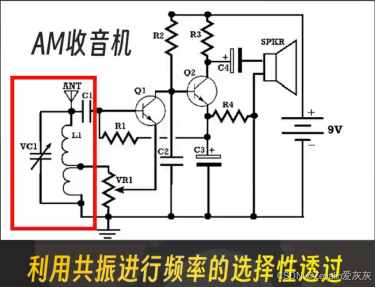
        利用二阶振荡系统的这个特性可以进行选频，如收音机可以选择某个频率的信号，将其接入

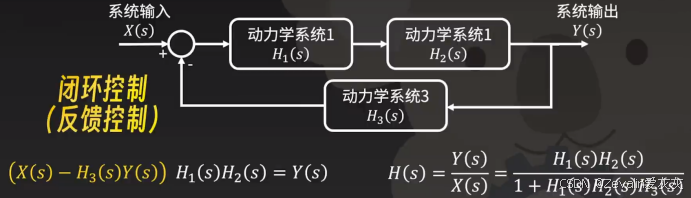
12、传递函数的意义

        传递函数对线性动力学系统进行了极大的计算简化（把时域上的复杂运算转化为频率上简单的加减乘除），从而使得线性系统的级联、反馈等建模成为可能

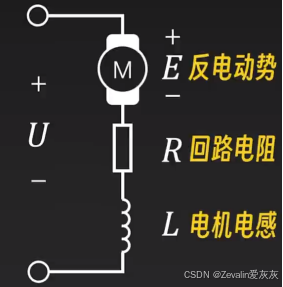
        举个例子，直流电机拖动的动力学系统建模，系统组成如下图所示

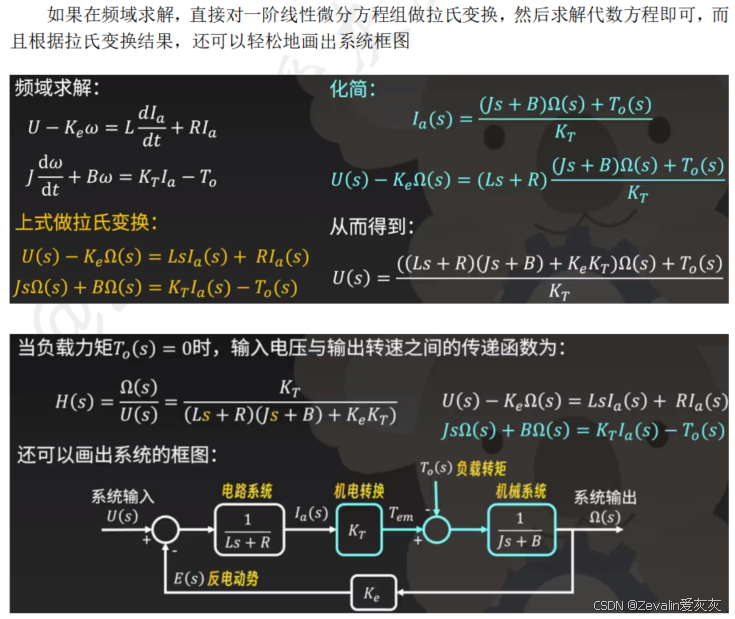
二、闭环控制深入理解

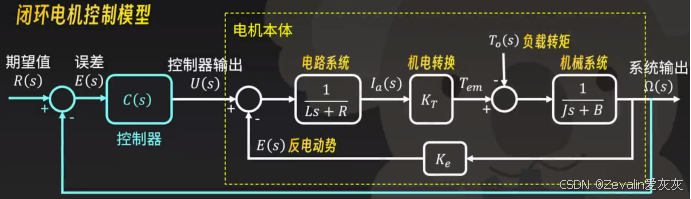
1、闭环反馈环节

        开环的控制系统虽然稳定，但是无法对外界扰动做出反馈，无法进行闭环控制，为了实现闭环控制，需要对系统进行修改，添加反馈环节

        继续以上边的例子介绍，为了实现闭环控制，需要设法采集系统的输出，将期望值与输出值进行比较得到误差，将误差通过控制器处理后输出给驱动器即可

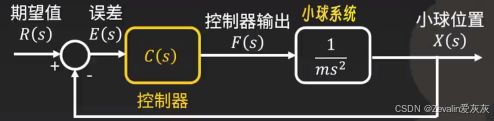
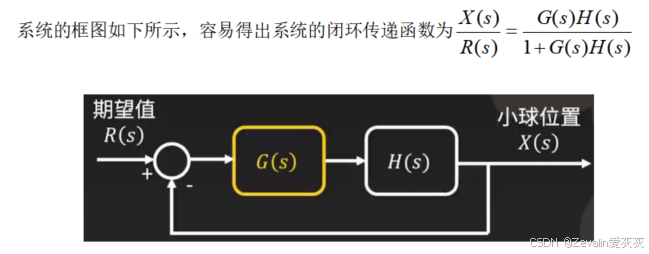
2、小球位置控制模型

        在一个无摩擦的平面上有一个质量为m的小球，需求为控制小球到达平面上的某个特定位置，由于小球不受阻力，因此必须完全依靠改变推力使小球停在给定位置

        基于以上分析，可以设计出小球位置控制系统，其中包括小球系统自身和外接的控制器，控制器根据当前位置和期望位置的误差计算应该对小球施加怎样的力，以控制小球接近目标位置

3、直流电机调速模型

        之前介绍电机是二阶的系统，但由于电感的惯性常常远小于机械的惯性，可忽略电感的惯性环节，将电机视为一阶系统

        电机在运行过程中常常会碰到变负载工况（汽车上坡下坡、机床切削和空走等），为了保证电机在负载状态下的速度稳定，同样可以引入闭环控制

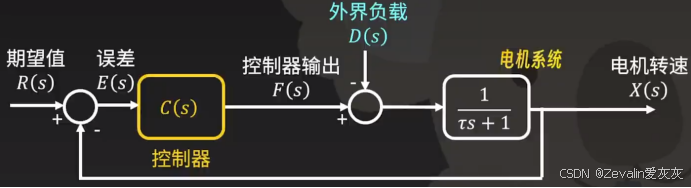
4、PID控制器简介

        通过上述的两个例子，可以得出：

        ①比例控制器（P）为控制器的基础，调节控制器基础响应速度

        ②微分控制器（D）用于控制系统阻尼，减少系统震荡

        ③积分控制器（I）用于消除系统稳态误差和外界干扰的影响

        根据实际需求，可以适当使用PID控制器中的两个（PI、PD）或三个（PID），调节系统响应特性

        PID控制器的优点在于：控制器结构简单、调试简单，不需要对系统的内部有了解