参考教程:
https://www.bilibili.com/video/BV1oz1eYVECp/?spm_id_from=333.1387.favlist.content.click
https://www.bilibili.com/video/BV1uK2mYME36/?spm_id_from=333.1387.favlist.content.click
https://www.bilibili.com/video/BV1XTyTY4EmJ/?spm_id_from=333.1387.favlist.content.click
一、理解卷积
1、离散线性时不变系统通俗理解
(1)系统行为:
①某城市有一个招聘平台。
②每天凌晨两点半,平台投放若干岗位。
③次日凌晨两点半会统计招到的人数以及剩余的空闲岗位数量。
④空闲岗位会继续留在岗位池中等待求职者应聘。
(2)系统规律:
①如果只在第一天投放若干岗位,那么每一天招到的人数(即消耗的岗位数量)是当天空闲岗位数量的60%。
②岗位数量的变化规律和岗位本身数量的多少无关。
③一段时间内,每一天呈现的岗位数量变化规律是一样的。
(3)以上规律说明此系统的输入(投放岗位)和输出(剩余岗位)能够进行线性叠加,且输入输出的关系不随时间变化,因此该系统是一个线性时不变系统。
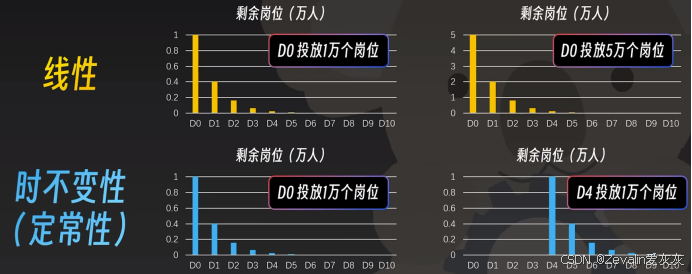
(4)系统的数学模型建立:
①以y[n]表示第n天的空闲岗位数量,可以建立数学模型:
![]()
②以x[n]表示第n天的投放的岗位数量,可以建立数学模型:
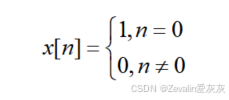
③x[n]与y[n]存在联系,把x[n]输入到系统中,可以计算出y[n],此处的x[n]即冲激函数,在单位冲激函数输入下系统的相应称为冲激响应,即
。
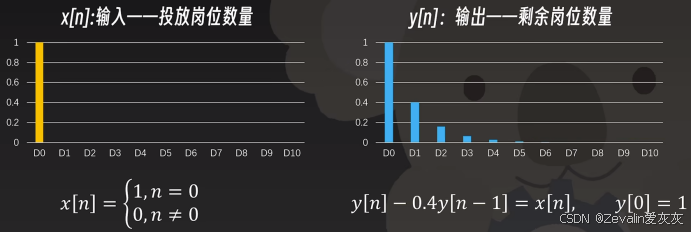
(5)情形代入:
在第0天投放10000个岗位,然后在第4天投放20000个岗位,再在第8天投放5000个岗位,根据情形可以列出如下方程进行求解,得到每天系统输出的剩余岗位数量

输入冲激函数时,系统会有相应的冲激响应输出,对此可以把系统任何不在第0天的输入都视为冲激函数的移位线性组合,于是可以得到x[n]的表达式,根据线性时不变系统性质,每个冲激函数对应一个冲激响应,于是可以得到y[n]的表达式,可见整个系统的输出其实是三个冲激响应输出的叠加

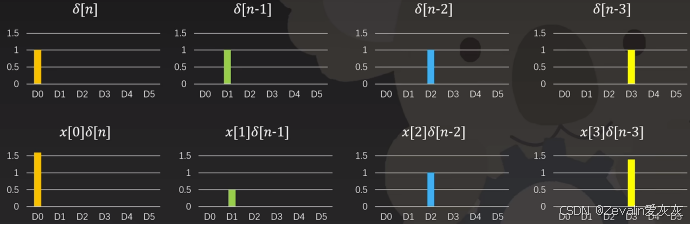
仔细观察求出系统输出的过程,可以得出如下关系式,也就是说,输入信号x[n]是经过线性移位的冲激信号的累加,输出信号y[n]是经过线性移位的冲激响应的累加

如果现在给定每天任意投放的岗位数量x[n],根据上面得出的规律,即可得出离散卷积公式,如下所示
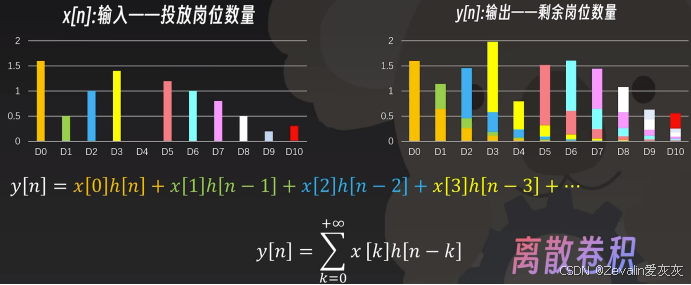
为了便于表达这个式子,将其记为,其中“*”为卷积符号,系统的输出等于系统输入和单位冲激响应的卷积,也就是说,线性系统的冲激相应完全反映了线性系统的特性
仔细观察,可发现冲激函数(包括经过移位的冲激函数)相当于起到了对系统输入筛选提取的作用,由此可见,系统的输入等于其自身和冲激函数的卷积,同时也说明了两点:
①任意函数和冲激函数的卷积等于其自身
②任意函数都可以表示为移位的冲激函数的线性组合
2、连续线性时不变系统通俗理解
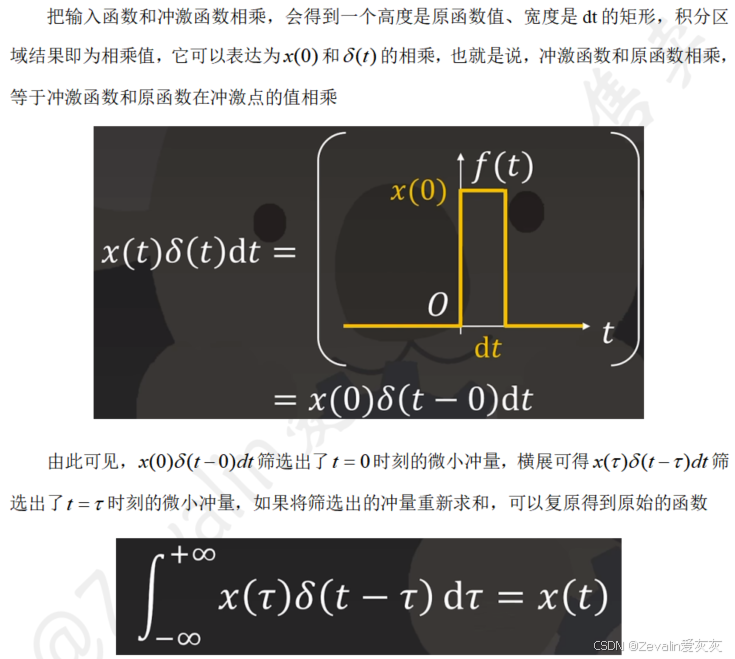
(1)连续时间上的冲激函数的数学表达式是一个函数在0时刻的数值为无穷大,在非0时刻数值均为0,,于是有
,可借助极限的思想进行理解,将函数图像与时间轴形成的积分区域视为宽度无限小、高度无限大的面积为1的矩形,于是引出问题——此面积的意义是什么。
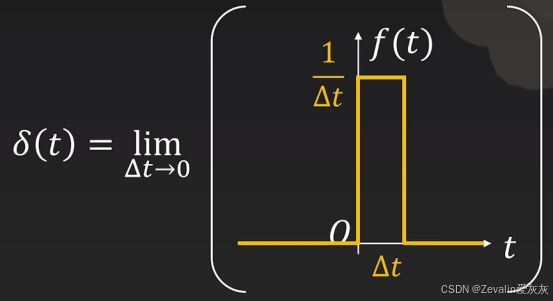
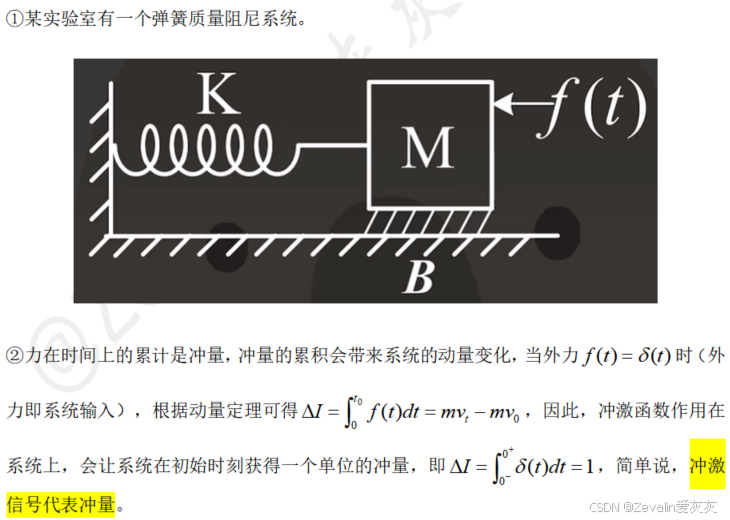
(2)系统行为:
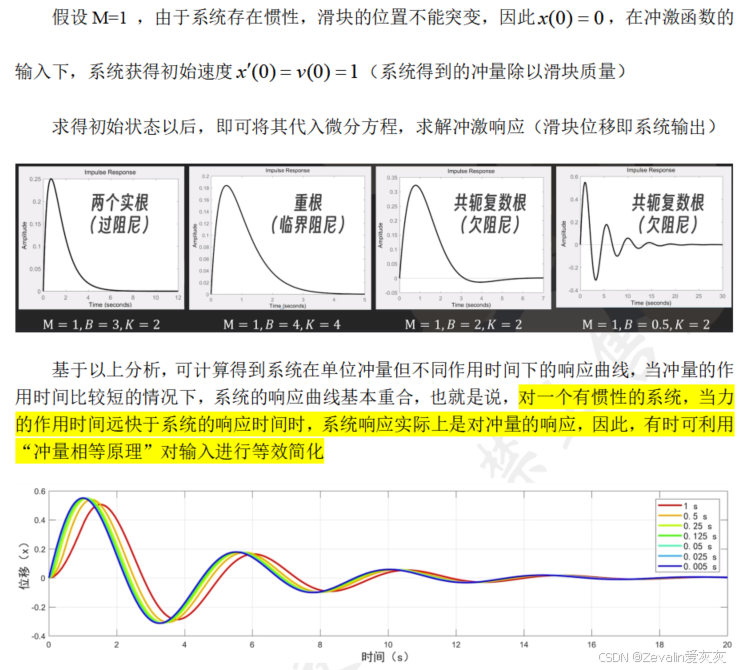
(3)情形代入:
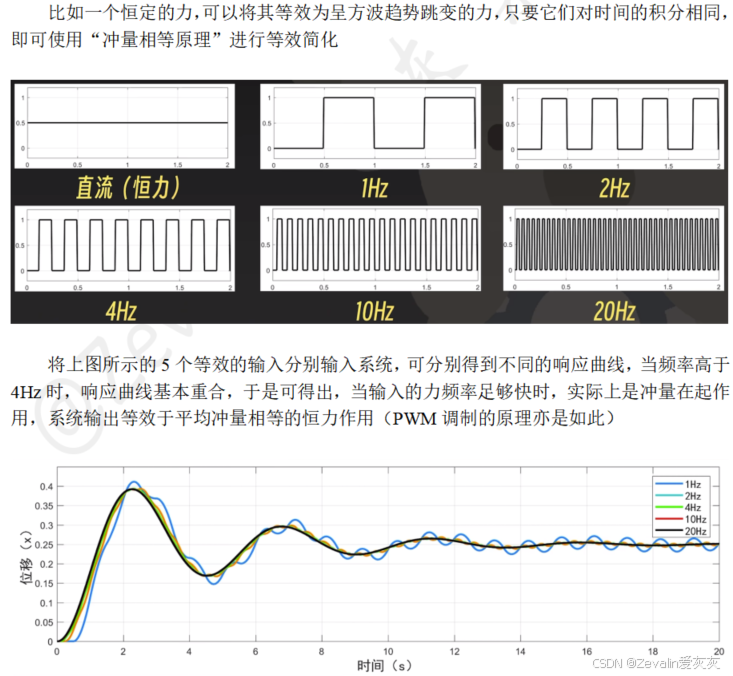

二、理解傅里叶变换
1、前置知识储备——线性代数





2、向量和函数内积的理解

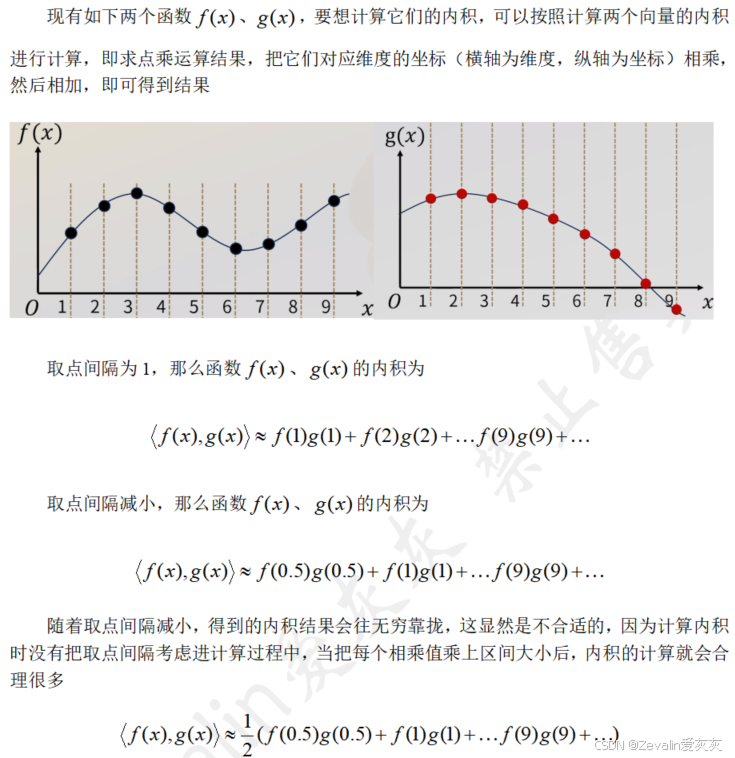
3、积分变换的理解


4、复变函数的内积

5、机电系统微分方程建模

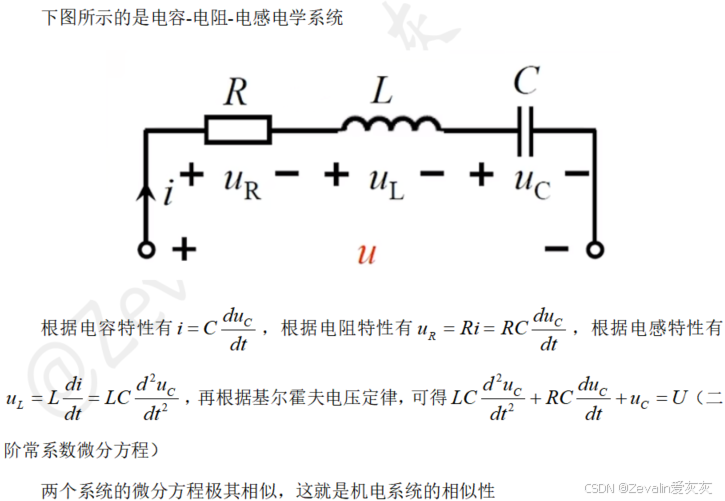
6、微分和积分的矩阵理解
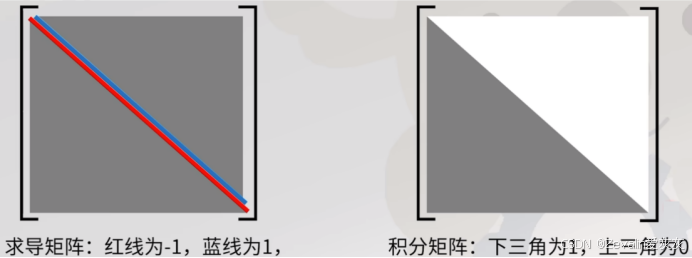
离散的差分就是对一个向量(或者说数列)求后一项和前一项的差,举个例子,假设杭州9月31日起的日最低气温为22℃、17℃、16℃、14℃、17℃、18℃、19℃、18℃、14℃、17℃,要想求每天的最低气温变化差值,可以依次用后一项减前一项而得,这需要列出一条一条的式子,比较麻烦,对此可以考虑用一个有规律的矩阵计算差分(对计算机来说可提高计算速度),如下所示,其中最后一个值-17是一个无效值,因为17℃那天的后一天最低气温无从知晓,只能默认为0℃

从上面的例子中可得知,差分的本质是一个主对角线两侧排满1和-1,其它位置均为0的矩阵
离散的求和就是求一个向量(或者说数列)前n项的和,再举个例子,假设某位同学国庆期间每天的开销分别为85$、200$、160$、100$、60$、75$、50$,要求他这七天的累计开销,可以逐项进行求和,第一项加上第二项求和,再将求和结果加上第三项,以此往复,很显然这也稍微麻烦了一点,对此可以考虑用一个有规律的矩阵计算求和(对计算机来说可提高计算速度),如下所示

从上面的例子中可得知,求和的本质是一个下三角矩阵
继续抽象下去,求导的本质就是在无限密集情况下的差分,积分的本质就是在无限密集情况下求和,再结合之前的推导,差分和求和都是矩阵,而函数的本质是无穷维的向量,那么可以得出,求导和积分的本质是无穷维的矩阵
7、特征向量、求导和积分矩阵的特征函数

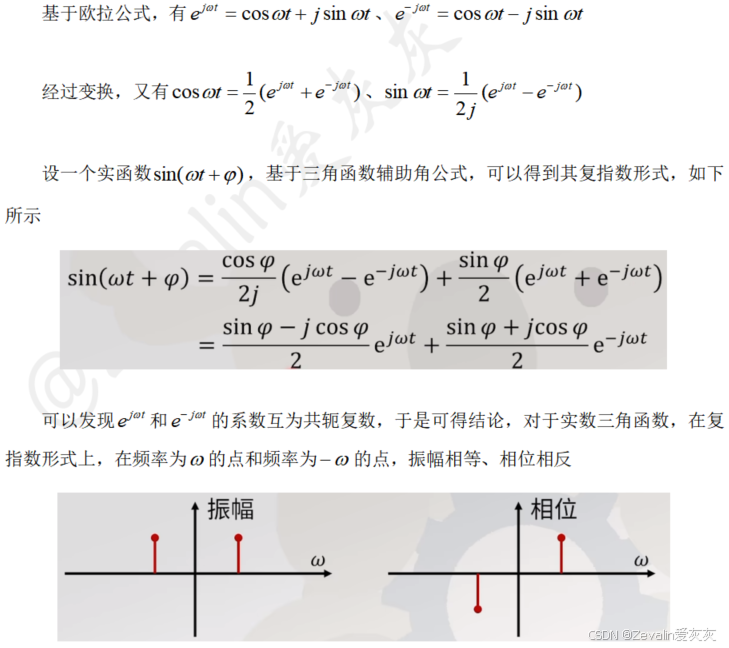
8、三角函数和复指数的关系
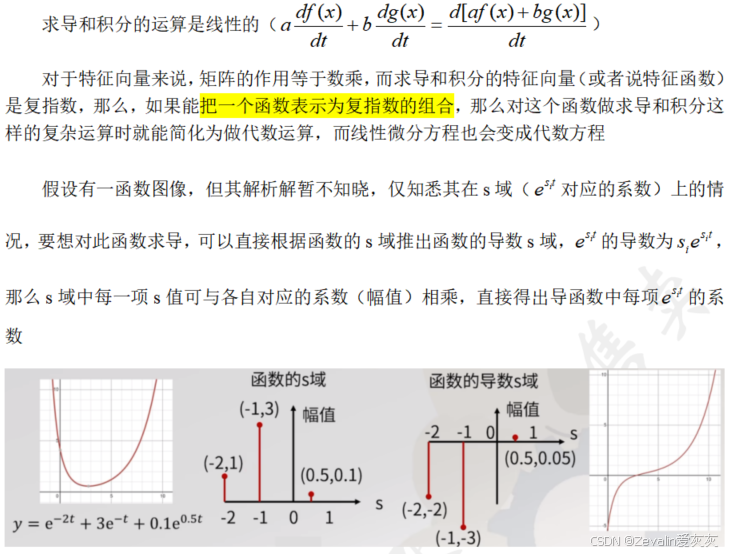
9、复指数做特征向量的应用
10、特征函数解线性微分方程



11、复指数做正交基的前提

12、周期函数的频率分解

13、正弦、余弦基的傅里叶级数

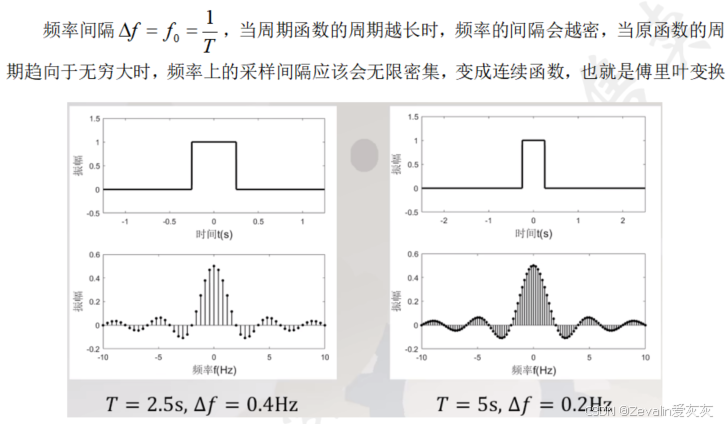
14、傅里叶级数到傅里叶变换
15、傅里叶变换公式推导


16、傅里叶变换和积分变换的对应关系

三、理解拉氏变换
1、MATLAB手搓傅里叶变换
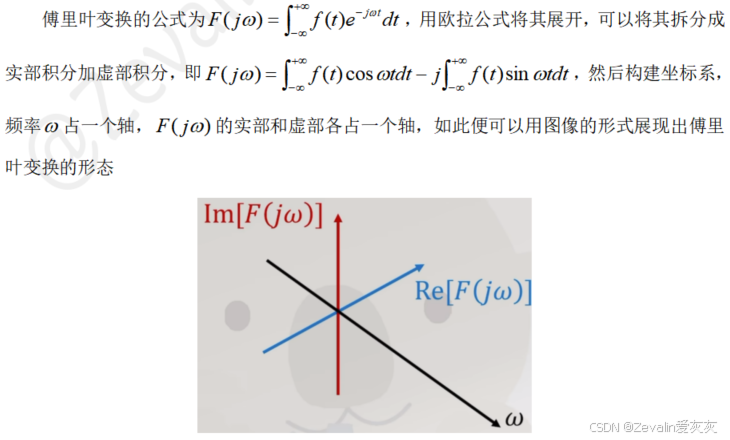
为了让计算机能够计算傅里叶变换,首先需要将连续积分化为数值积分,也即将它们离散化

%创建变量
time = -2:0.001:2;
freq = -10:0.01:10;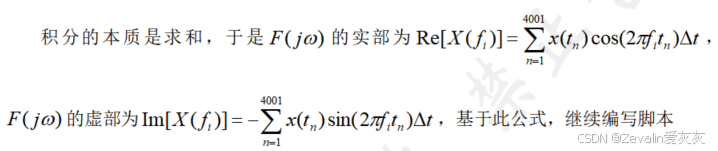
%func为需要做傅里叶变换的函数
func = zeros(1, length(time));
for i = 1501:2501
func(i)=1;
end
%积分运算
FTreal = zeros(1, length(freq));
FTimag = zeros(1, length(freq));
for i = 1:length(freq)
for n = 1:length(time)
FTreal(i) = FTreal(i)+func(n)*cos(2*pi*freq(i)*time(n))*0.001;
FTimag(i) = FTimag(i)+func(n)*sin(2*pi*freq(i)*time(n))*0.001;
end
end
%绘制频谱图
plot3(freq, FTreal, FTimag, '-k', 'Linewidth', 2);
axis([-10 10 -2 2 -2 2]);
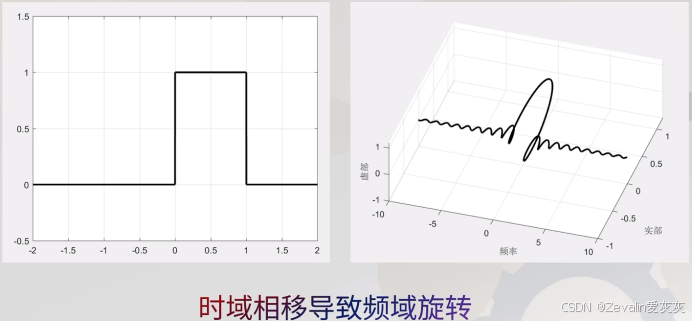
xlabel('频率');ylabel('实部');zlabel('虚部');grid on2、时域频移导致频域旋转
尝试变换几个函数,会发现偶函数的傅里叶变换只有实部,奇函数的傅里叶变换只有虚部
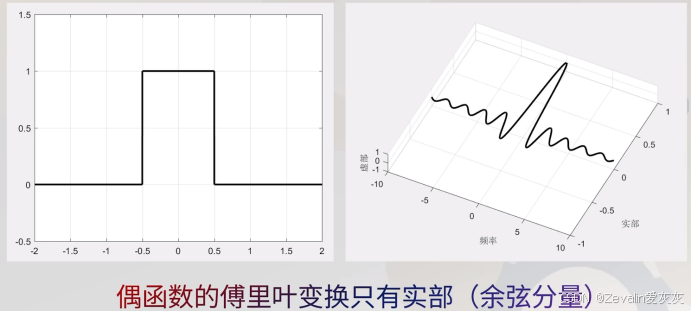
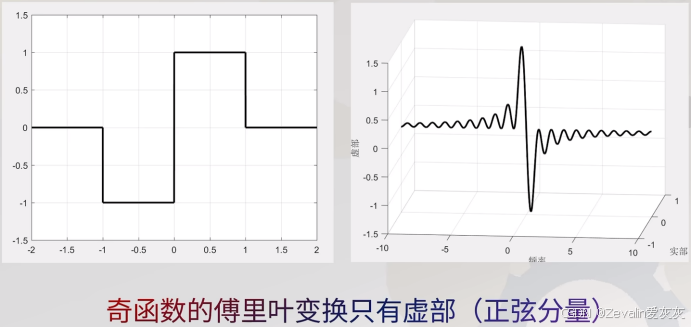
对函数做时域的平移,其频域也会相应地发生旋转
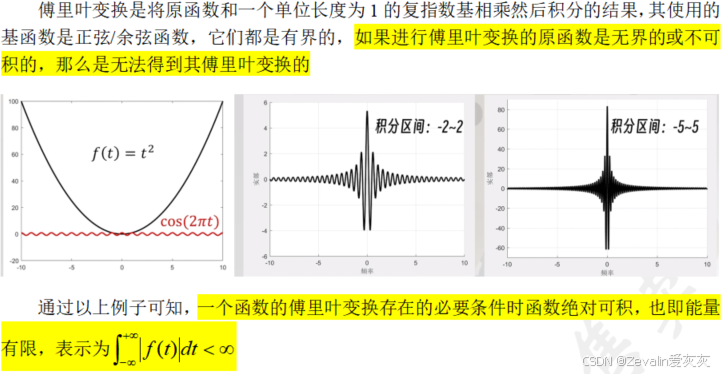
3、傅里叶变换的局限性
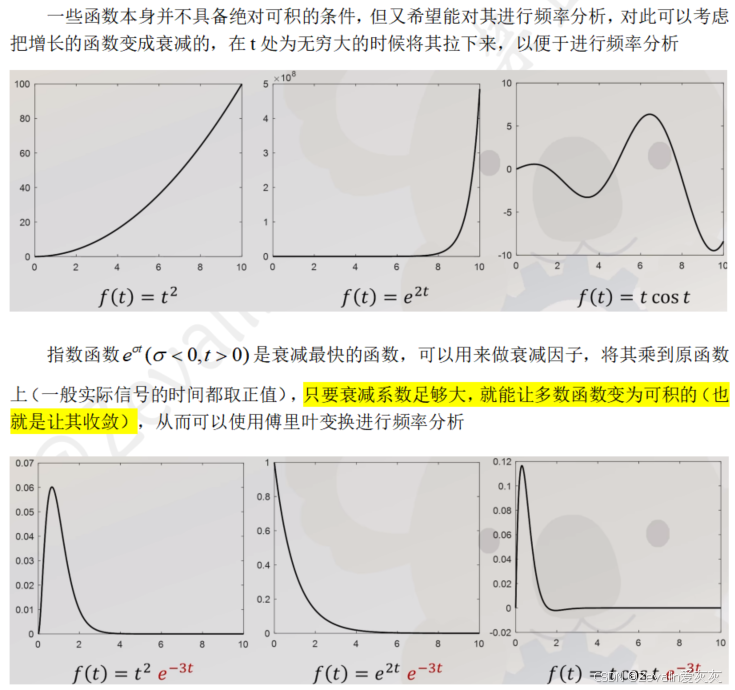
4、拉普拉斯变换公式推导

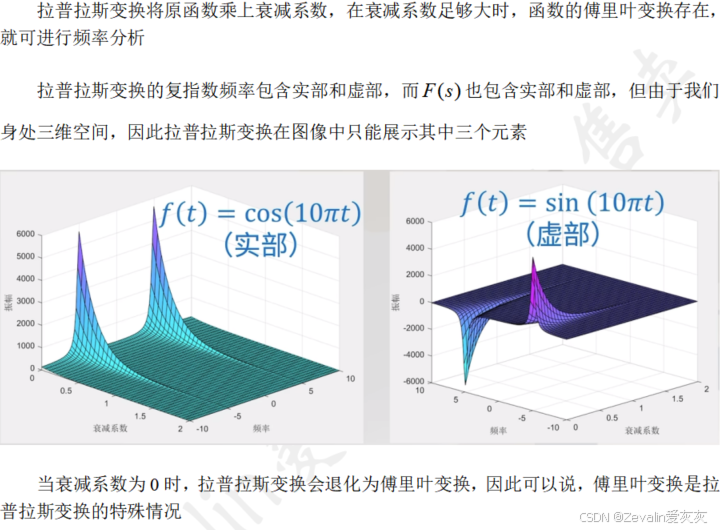
5、拉普拉斯变换的含义
6、拉普拉斯反变换
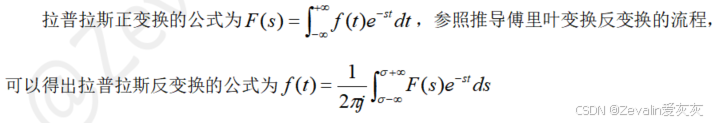
7、常见的拉普拉斯变换公式
一般来说,拉氏变换的原函数都默认会乘上阶跃函数

8、拉普拉斯变换的线性特性
如下为拉普拉斯变换的线性特性,其中线性变换和线性组合的次序可以交换
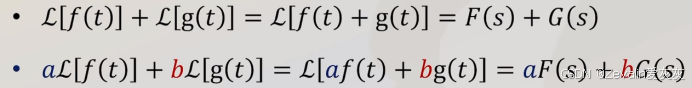
9、拉普拉斯变换的收敛域

10、拉普拉斯变换的微分特性和积分特性
拉普拉斯变换的微分特性和积分特性如下所示,其中求导会去掉函数的初值信息,所以对原函数求导,那么其拉普拉斯变换也要相应地减去中包含的直流分量(也就是常数项C)
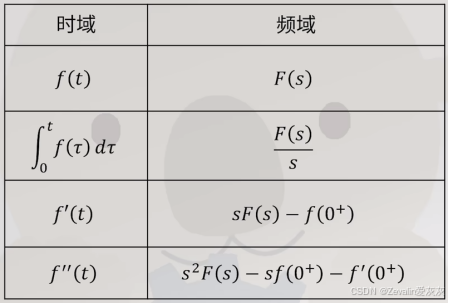
使用复指数基进行积分变换的优势在于能够把求导和积分运算转换为线性运算,从而在需要大量求导和积分的地方简化运算,比如解微分方程、频谱分析、控制系统分析等
10、拉氏变换解线性微分方程
回顾弹簧-质量-阻尼系统模型,其运动受两方面影响,如下所示

因为系统是线性的,所以自由响应和强迫响应可直接进行线性组合,得出来的方程依然是满足的,这也称为全响应,由此也提供了一种解方程的思路,解非齐次线性微分方程,需要先找到自由响应和强迫响应,最后根据初值确定自由响应解的系数
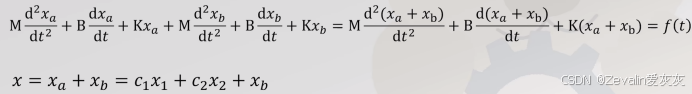




总结一下使用拉氏变换解微分方程流程,将微分方程转化到s域,解s域代数方程,拆分为有理多项式后使用拉氏反变换得到时域解






















 12万+
12万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










