非齐次坐标下的二次曲线
f
(
x
,
y
)
=
0
f(x,y)=0
f(x,y)=0
a
x
2
+
b
x
y
+
c
y
2
+
d
x
+
e
y
+
f
=
0
ax^2+bxy+cy^2+dx+ey+f=0
ax2+bxy+cy2+dx+ey+f=0
进行齐次坐标变换
x
=
x
1
x
3
,
y
=
x
2
x
3
x=\frac{x_1}{x_3},y=\frac{x_2}{x_3}
x=x3x1,y=x3x2得到:
a x 1 2 + b x 1 x 2 + c x 2 2 + d x 1 x 3 + e x 2 x 3 + f x 3 2 = 0 二 次 型 : x T C x = 0 , 其 中 C 是 确 定 曲 线 的 关 键 ( 其 中 C 为 对 阵 矩 阵 C T = C ) 。 ax_1^2+bx_1x_2+cx_2^2+dx_1x_3+ex_2x_3+fx_3^2=0\\ 二次型:x^TCx=0,其中C是确定曲线的关键\\ (其中C为对阵矩阵C^T=C) 。\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ ax12+bx1x2+cx22+dx1x3+ex2x3+fx32=0二次型:xTCx=0,其中C是确定曲线的关键(其中C为对阵矩阵CT=C)。
对偶二次曲线
1.1 以下方程表达的是,二次曲线C上一点x处的切线是Cx。
观
察
形
式
x
T
C
x
=
0
,
记
x
T
C
为
l
,
l
T
x
=
0
,
可
表
达
为
点
在
线
上
l
(
l
T
=
x
T
C
,
l
=
C
T
x
=
C
x
)
观察形式x^TCx=0,记x^TC为l,l^Tx=0,可表达为点在线上l\\ (l^T=x^TC,l=C^Tx=Cx)\\
观察形式xTCx=0,记xTC为l,lTx=0,可表达为点在线上l(lT=xTC,l=CTx=Cx)
1.2
所以二次曲线有两种表达方式,一是满足某二次方程的点
x
T
C
1
x
=
0
x^TC_1x=0
xTC1x=0,另一种是过点的切线l=Cx包络
l
T
C
2
l
=
0
,
其
中
C
2
=
C
1
∗
l^TC_2l=0,其中C_2=C_1^*
lTC2l=0,其中C2=C1∗
退化的二次曲线(二次曲线退化为两条直线)
C = l m T + m l T , r a n k ( C ) = 2 可 以 证 明 : l 上 的 点 l T x = 0 , 满 足 x T C x = 0 ( m 同 理 ) C=lm^T+ml^T,rank(C)=2\\ 可以证明:l上的点l^Tx=0,满足x^TCx=0(m同理) C=lmT+mlT,rank(C)=2可以证明:l上的点lTx=0,满足xTCx=0(m同理)
退化的对偶
二
次
曲
线
C
∗
=
x
y
T
+
y
x
T
,
表
示
由
一
切
过
点
x
或
y
的
直
线
组
成
二次曲线C^*=xy^T+yx^T,表示由一切过点x或y的直线组成\\
二次曲线C∗=xyT+yxT,表示由一切过点x或y的直线组成
1.1 相似变换保对偶二次曲线:
对于退化对偶二次曲线的相似变换
r
a
n
k
(
C
∗
)
=
2
,
H
C
∗
H
T
=
C
∗
,
保
持
不
变
rank(C^*)=2,H C^* H^T=C^*,保持不变
rank(C∗)=2,HC∗HT=C∗,保持不变
1.2 相似变换保角度:
由
此
可
将
两
直
线
的
夹
角
写
成
二
次
曲
线
的
形
式
:
由此可将两直线的夹角写成二次曲线的形式:
由此可将两直线的夹角写成二次曲线的形式:
c
o
s
θ
=
l
1
m
1
+
l
2
m
2
(
l
1
2
+
l
2
2
)
(
m
1
2
+
m
2
2
)
⇒
c
o
s
θ
=
l
T
C
∞
∗
m
(
l
T
C
∞
∗
l
)
(
m
T
C
∞
∗
m
)
cos\theta = \frac{l_1m_1+l_2m_2}{\sqrt{(l_1^2+l_2^2)(m_1^2+m_2^2)}} \Rightarrow cos\theta = \frac{l^TC^*_\infty m}{\sqrt{(l^TC^*_\infty l)(m^TC^*_\infty m)}}
cosθ=(l12+l22)(m12+m22)l1m1+l2m2⇒cosθ=(lTC∞∗l)(mTC∞∗m)lTC∞∗m
验 证 角 度 不 变 性 质 ( 相 似 变 换 ) l T C ∞ ∗ m = l T H − 1 H C ∞ ∗ H T H − T m = l ′ T C ∗ ′ m ′ 验证角度不变性质(相似变换)\\ l^TC^*_\infty m = l^TH^{-1}HC^*_\infty H^TH^{-T}m = l'^TC^*{'}m' 验证角度不变性质(相似变换)lTC∞∗m=lTH−1HC∞∗HTH−Tm=l′TC∗′m′
虚圆点
二 次 曲 线 a x 1 2 + b x 1 x 2 + c x 2 2 + d x 1 x 3 + e x 2 x 3 + f x 3 2 = 0 当 a = c , b = 0 时 表 示 任 意 圆 , 其 与 ( 1 , 1 , 0 ) 的 交 点 满 足 x 1 2 + x 2 2 = 0 方 程 的 解 为 [ 1 ± i 0 ] , 虚 圆 点 将 欧 式 空 间 中 两 个 正 交 方 向 合 并 到 一 个 复 数 中 [ 1 ± i 0 ] = [ 1 0 0 ] + i [ 0 1 0 ] 二次曲线ax_1^2+bx_1x_2+cx_2^2+dx_1x_3+ex_2x_3+fx_3^2=0\\ 当a=c,b=0时表示任意圆,其与(1,1,0)的交点满足x_1^2+x_2^2=0\\ 方程的解为\begin{bmatrix}1\\ \pm i\\0\end{bmatrix},虚圆点将欧式空间中两个正交方向合并到一个复数中\\ \begin{bmatrix}1\\ \pm i\\0\end{bmatrix}= \begin{bmatrix}1\\ 0 \\0\end{bmatrix}+ i\begin{bmatrix}0\\ 1 \\0\end{bmatrix} 二次曲线ax12+bx1x2+cx22+dx1x3+ex2x3+fx32=0当a=c,b=0时表示任意圆,其与(1,1,0)的交点满足x12+x22=0方程的解为⎣⎡1±i0⎦⎤,虚圆点将欧式空间中两个正交方向合并到一个复数中⎣⎡1±i0⎦⎤=⎣⎡100⎦⎤+i⎣⎡010⎦⎤
虚 圆 点 的 对 偶 二 次 曲 线 为 C = [ 1 0 0 0 1 0 0 0 0 ] 虚圆点的对偶二次曲线为C= \begin{bmatrix}1&0&0\\0&1&0\\ 0&0&0 \end{bmatrix} 虚圆点的对偶二次曲线为C=⎣⎡100010000⎦⎤
参考与其他:
l ∞ = ( 1 , 1 , 0 ) l_\infty =(1,1,0) l∞=(1,1,0)
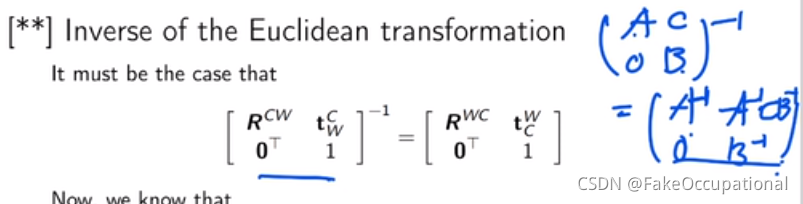
投影变换矩阵的分解:

https://blog.youkuaiyun.com/weixin_34234829/article/details/94312128?
https://blog.youkuaiyun.com/baicaidiaozhui/article/details/86634850?
https://blog.youkuaiyun.com/ncepu_Chen/article/details/105322585
https://www.robots.ox.ac.uk/~dwm/Courses/4CV_2015/index.html
A
H=HaP或P dot Ha
然后只需要找方法推导出无穷远线的位置,一般有三种方法
摄影几何:8dof方法
计算机视觉中的多视图几何 – 2D射影几何与变换 --无穷远直线、虚圆点及其对偶以及恢复图像的仿射性质
【虚圆点_百度百科】https://mbd.baidu.com/ma/s/Mcp2AFpN





 本文探讨了非齐次坐标下二次曲线的齐次坐标变换,展示了如何通过变换将二次曲线转化为二次型,并讨论了对偶二次曲线的概念。退化二次曲线被表示为两条直线,而对偶二次曲线则涉及直线的夹角表示。虚圆点作为一种特殊点,将两个正交方向合并到复数中,其对偶二次曲线为对角矩阵。文章还提到了摄影几何中的无穷远线和虚圆点在几何变换中的角色。
本文探讨了非齐次坐标下二次曲线的齐次坐标变换,展示了如何通过变换将二次曲线转化为二次型,并讨论了对偶二次曲线的概念。退化二次曲线被表示为两条直线,而对偶二次曲线则涉及直线的夹角表示。虚圆点作为一种特殊点,将两个正交方向合并到复数中,其对偶二次曲线为对角矩阵。文章还提到了摄影几何中的无穷远线和虚圆点在几何变换中的角色。

















 2346
2346

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








