【电路笔记 通信】 IQ调制/正交调制 & IQ调制实现（模拟 IQ 调制器+数字 IQ 调制器+RF DAC）+QPSK（4-QAM）/16-QAM

• 16-QAM是一种将4位符号对应到一个幅度与相位都改变的载波曲线，IQ调制能是实现QAM的一种重要发方法，其通过混合不同比例的正弦和余弦而获取想要的曲线
• 类似的IQ调制能实现PSK、FSK、OFDM等等编码。

IQ调制（In-phase and Quadrature modulation，同相与正交调制）

• 在数字调制中，与输入一维信号(AM/PM/FM）并调制到载波上不同，IQ调制 可以调制一个二维的复数信号。

• IQ调制通过把二维数据放到一对正交的基(cos 和 sin)上（更多正交基能承载更多维度的数据并行，同一个频率的正交基就是一个sin和一个cos了）；解调时，再从接收到的调制信号中还原出原始的基带两个分量。

• IQ 调制本质是将基带信号分解为两个正交（90° 相位差）的分量（I 和 Q），分别调制到 cos 和 sin 载波上。将一个复数信号 $s(t)=I(t)+jQ(t)$表示为两个独立的实信号：

  • I分量（In-phase）：与载波同相；
  • Q分量（Quadrature）：与载波正交（相差 90°）。

$$s_{\text{RF}}(t)=I(t)\cdot \cos (2\pi f_{c}t)-Q(t)\cdot \sin (2\pi f_{c}t)$$

• 调整模拟信号的相位不是一件容易的事情，我们可以通过调整振幅 I 和 Q 来控制产生的正弦波的相位和振幅（我们不必调整余弦或正弦的相位），如下面的QPSK所示（图片来自无线通信FPGA设计 (徐文波)）：

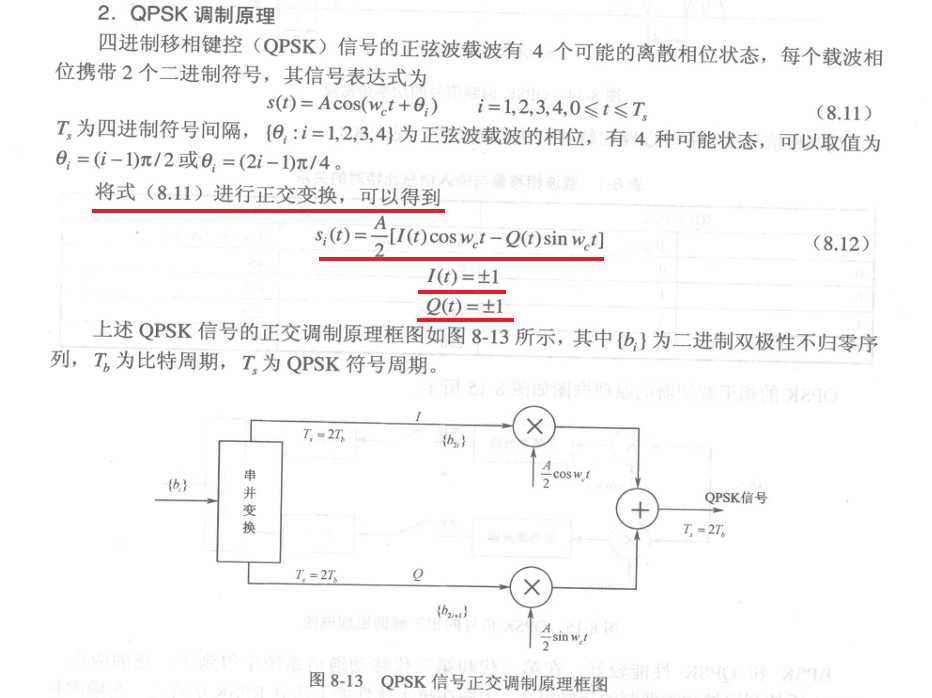
• QPSK, Quadrature Phase Shift Keying(实际也是4QAM）就是最经典的通过 IQ调制 实现的调制方式。

QPSK（4QAM）的符号定义

• 4-QAM有4个符号点，可表示为复平面上的4个点：

比特对	I值	Q值	复平面点 ( I + jQ )	相位
00	+1	+1	( +1 + j1 )	45°
01	-1	+1	( -1 + j1 )	135°
11	-1	-1	( -1 - j1 )	225°
10	+1	-1	( +1 - j1 )	315°

示意图理解

在IQ平面（即复平面）上：

        Q ↑
          |
      *   |   *
          |
  --------+--------→ I
          |
      *   |   *
          |

每个“*”代表一个4QAM符号（星座点）。

• I轴控制信号的“水平分量”
• Q轴控制信号的“垂直分量”
• IQ调制器把它们分别乘以正交载波再相加 → 得到射频信号。

实现方式对比

方式	描述
模拟 IQ 调制器	用混频器 + 90°移相器 + 合成器
数字 IQ 调制器	FPGA/DSP 直接计算并送入 DAC
RF DAC	直接输出调制后的 RF 波形

模拟 IQ 调制器

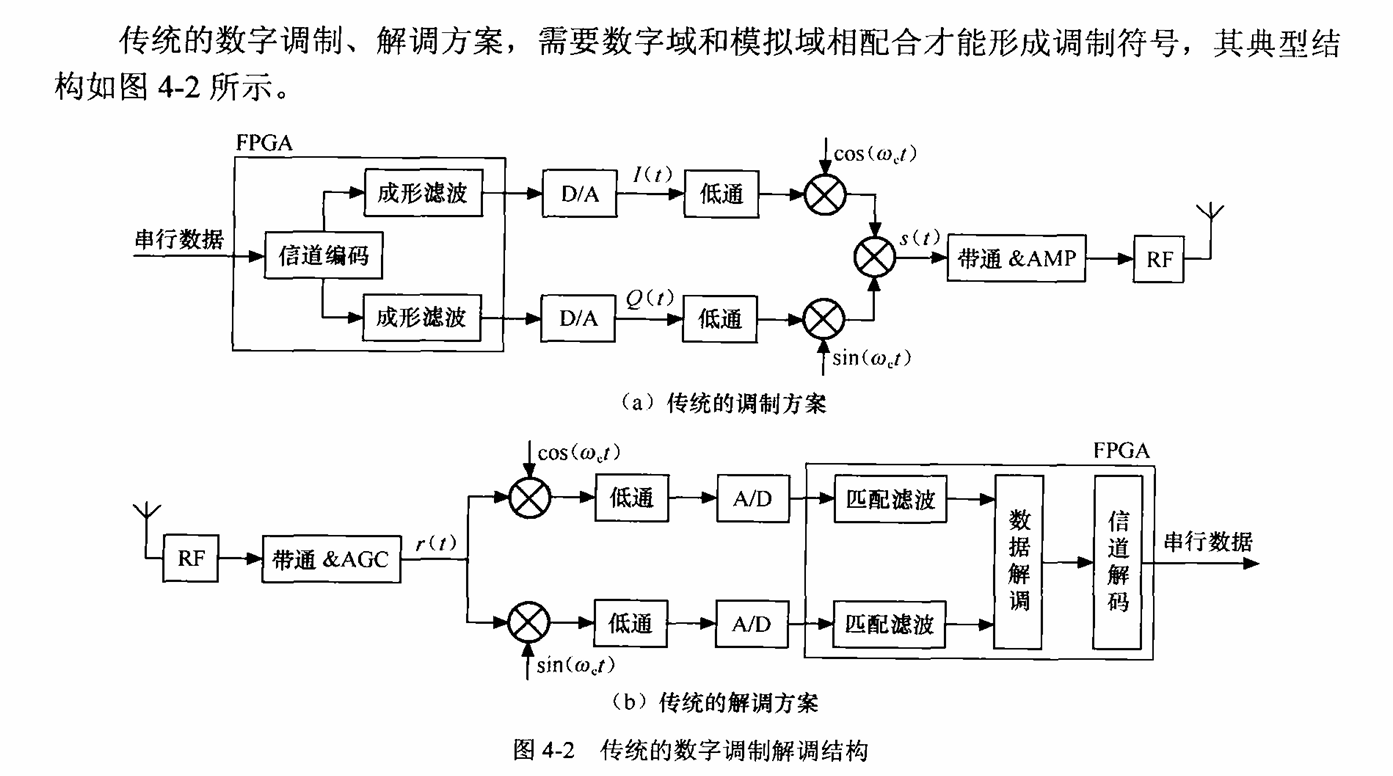
数字 IQ 调制器

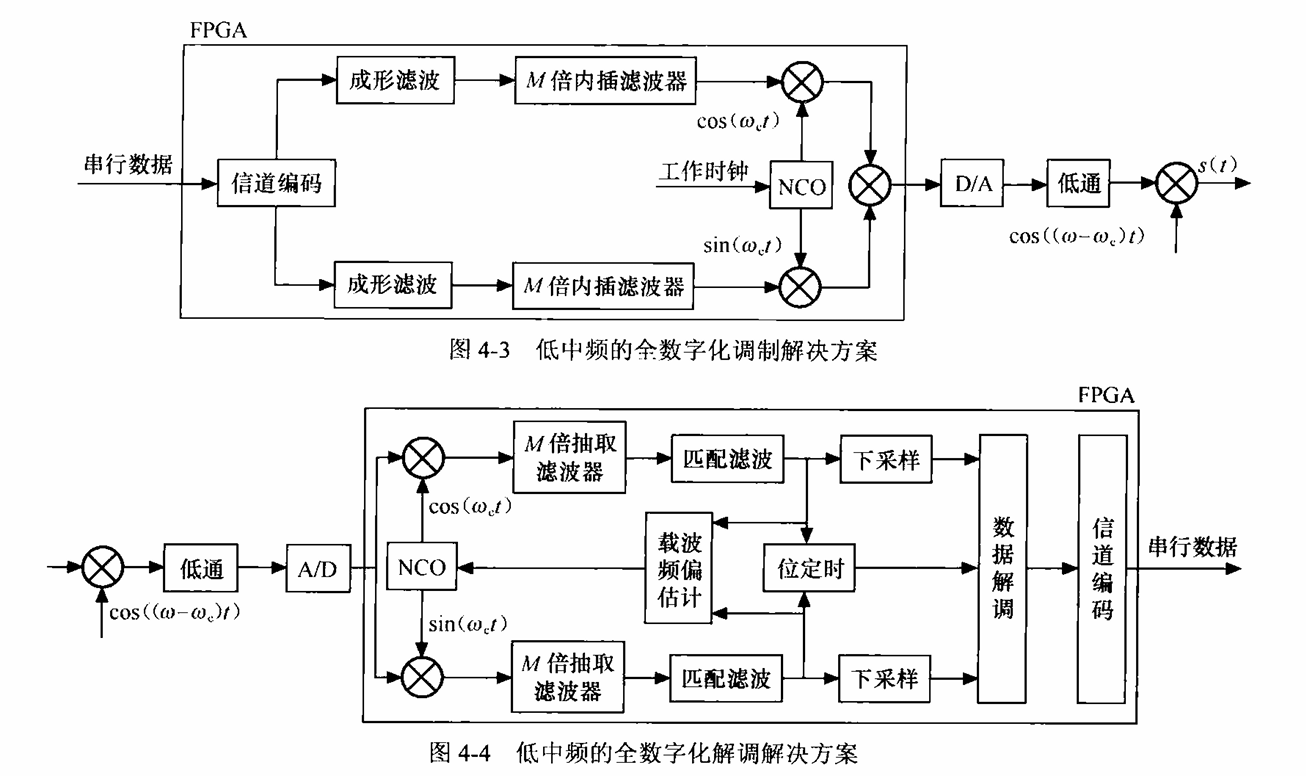
• 数字域，如图4-3所示。比较图4-2（a）可以看出，输出信号只搬移到中低频，这是由于受数字域处理能力和DA速率的限制。·一般要求调制信号的符号速率大于载频点的2倍（因为 DDS的输出速率要大于2倍的频点值），且多为偶数倍。
• 注：两张图片来自无线通信的MATLAB和FPGA实现 (西瑞克斯（北京）通信设备有限公司编著)
  

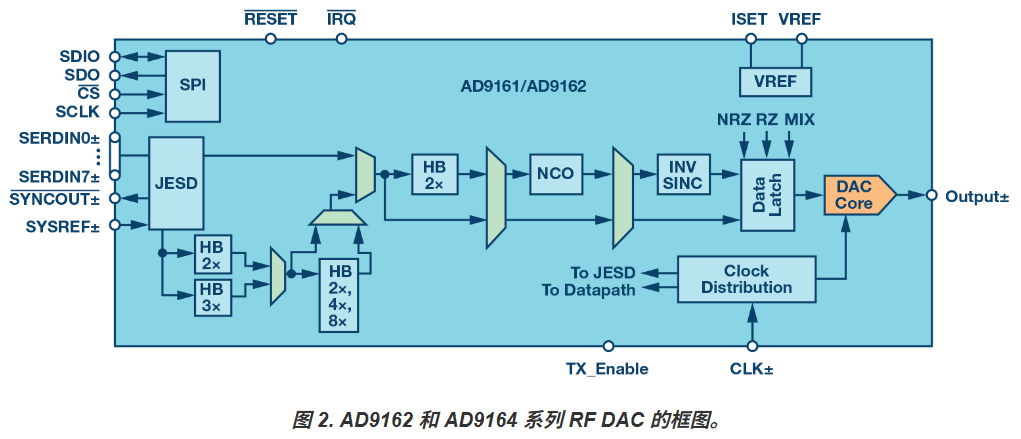
相关器件：RF DAC

• AD9162 和 AD9164 系列射频 DAC 就是一个很好的例子。图 2 显示了 AD9162 和 AD9164 的框图。AD9162 是一款 16 位、6 GSPS 射频 DAC，提供多种插值选项，从 1 倍旁路模式到 24 倍插值。插值器工作在经典的 80% 带宽或更宽的 90% 带宽，以便在略高的功率下获得更大的瞬时信号带宽。数据路径还有一个最终的半带插值器 FIR85，在图 2 中显示为 NCO 之前的“HB 2×”模块，它有效地将 DAC 更新速率翻倍至高达 12 GSPS，从而进一步移动图像并降低滤波要求。可选的 FIR85 之后是一个 48 位数控振荡器 (NCO)，其工作更新速率为 6 GSPS，启用 FIR85 时则为 12 GSPS。NCO 之后是一个 x/sinx 补偿滤波器，通过预加重 DAC 内核的输入来校正 DAC 的 sinx/x 滚降。
  

• I/Q调制器和解调器

更多：QAM-16的示例

• 从 4QAM → 16QAM，我们其实只是在 IQ调制 框架下，把每个符号携带的信息量从 2比特 → 4比特（I/Q 各承载2比特），本质上还是用 同一个IQ调制器实现，只是输入的I、Q电平有更多级。

IQ调制公式（仍然一样）

$$s(t)=I(t)\cos ({\omega }_{c}t)-Q(t)\sin ({\omega }_{c}t)$$

区别仅在于：

• 4QAM：( I, Q \in { +1, -1 } )
• 16QAM：( I, Q \in { +1, +3, -1, -3 } )

也就是说，I/Q 各有 4 个电平，共 4×4=16 个组合 → 16 个星座点。

16QAM 的符号映射表（Gray 编码常用）

比特序列	I值	Q值	星座点
0000	+3	+3	(3, 3)
0001	+1	+3	(1, 3)
0011	-1	+3	(-1, 3)
0010	-3	+3	(-3, 3)
0110	-3	+1	(-3, 1)
0111	-1	+1	(-1, 1)
0101	+1	+1	(1, 1)
0100	+3	+1	(3, 1)
1100	+3	-1	(3, -1)
1101	+1	-1	(1, -1)
1111	-1	-1	(-1, -1)
1110	-3	-1	(-3, -1)
1010	-3	-3	(-3, -3)
1011	-1	-3	(-1, -3)
1001	+1	-3	(1, -3)
1000	+3	-3	(3, -3)

当 Q = 3 时，确实表示在调制信号中，正交载波 的幅度被放大三倍。
从复平面上看，就是信号在 Q 方向上偏得更远，对应更大的垂直分量。