线性代数基础——行列式

最新推荐文章于 2025-06-03 23:12:51 发布

Lonelinessser

最新推荐文章于 2025-06-03 23:12:51 发布

阅读量6.8k

点赞数 17

CC 4.0 BY-SA版权

文章标签：线性代数机器学习人工智能

本文链接：https://blog.youkuaiyun.com/Lonelinessser/article/details/142883931

1.什么是行列式

行列式是一个数学概念，主要用于线性代数中，它是一个可以从方阵（即行数和列数相等的矩阵）形成的一个标量（即一个单一的数值）。

1.二阶行列式

$\begin{vmatrix} a_{11} & a_{12} \\ a_{21}&a_{22} \end{vmatrix}=a_{11}a_{22}-a_{12}a_{21}$

2.三阶行列式

$\begin{vmatrix} a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33} \end{vmatrix}=\begin{matrix} a_{11}a_{22}a_{33}+a_{12}a_{23}a_{31}+a_{13}a_{21}a_{32}& \\ \ -a_{13}a_{22}a_{31}-a_{12}a_{21}a_{33}-a_{11}a_{23}a_{32} & \end{matrix}$

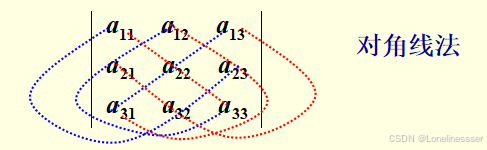
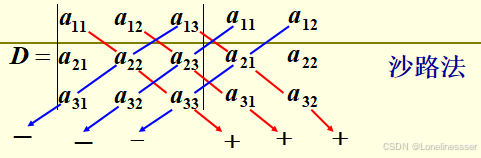
3.n阶行列式

1.排列

由1，2，…，n 组成的一个有序数组，称为一个n级排列，对于一个包含 n 个元素的集合，其所有元素的全排列数目是 n!（即 n 的阶乘）

2.逆序

在一个排列中，如果一对数的前后位置与标准次序相反，即前面的数大于后面的数，则称这对数为一个逆序。

一个排列中逆序的总数称为这个排列的逆序数

注：

1.排列 123 称为标准排列，其逆序数为０

2.排列 $j_1j_2...j_n$ 的逆序数常记为 $N(j_1j_2...j_n)$ 或 $\tau (j_1j_2...j_n)$

3. $N(j_1j_2...j_n)$ = $j_1$ 后面比 $j_1$ 小的数的个数+ $j_2$ 后面比 $j_1$ 小的数的个数+...+ $j_{n-1}$ 后面比 $j_{n-1}$ 小的数的个数.

4. $N(j_1j_2...j_n)$ = $j_2$ 后面比 $j_2$ 大的数的个数+ $j_3$ 后面比 $j_3$ 大的数的个数+...+ $j_{n}$ 后面比 $j_n$ 大的数的个数.

3.奇排列，偶排列

逆序数为奇数的排列称为奇排列；

逆序数为偶数的排列称为偶排列．

标准排列123...n为偶排列

4.对换

把一个排列中某两个数的位置互换，而其余的数不动，得到另一个排列，这一变换称为一个对换

将相邻两个元素对调，叫做相邻对换

性质：

1.对换改变排列的奇偶性，即经过一次对换，奇排列变成偶排列，偶排列变成奇排列

2.所有n级排列中，奇、偶排列各半，均为 $\frac{n!}{2}$

3.任意一个排列与标准排列123...n都可经过一系列对换互换，并且所作对换的次数与这个排列的奇偶性相同

5.n阶行列式

$\begin{vmatrix} a_{11}a_{12}\ldots a_{1n} \\ \vdots \\ a_{n1}a_{n2}\ldots a_{nn} \end{vmatrix}$

等于所有取自不同行不同列的 n 个元素的乘积 $a_{1j_1}a_{2j_2}...a_{nj_n}$ 的代数和，这里 $j_1j_2...j_n$ 为1，2，3...n的排列

每一项 $a_{1j_1}a_{2j_2}...a_{nj_n}$ 都按下列规则带有符号

当 $j_1j_2...j_n$ 为奇排列时带负号

当 $j_1j_2...j_n$ 为偶排列时带正号

$\begin{vmatrix} a_{1}a_{2}\ldots a_{n} \\ \vdots \\ a_{n1}a_{n2}\ldots a_{nn} \end{vmatrix} =\sum _{j_{1}j_{2}\ldots j_{n}}\left( -1\right)^{N\left( j_{1}j_{2}\ldots j_{n}\right) } {a_{1j_{1}}a_{2j_{2}}\ldots a_{nj_{n}}}$

行列式

$\begin{vmatrix} a_{11}a_{12}\ldots a_{1n} \\ \vdots \\ a_{n1}a_{n2}\ldots a_{nn} \end{vmatrix}$

常简记为

$det(a_{ij})$ 或 $\left | a_{ij} \right |$

n级行列式定义展开式中共有n!项

2.行列式的性质

1.行列式的转置，行列式的转置等于行列式本身

$det(A)^T$ 称为 $det(A)$ 的转置

$det(A)^T=det(A)$

其中，A是一个方阵，A^T表示 A 的转置矩阵。

这个性质的证明可以通过行列式的定义和性质来进行。转置行列式的列是行列式的行，即转置行列式按列展开得到的排列和逆序数与行列式按行展开得到的排列和逆序数一样，因此行列式的值保持不变。

2.行列式某行（列）元素的公因子可提到行列式符号之外

$\begin{vmatrix} a_{11} a_{12}\ldots a_{1n} \\ \vdots \\ ka_{s1} ka_{s2}\ldots ka_{sn} \\ \vdots \\ a_{n1} a_{n2}\ldots a_{nn} \end{vmatrix}=k\begin{vmatrix} a_{11} a_{12}\ldots a_{1n} \\ \vdots \\ a_{s1} a_{s2}\ldots a_{sn} \\ \vdots \\ a_{n1} a_{n2}\ldots a_{nn} \end{vmatrix}$

或者说，以一数乘行列式的一行（列）就相当于用这个数乘此行列式。

推论：行列式中某一行（列）为零，则行列式为零

3.若行列式的某一行（列）的元素都是两数之和，则行列式可按此行（列）拆成两个行列式之和

$\begin{vmatrix} (a_{11}+b_{11})&(a_{12} + b_{12})&\ldots& (a_{1n}+b_{1n}) \\ a_{11}&a_{12}&\ldots& a_{1n} \\ \vdots \\ a_{n1}&a_{n2}&\ldots& a_{nn} \end{vmatrix}=\begin{vmatrix} a_{11}&a_{12}&\ldots& a_{1n}+\\ a_{11}&a_{12}&\ldots& a_{1n} \\ \vdots \\ a_{n1}&a_{n2}&\ldots& a_{nn} \end{vmatrix}+\begin{vmatrix} b_{11}&+ b_{12}&\ldots& b_{1n})\\ a_{11}&a_{12}&\ldots& a_{1n} \\ \vdots \\ a_{n1}&a_{n2}&\ldots& a_{nn} \end{vmatrix}$

4.如果行列式中有两行（列）相同，那么行列式为0，所谓两行相同指的是两行元素对应都相等

5.行列式中两行（列）成比例，则行列式为0（由性质2、性质4即得）

6.把行列式的某一行（列）的倍数加到另一行（列），行列式不变（由性质3、性质5即得）

7.换行列式中两行（列）位置，行列式反号

说明：

计算行列式时可多次利用行列式的性质把它化为上三角形或下三角形，从而算得行列式的值．

3.余子式，代数余子式

1.余子式：

给定一个 n×n的矩阵 A，其第 i 行第j 列的元素 aij的余子式 Mij是指去掉第i行和第j列后得到的 (n−1)×(n−1) 子矩阵的行列式。

具体步骤如下：

选择元素：选择矩阵 AA 中的一个元素 aij。
构造余子矩阵：去掉矩阵 AA 的第 i 行和第 j 列，得到一个 (n−1)×(n−1) 的子矩阵。
计算行列式：计算这个 (n−1)×(n−1) 子矩阵的行列式，这个行列式就是元素 aij 的余子式 Mij。

余子式的一个重要应用是计算行列式的值。行列式 det⁡(A)可以通过任意一行或一列的元素与其对应的余子式和代数余子式的乘积之和来计算。

2.代数余子式：

给定一个 n×n 的矩阵 A，其第i行第j列的元素 aij 的代数余子式 Cij定义为：

$C_{ij}=(-1)^{i+j}\cdot M_{ij}$

其中，Mij是元素 aij 的余子式，即去掉矩阵 A的第i 行和第 j 列后得到的 (n−1)×(n−1子矩阵的行列式。

具体步骤如下：

选择元素：选择矩阵 A 中的一个元素 aij。
构造余子矩阵：去掉矩阵 A 的第i 行和第 j 列，得到一个 (n−1)×(n−1)的子矩阵。
计算行列式：计算这个 (n−1)×(n−1)子矩阵的行列式，这个行列式就是元素 aij 的余子式 Mij。
计算代数余子式：根据公式
$C_{ij}=(-1)^{i+j}\cdot M_{ij}$
计算代数余子式。

代数余子式的一个重要应用是计算行列式的值。根据拉普拉斯展开定理，行列式 det⁡(A)可以通过任意一行或一列的元素与其对应的代数余子式的乘积之和来计算。

3.拉普拉斯定理

行列式等于它的某一行元素与其代数余子式的乘积之和。

行列式按第i 行展开的公式为：

$det(A)=a_{i1}C_{i1}+a_{i2}C_{i2}+...+a_{in}C_{in}=\Sigma _{j=1}^{n}a_{ij}C_{ij}$

其中，A 是一个 n×n 的矩阵，aij是矩阵 A的第 i行第 j列的元素，Cij是元素 aij的代数余子式。

代数余子式 Cij的定义为：

$C_{ij}=(-1)^{i+j}M_{ij}$

其中，Mij 是元素 aij 的余子式，即去掉矩阵 A 的第 i 行和第j列后得到的 (n−1)×(n−1)子矩阵的行列式。

类似地，行列式也可以按第j列展开：

$det(A)=a_{1j}C_{1j}+a_{2j}C_{2j}+...+a_{nj}C_{nj}=\Sigma _{i=1}^{n}a_{ij}C_{ij}$

通过这种方式，我们可以将一个 n×n 的行列式展开成 n 个 (n−1)×(n−1)的行列式的和，从而简化行列式的计算。

4.克莱姆法则

据克莱姆法则，如果系数矩阵 A 的行列式 det⁡(A)≠0，那么方程组有唯一解，且解 X 的每一个分量 xi可以通过以下公式计算：

$x_{i}=\frac{det(A_i)}{det(A)}$

其中，Ai是将矩阵 A 的第i 列替换为向量 B 后得到的新矩阵。

$A_{i} = \begin{vmatrix} a_{11} & \cdots & b_{1} & \cdots & a_{1n} \\ a_{21} & \cdots & b_{2} & \cdots & a_{2n} \\ \vdots & \ddots & b_{i} & \ddots & \vdots \\ a_{n1} & \cdots & b_{n} & \cdots & a_{nn} \end{vmatrix}$