线性代数（一）-行列式

一、二阶和三阶行列式

1.二阶行列式

PS：只适用于二元线性方程；

2.三阶行列式

 

二、全排列及其逆序数

1.全排列

把n个不同的元素排成一列，叫做这n个元素的全排列；

2.逆序数

对于n个不同的元素，先规定各元素之间有一个标准次序，于是在这n个元素的任一排列中，当某两个元素的先后次序与标准次序不同时，就说有一个一个逆序，一个排列中所有逆序的总数叫做这个排列的逆序数。逆序数为奇数的排列叫做奇排列，为偶数的的排列叫做偶排列；

 

三、n阶行列式的定义

由三阶行列式入手，三阶行列式可以写成

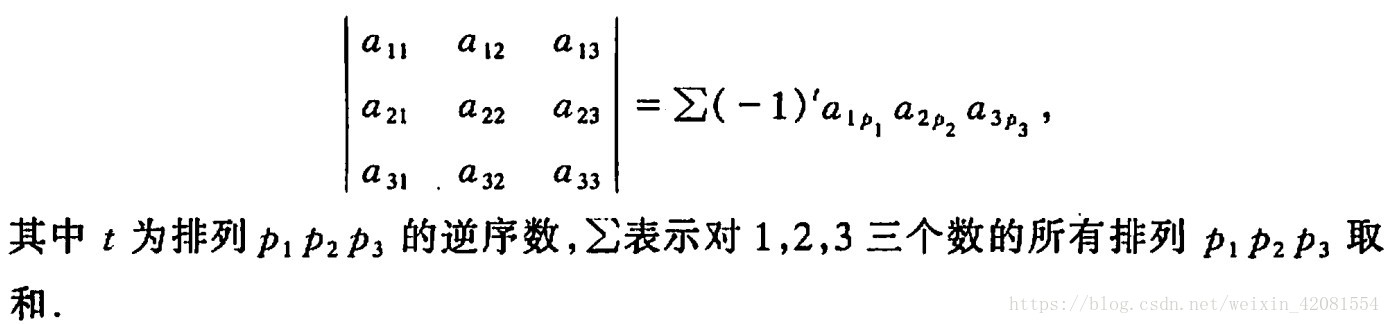
以此类推，可以推广到一般n阶行列式

 

 

 

 

 

 

 

四、对换

在排列中，将任意两个元素对调，其余的元素不动，这种作出新排列的手续叫做对换，将相邻两个元素对换，叫做相邻对换；

1.一个排列中的任意两个元素对换，排列改变奇偶性；

推论：奇排列变成标准排列的对换次数为奇数，偶排列则为偶数；

2.

 

 

 

 

 

五、行列式的性质

 

 

1.行列式和他的转置行列式相等；

2.互换行列式的两行（列），行列式变号；

推论：如果行列式有两行（列）完全相等，则此行列式等于零；

3.行列式的某一行（列）中的所有元素都乘以同一数k，等于用k乘此行列式；

推论：行列式中的某一行（列）的所有元素的公因子可以提到行列式记号的外面；

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

六、行列式按行（列）展开

1.

 

 

 

 

 

 

 

引理:一个n阶行列式，如果其中第i行所有元素除（i，j）元a（ij）外都为零，那么这行列式等于a（ij）与它的代数余子式的乘积，即

 

 

 

 

2.行列式等于它的任一行（列）的各元素与其对应的代数余子式乘积之和，即

这个定理叫做行列式按行（列）展开法则，利用这一法则可以简化行列式的性质；

 七、克拉默法则

1.

 

 

 

 

 

2.如果线性方程组的系数行列式D不等于0，则其一定有解，且解是唯一的；反之，如果方程组无解或有两个不同的解，则它的系数行列式必为零；

3.对于齐次线性方程（即等式右边全为0），如果系数行列式D不等于0，则齐次线性方程组没有非零解；反之，如果有非零解，则系数行列式必为0；