Day 12 启发式算法

最新推荐文章于 2025-11-24 17:02:03 发布

原创最新推荐文章于 2025-11-24 17:02:03 发布 · 1.6k 阅读

12 ·

CC 4.0 BY-SA版权

文章标签：

#启发式算法 #算法

@浙大疏锦行

今日任务：

三种启发式算法的示例代码：遗传算法、粒子群算法、退火算法
学习优化算法的思路（避免浪费无效时间）
以自由探索的思路为主，尝试检索资料、视频、文档，用尽可能简短但是清晰的语言看是否能说清楚这三种算法每种算法的实现逻辑，帮助更深入的理解。

启发式算法介绍

启发式算法是一种问题求解策略，它通过在可接受的计算成本内寻找一个“足够好”的可行解，来替代寻找最优解这一通常非常困难甚至不可能的任务。

具体而言，启发式算法（启发式，意为‘发现’或‘找到’）就像是根据经验、知觉等指引搜索方向，高效地找到较优解；而传统的精确算法则是找到最优，但需要大量的资源和时间。

常见的启发式算法有遗传算法、模拟退火算法、粒子群算法以及蚁群算法等。

遗传算法

灵感来源于达尔文的生物进化论‘物竞天择，适者生存’，生物通过遗传、变异、自然选择，从低级、简单的形态逐步演变为高级、复杂的形态，最终适应环境。

核心思想：将一个待解决的问题转化为一个“环境”，然后生成一群可能的解（称为“种群”），让这些解在模拟的“环境”中竞争、繁衍和进化。经过数代的进化，种群中的“个体”（即候选解）会越来越“适应”环境，也就是越来越接近问题的最优解。

关于遗传算法的术语：

个体：一个候选解。
种群：一组候选解的集合。
染色体：表示一个个体的“基因型”，通常用字符串（二进制、浮点数、符号等）或数据结构表示。它就是对候选解的一种编码。
基因：染色体中的一个元素（位或片段）。
适应度：衡量一个个体好坏的标准，通常由一个适应度函数来计算。适应度越高，个体越优秀，存活和繁衍的机会越大。
选择：根据个体的适应度，从当前种群中挑选出优秀的个体作为父代，用于繁殖下一代。适应度高的个体被选中的概率更大。
交叉：模拟生物的有性繁殖。将两个父代个体的部分染色体进行交换，从而产生新的个体（子代）。这是产生新解的主要手段。
变异：以很小的概率，随机改变个体染色体上的某个或某些基因。这为种群引入了新的遗传物质，增加了多样性，有助于跳出局部最优解。

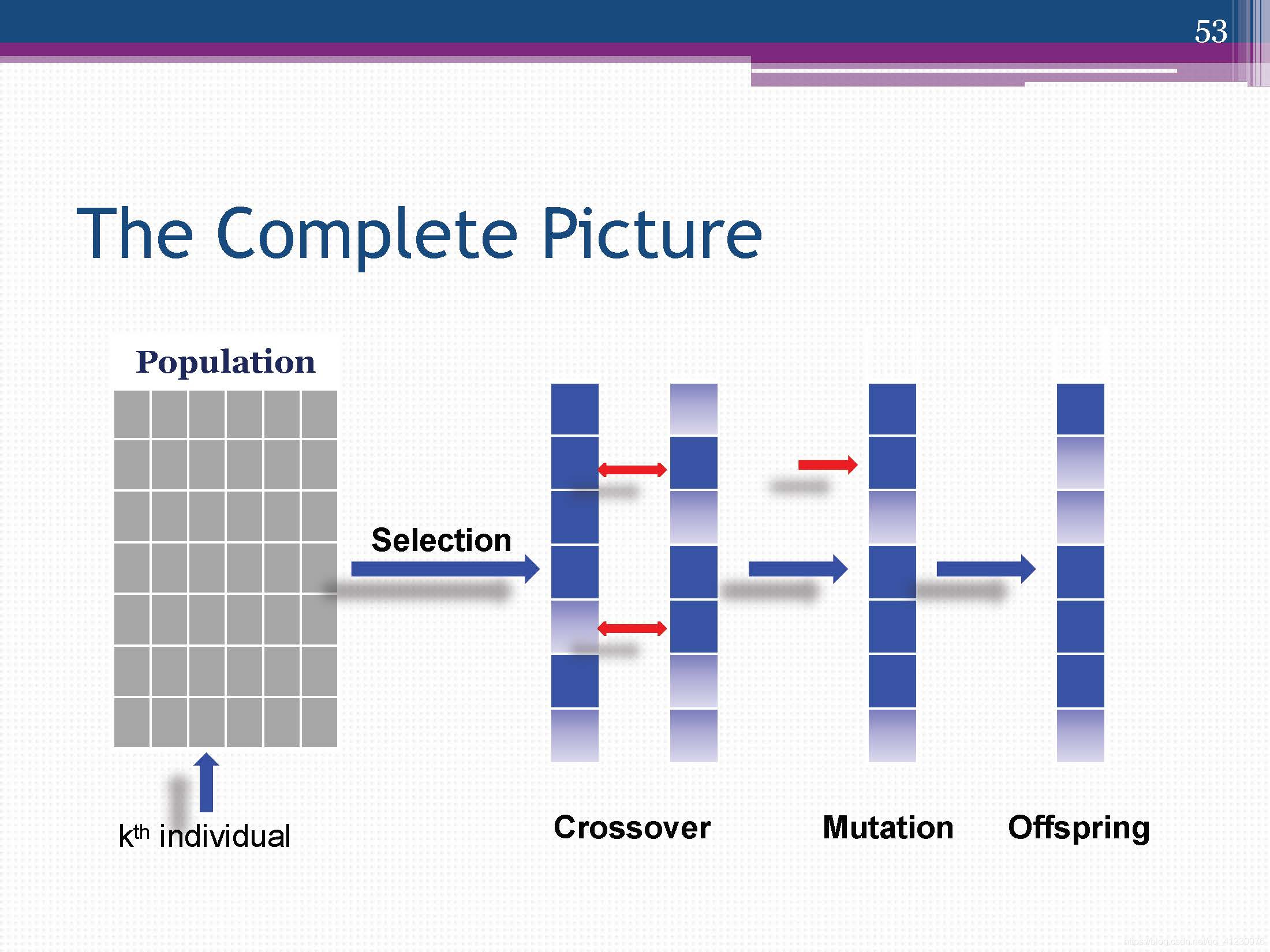
遗传算法简单来说，就是希望通过多次将高质量的个体繁衍后，得到需要的个体，核心操作是选择、交叉、变异。下面为实现逻辑的举例：

初始阶段，对于一个长颈鹿种群来说，内部有脖子长的，也有脖子短的个体。（初始化种群）
而环境中的食物有的在高处，有的在低处。对于脖子长和脖子短的个体，对环境的适应度是不同的。显然，脖子长的个体相较于脖子短的个体获得的食物更多（不考虑其它因素），因此前者的适应能力更强一点。（计算适应度函数进行评估）
对于适应能力更强的长脖子鹿，它们的后代也有更大的概率存活下去。而在这个过程中，个体中也会出现变异的情况。（选择出适应度高的个体作为父代，随机配对选出的父代个体，并以一定的交叉概率交换它们的部分染色体，对交叉后产生的子代种群中的每一个个体，以很小的变异概率随机改变其染色体上的某些基因值。）
树上的果实越来越高，短脖子鹿存活的概率降低。如此循环往复，一代又一代发生进化，最终长脖子鹿就被筛选出来了。（重复以上步骤进行迭代，最终结果趋于稳定）

下面是伪代码（学习自AI）：

// 遗传算法主函数
函数 GeneticAlgorithm:
    输入: 种群大小 pop_size, 最大迭代次数 max_gen, 交叉概率 Pc, 变异概率 Pm
    输出: 最优个体 best_individual
    // 1. 初始化
    当前种群 current_population = 初始化种群(pop_size)
    best_individual = None
    // 2. 主循环
    对于 gen 从 1 到 max_gen:
        // 2.1 评估当前种群
        适应度列表 fitness_scores = []
        对于 每一个个体 individual 在 current_population 中:
            fitness = 计算适应度(individual)
            将 (individual, fitness) 加入 fitness_scores
        // 2.2 更新全局最优解
        current_best = 从 fitness_scores 中找到适应度最高的个体
        如果 best_individual 是 None 或 适应度(current_best) > 适应度(best_individual):
            best_individual = current_best
        // 2.3 检查终止条件 (可选：例如适应度已收敛)
        如果 满足终止条件():
            跳出循环
        // 2.4 选择操作
        父代种群 parents = []
        对于 i 从 1 到 pop_size:
            selected_parent = 选择操作(fitness_scores) // 如轮盘赌选择
            将 selected_parent 加入 parents
        // 2.5 交叉操作
        子代种群 offspring = []
        对于 i 从 0 到 pop_size-1, 步长为 2: // 假设两两配对
            父代1 = parents[i]
            父代2 = parents[i+1]

            如果 随机数(0, 1) < Pc: // 以交叉概率Pc决定是否交叉
                child1, child2 = 交叉操作(父代1, 父代2)
            否则:
                child1, child2 = 父代1, 父代2 // 不交叉，直接复制

            将 child1 和 child2 加入 offspring
        // 2.6 变异操作
        对于 每一个个体 individual 在 offspring 中:
            如果 随机数(0, 1) < Pm: // 以变异概率Pm决定是否变异
                individual = 变异操作(individual)
        // 2.7 种群更替 (用子代完全取代父代)
        current_population = offspring
    // 3. 返回结果
    返回 best_individual
结束函数

遗传算法的核心优势在于强大的全局搜索能力，能够有效处理传统方法难以解决的复杂、非线性及缺乏梯度信息的“黑箱”问题，且对问题数学性质要求低、通用性强。然而，它也存在收敛速度较慢、参数调优敏感、无法保证获得绝对最优解以及编码设计困难等固有局限。

因此，该算法特别适用于传统方法失效的场景，如复杂的组合优化（如路径规划）、机器学习超参数调优、自动设计（如神经网络结构搜索）和多目标优化等问题。当面临一个解空间巨大、多峰值的复杂问题，且对寻找“足够好”的近似全局最优解有需求时，遗传算法是一个极具价值的解决方案。