今日任务:
- 随机种子
- 内参的初始化
- MLP调参:参数分类;调参顺序;各部分调参的调整
作业:对Day 41 的简单CNN 进行调参,看精度是否提高。
随机种子
在代码中很多操作都涉及到随机操作,如内参的随机初始化、数据加载(shuffle打乱)、数据增强操作(随机旋转、缩放等)、dropout等。为了保证每次运行程序时生成的随机数序列相同(实验结果的可重复性),需要设置随机种子。
常见的随机种子有下面四种:
- python内置的随机种子:需要确保random模块、以及一些无序数据结构的一致性
- numpy的随机种子:控制数组的随机性
- torch的随机种子:控制张量的随机性,在cpu和gpu上均适用
- cuDNN(CUDA Deep Neural Network library )的随机性:针对cuda的优化算法的随机性
import torch
import numpy as np
import os
import random
# 全局随机函数
def set_seed(seed=42, deterministic=True):
"""
设置全局随机种子,确保实验可重复性
参数:
seed: 随机种子值,默认为42
deterministic: 是否启用确定性模式,默认为True
"""
# 设置Python的随机种子
random.seed(seed)
os.environ['PYTHONHASHSEED'] = str(seed) # 确保Python哈希函数的随机性一致,比如字典、集合等无序
# 设置NumPy的随机种子
np.random.seed(seed)
# 设置PyTorch的随机种子
torch.manual_seed(seed) # 设置CPU上的随机种子
torch.cuda.manual_seed(seed) # 设置GPU上的随机种子
torch.cuda.manual_seed_all(seed) # 如果使用多GPU
# 配置cuDNN以确保结果可重复
if deterministic:
torch.backends.cudnn.deterministic = True # 使用确定性算法,速度慢但结果精确(可重复)
torch.backends.cudnn.benchmark = False # 关闭基准测试模式,避免自动寻找最优算法
# 设置随机种子
set_seed(42)内参的初始化
回顾简单MLP的训练过程,由于权重通过反向传播来更新,很明显最开始的权重是认为设置的。那么关于参数的初始值,需要清楚它的区间、分布以及数值。
神经网络的对称性
当所有神经元的参数初始值(权重和偏置)完全相同时:
(1)前向传播:对于任何的输入x,经过相同的sigmoid(w*x + b),得到的输出y仍然相同。
(2)反向传播:由于所有神经元的输入、权重、输出都相同,因此得到的损失函数对每个权重的梯度也相同,参数更新后的权重相同。
(3)反复循环,在训练过程中,所有神经元的参数始终相同,相当于只有一个神经元在学习。
随机初始化
因此,不同神经元的参数初始值应该是不一样的,否则会因为MLP的对称性而陷入恶性循环。
使用随机初始化,让初始的神经元各不相同。但是,它们的差异大小是随便控制的吗?
(1)微小的初始差异:非线性函数可能放大微小差异,循环放大后,神经元功能就各异了。
微小初始差异
↓
前向传播产生输出差异
↓
反向传播产生梯度差异
↓
参数更新产生更大差异
↓
......(循环放大)(2)巨大的初始差异:
- 梯度消失或爆炸:sigmoid函数的导数在输入绝对值较大时会趋近于0。输入 x=w・input+b 可能导致激活函数进入 “饱和区”,反向传播时梯度接近 0,权重更新缓慢(梯度消失)
- 训练不稳定:学习过程震荡,梯度变化大
- 收敛困难:初始偏差大,可能陷入局部最优
实际上,通常初始权重设置在接近 0 的小范围内(如 [-0.1, 0.1] 或 [-0.01, 0.01]),或通过特定分布(如正态分布、均匀分布)生成小值。
关于饱和区和非饱和区:

可视化
定义一个简单的CNN模型(1层卷积+1层全连接),然后可视化权重和偏置:
import torch
import torch.nn as nn
import matplotlib.pyplot as plt
import numpy as np
# 设置设备
device = torch.device("cuda:0" if torch.cuda.is_available() else "cpu")
# 定义极简CNN模型(仅1个卷积层+1个全连接层)
class SimpleCNN(nn.Module):
def __init__(self):
super(SimpleCNN, self).__init__()
# 卷积层:输入3通道,输出16通道,卷积核3x3
self.conv1 = nn.Conv2d(3, 16, kernel_size=3, padding=1)
# 池化层:2x2窗口,尺寸减半
self.pool = nn.MaxPool2d(kernel_size=2)
# 全连接层:展平后连接到10个输出(对应10个类别)
# 输入尺寸:16通道 × 16x16特征图 = 16×16×16=4096
self.fc = nn.Linear(16 * 16 * 16, 10)
def forward(self, x):
# 卷积+池化
x = self.pool(self.conv1(x)) # 输出尺寸: [batch, 16, 16, 16]
# 展平
x = x.view(-1, 16 * 16 * 16) # 展平为: [batch, 4096]
# 全连接
x = self.fc(x) # 输出尺寸: [batch, 10]
return x
# 初始化模型
model = SimpleCNN()
model = model.to(device)
# 查看模型结构
print(model)监控权重分布图的作用(实际上可以借助tensorboard监控,避免手动绘制):
- 直观看到其从初始化(如随机分布)到逐渐收敛、形成规律模式的动态变化,理解模型如何一步步 “学习” 特征。
- 识别梯度异常:集中在0附近且更新幅度小,梯度消失;大幅度震荡、超出合理范围,梯度爆炸。
# 查看初始权重统计信息
def print_weight_stats(model):
# 卷积层
conv_weights = model.conv1.weight.data
print("\n卷积层 权重统计:")
print(f" 均值: {conv_weights.mean().item():.6f}")
print(f" 标准差: {conv_weights.std().item():.6f}")
print(f" 理论标准差 (Kaiming): {np.sqrt(2/3):.6f}") # 输入通道数为3
# 全连接层
fc_weights = model.fc.weight.data
print("\n全连接层 权重统计:")
print(f" 均值: {fc_weights.mean().item():.6f}")
print(f" 标准差: {fc_weights.std().item():.6f}")
print(f" 理论标准差 (Kaiming): {np.sqrt(2/(16*16*16)):.6f}")# 改进的可视化权重分布函数
def visualize_weights(model, layer_name, weights, save_path=None):
plt.figure(figsize=(12, 5))
# 权重直方图
plt.subplot(1, 2, 1)
plt.hist(weights.cpu().numpy().flatten(), bins=50)
plt.title(f'{layer_name} 权重分布')
plt.xlabel('权重值')
plt.ylabel('频次')
# 权重热图
plt.subplot(1, 2, 2)
if len(weights.shape) == 4: # 卷积层权重 [out_channels, in_channels, kernel_size, kernel_size]
# 只显示第一个输入通道的前10个滤波器
w = weights[:10, 0].cpu().numpy()
n_shape = w.reshape(-1, weights.shape[2]) # 10个3*3的滤波器重塑为30*3的矩阵
plt.imshow(n_shape, cmap='viridis')
else: # 全连接层权重 [out_features, in_features]
# 只显示前10个神经元的权重,重塑为更合理的矩形
w = weights[:10].cpu().numpy()
# 计算更合理的二维形状(尝试接近正方形)
n_features = w.shape[1] # 4096
side_length = int(np.sqrt(n_features)) # 64
# 如果不能完美整除,添加零填充使能重塑
if n_features % side_length != 0:
new_size = (side_length + 1) * side_length
w_padded = np.zeros((w.shape[0], new_size))
w_padded[:, :n_features] = w
w = w_padded
# 重塑并显示
new_shape = w.reshape(w.shape[0]*side_length,-1) # -1:自动计算列数,10*4096/640=64
plt.imshow(new_shape, cmap='viridis')
plt.colorbar()
plt.title(f'{layer_name} 权重热图')
plt.tight_layout()
if save_path:
plt.savefig(f'{save_path}_{layer_name}.png')
plt.show()
# 打印权重统计
print_weight_stats(model)
# 可视化各层权重
visualize_weights(model, "Conv1", model.conv1.weight.data, "initial_weights")
visualize_weights(model, "FC", model.fc.weight.data, "initial_weights")
# 可视化偏置
plt.figure(figsize=(12, 5))
# 卷积层偏置
conv_bias = model.conv1.bias.data
plt.subplot(1, 2, 1)
plt.bar(range(len(conv_bias)), conv_bias.cpu().numpy())
plt.title('卷积层 偏置')
# 全连接层偏置
fc_bias = model.fc.bias.data
plt.subplot(1, 2, 2)
plt.bar(range(len(fc_bias)), fc_bias.cpu().numpy())
plt.title('全连接层 偏置')
plt.tight_layout()
plt.savefig('biases_initial.png')
plt.show()
print("\n偏置统计:")
print(f"卷积层偏置 均值: {conv_bias.mean().item():.6f}")
print(f"卷积层偏置 标准差: {conv_bias.std().item():.6f}")
print(f"全连接层偏置 均值: {fc_bias.mean().item():.6f}")
print(f"全连接层偏置 标准差: {fc_bias.std().item():.6f}")MLP调参指南
与传统机器学习不同,MLP的基本训练就比较耗时,如果采用之前的网格、贝叶斯等调参方法,那么成本可能有点高。
参数分类
这里介绍的是手动调参方法。参数分为外参和内参,其中外参是实例化手动指定的,也叫超参数。超参数分为三类:
- 网格参数:网络层间的交互、卷积核的数量与尺寸、网络层数和激活函数种类等
- 优化参数:学习率、batch_size、优化器的参数、损失函数的可调参数等
- 正则化参数:权重衰减系数、丢弃比率(Dropout)等
调参顺序
跟学习差不多——及格(60)、拔高(80+)、细节(90+):
“先保证模型能训练(基础配置)→ 再提升性能(核心参数)→ 最后抑制过拟合(正则化)” 的思路,类似 “先建框架,再装修,最后修细节”

下图为整理的调参的思维导图:
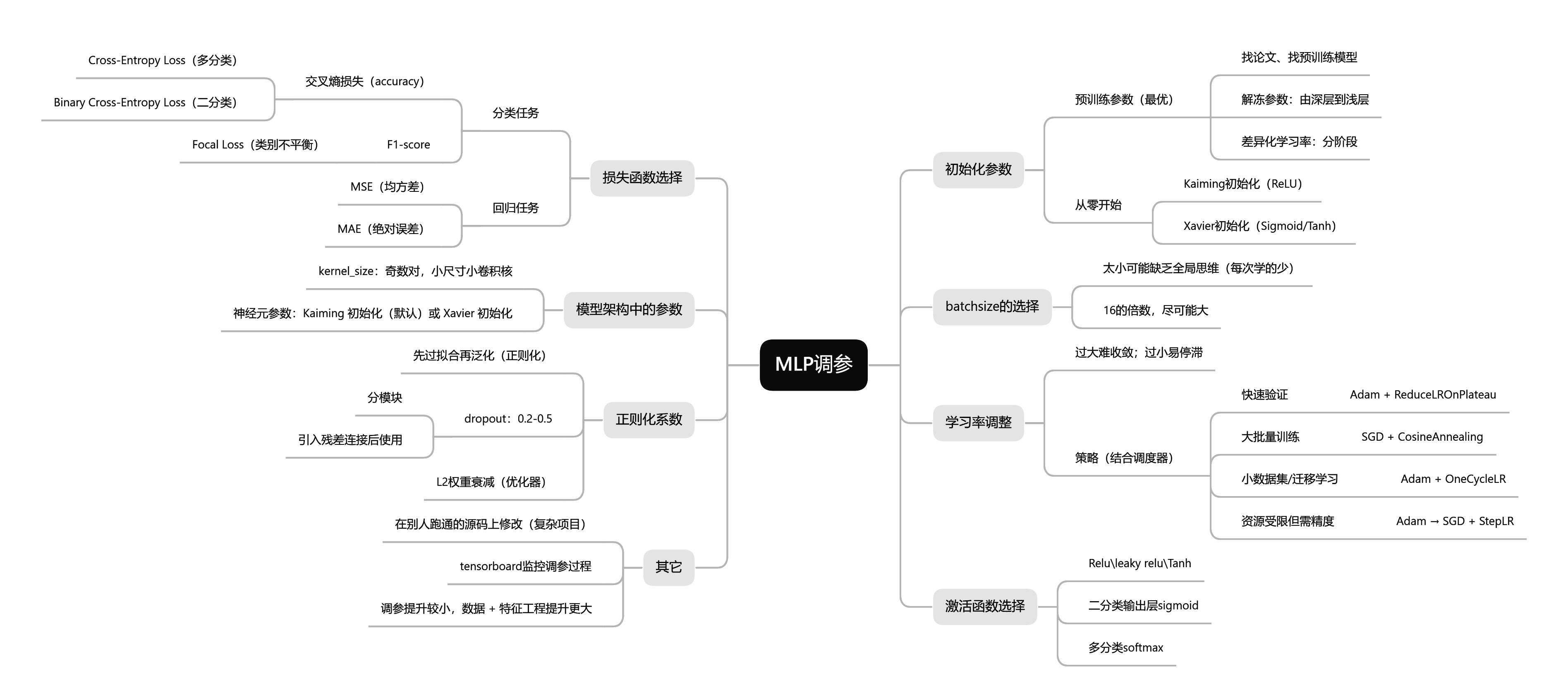
作业
对Day 41 的简单CNN 进行调参,看精度是否提高。
(1)使用Day 41的默认代码(epoch=30),最终准确率82.14%,当然epoch数有点少,loss没有达到收敛。
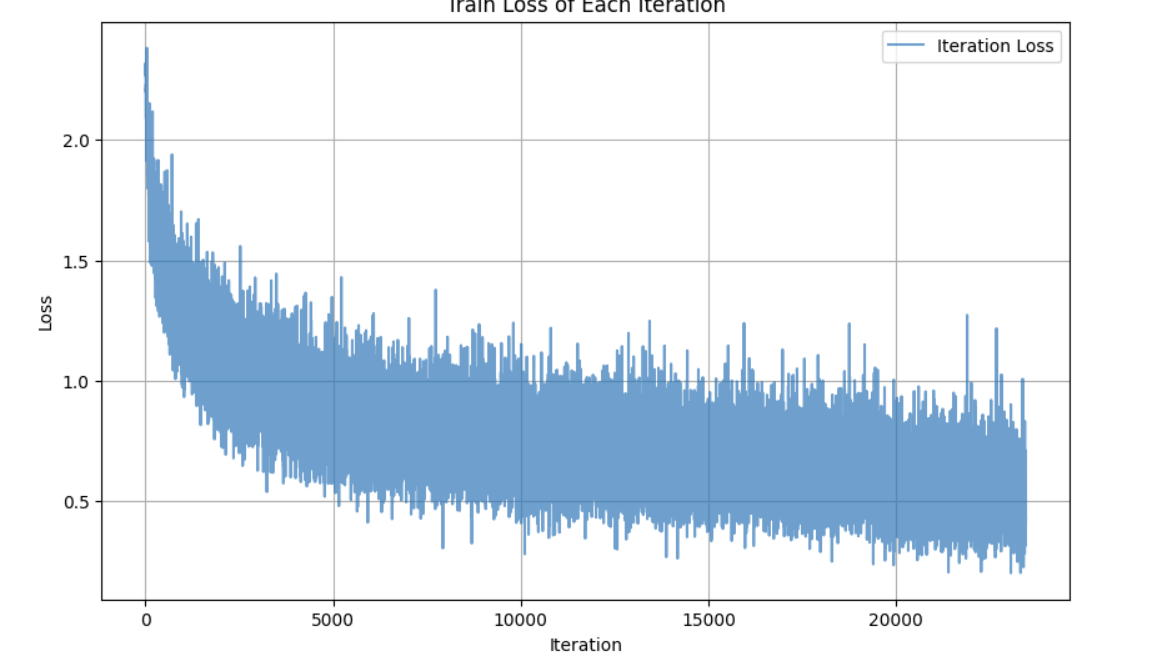
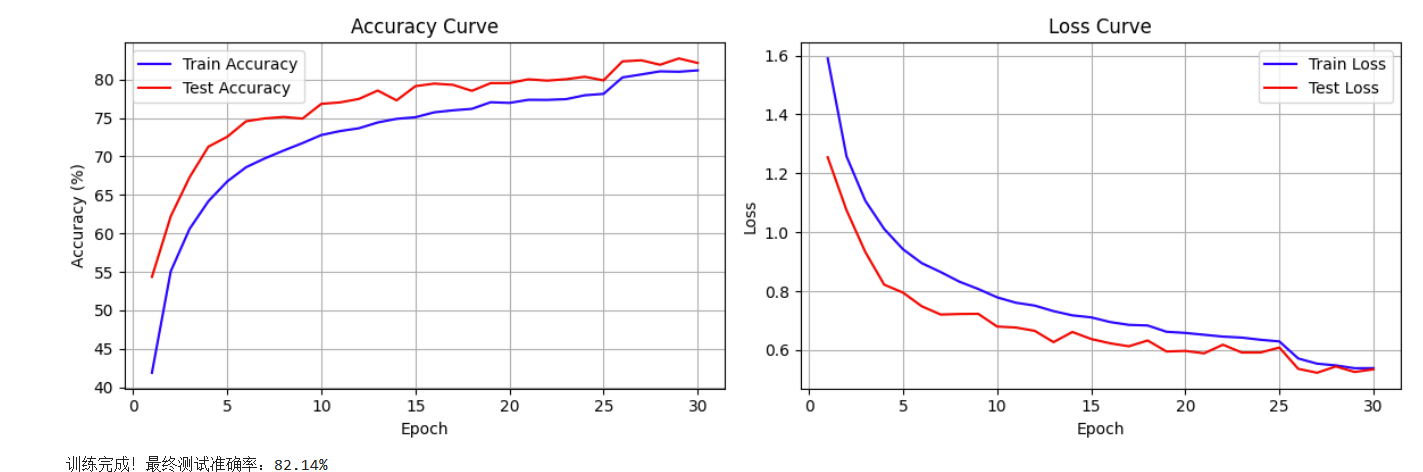
(2)使用Adam → SGD + StepLR 进行优化,epoch=30,加入随机种子。
下面是相较于原来的代码,要做修改的部分:
# 5-训练
def train(model, train_loader, test_loader, criterion, adam_optimizer,sgd_optimizer,scheduler, device, epochs,switch_epoch):
model.train() # 进入训练模式
all_iter_losses = []
iteration_indices = []
train_history_loss = []
train_history_acc = []
test_history_loss = []
test_history_acc = []
for epoch in range(epochs):
epoch_start_time = time.time()
# 优化器的转换:
if epoch < switch_epoch:
optimizer = adam_optimizer
optimizer_name = 'Adam'
else:
optimizer = sgd_optimizer
optimizer_name = 'SGD'
running_loss = 0
total = 0
correct = 0
for batch_idx,(data,target) in enumerate(train_loader):
data,target = data.to(device),target.to(device)
optimizer.zero_grad() # 清零
output = model(data) # 前向传播
loss = criterion(output,target) # 计算损失值
loss.backward() # 反向传播
optimizer.step() # 更新参数
# 存储
loss_value = loss.item()
all_iter_losses.append(loss_value)
iteration_indices.append(epoch*len(train_loader) + batch_idx + 1)
# 统计
running_loss += loss_value
total += target.size(0)
_,predicted = output.max(1)
correct += predicted.eq(target).sum().item()
# 每100个批次打印一次训练信息
if (batch_idx + 1) % 100 == 0:
print(f'Epoch: {epoch+1}/{epochs} | Batch: {batch_idx+1}/{len(train_loader)} '
f'| 单Batch损失: {loss_value:.4f} | 累计平均损失: {running_loss/(batch_idx+1):.4f}')
# 计算
epoch_train_loss = running_loss / len(train_loader)
epoch_train_acc = 100.*correct / total
epoch_test_loss,epoch_test_acc = test(model, test_loader, criterion, device) # 测试集
# 记录历史数据
train_history_loss.append(epoch_train_loss)
train_history_acc.append(epoch_train_acc)
test_history_loss.append(epoch_test_loss)
test_history_acc.append(epoch_test_acc)
# SGD使用调度器
if epoch >= switch_epoch:
scheduler.step()
# 打印准确率
end_time = time.time() - epoch_start_time
current_lr = optimizer.param_groups[0]['lr']
print(f'Epoch {epoch+1}/{epochs} 完成 | 耗时:{end_time:.2f}s | 优化器: {optimizer_name}| LR: {current_lr:.6f}|'
f'| 训练准确率: {epoch_train_acc:.2f}% | 测试准确率: {epoch_test_acc:.2f}%')
# 可视化
plot_iteration_loss(all_iter_losses,iteration_indices)
plot_epoch_metrics(train_history_acc, test_history_acc, train_history_loss, test_history_loss)
return epoch_test_acc
# 8-调用
model = CNN().to(device)
# 损失函数和优化器
criterion = nn.CrossEntropyLoss()
# 设置两个优化器
adam_optimizer = optim.Adam(model.parameters(),lr=0.001)
sgd_optimizer = optim.SGD(model.parameters(),lr=0.01,momentum=0.9,weight_decay=5e-4)
scheduler = optim.lr_scheduler.StepLR(sgd_optimizer,step_size=10,gamma=0.1)
epochs = 30
switch_epoch = 10
print("开始使用CNN训练模型(Adam→SGD + StepLR)...")
final_acc = train(model, train_loader, test_loader, criterion, adam_optimizer,sgd_optimizer,scheduler, device, epochs,switch_epoch)
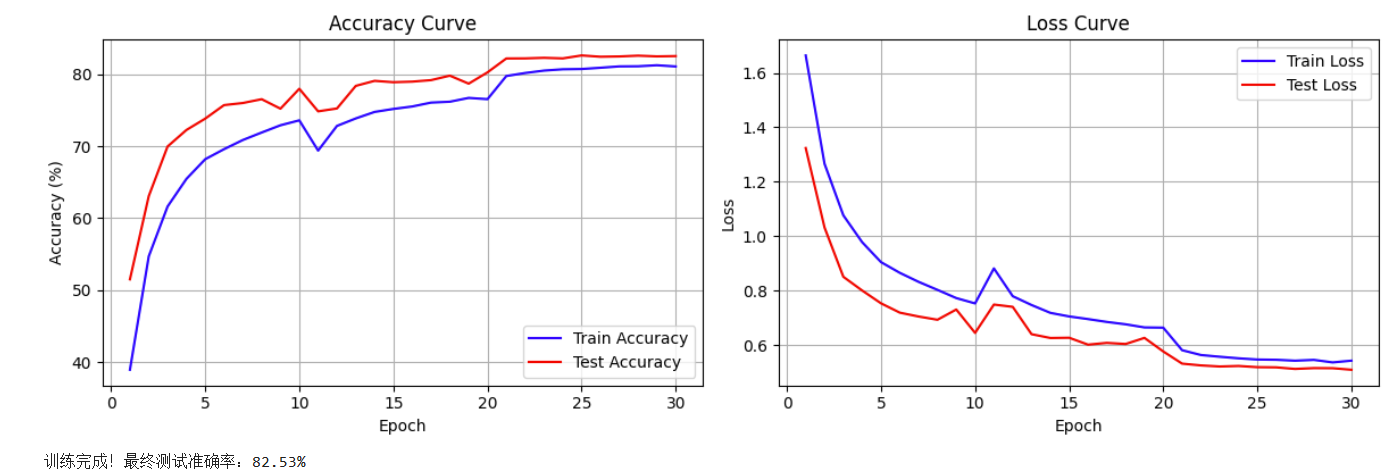
print('训练完成!最终测试准确率:{:.2f}%'.format(final_acc))最终准确率为82.53%。
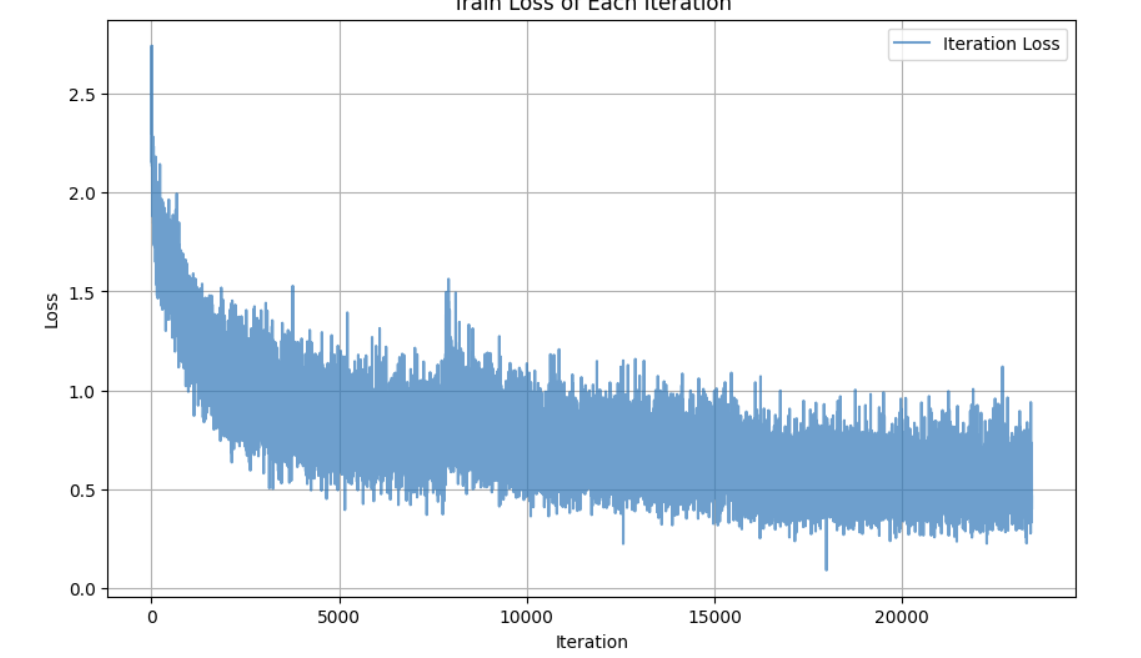
(3)其它:预训练模型(Day44)\早停策略(Day37)





















 920
920

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








